Навигация
Обработка парных сравнений объектов
3.4. Обработка парных сравнений объектов
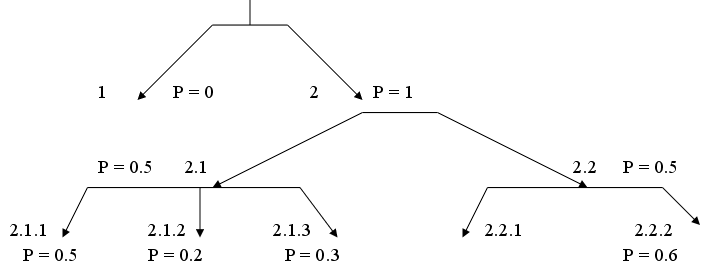
При решении задачи оценки большого числа объектов (ранжирование, определение относительных весов, балльная оценка) возникают трудности психологического характера, обусловленные восприятием экспертами множества свойств объектов. Эксперты сравнительно легко решают задачу парного сравнения объектов. Возникает вопрос, каким образом получить оценку всей совокупности объектов на основе результатов парного сравнения, не накладывая условия транзитивности? Рассмотрим алгоритм решения этой задачи. Пусть m экспертов производят оценку всех пар объектов, давая числовую оценку [12]
(5.36)
Если при оценке пары экспертов высказались в пользу предпочтения экспертов высказались наоборот и экспертов считают эти объекты равноценными, то оценка математического ожидания случайной величины равна [12]
(5.37)
Общее количество экспертов равно сумме
(5.38)
Определяя отсюда и подставляя его в (5.37), получаем [12]
(5.39)
Очевидно, что Совокупность величин образует матрицу на основе которой можно построить ранжировку всех объектов и определить коэффициенты относительной важности объектов.
Введем вектор коэффициентов относительной важности объектов порядка t следующей формулой [12]:
(5.40)
где - матрица математических ожиданий оценок пар объектов, - вектор коэффициентов относительной важности объектов порядка t. Величина равна [12]
(5.41)
Коэффициенты относительной важности первого порядка есть относительные суммы элементов строк матрицы X. Действительно, полагая t=1, из (5.40) получаем [12]
(5.42)
Коэффициенты относительной важности второго порядка (t=2} есть относительные суммы элементов строк матрицы X2 [12].
(5.43)
Если матрица Х неотрицательна и неразложима, то при увеличении порядка величина сходится к максимальному собственному числу матрицы Х [12]
(5.44)
а вектор коэффициентов относительной важности объектов стремится к собственному вектору матрицы X, соответствующему максимальному собственному числу
(5.45)
Определение собственных чисел и собственных векторов матрицы производится решением алгебраического уравнения [12]
(5.46)
где Е—единичная матрица, и системы линейных уравнений [12]
(5.47)
где k – собственный вектор матрицы X, соответствующий максимальному собственному числу . Компоненты собственного вектора есть коэффициенты относительной важности объектов, измеренные в шкале отношений.
С практической точки зрения вычисление коэффициентов относительной важности объектов проще производить последовательной процедурой по формуле (5.40) при t=1, 2, … Как показывает опыт, 3-4 последовательных вычислений достаточно, чтобы получить значения и k, близкие к предельным значениям, определяемым уравнениями (5.46), (5.47).
Матрица неотрицательная, поскольку все ее элементы (5.39) неотрицательны. Матрица называется неразложимой, если перестановкой рядов (строк и одноименных столбцов) ее нельзя привести к треугольному виду [12]
(5.48)
где - неразложимые подматрицы матрицы X. Представление матрицы Х в виде (5.48) означает разбиение объектов на l доминирующих множеств [12]
(5.49)
При 1=n матрица Х неразложима, т. е. существует только одно доминирующее множество, совпадающее с исходным множеством объектов. Разложимость матрицы Х означает, что среди экспертов имеются большие разногласия в оценке объектов.
Если матрица Х неразложима, то вычисление коэффициентов относительной важности позволяет определить, во сколько раз один объект превосходит другой объект по сравниваемым показателям. Вычисление коэффициентов относительной важности объектов позволяет одновременно построить ранжировку объектов. Объекты ранжируются так, что первым объектом считается объект, у которого коэффициент относительной важности наибольший. Полная ранжировка определяется цепочкой неравенств [12]
из которой следует
Если матрица Х является разложимой, то определить коэффициенты относительной важности можно только для каждого множества . Для каждой матрицы определяется максимальное собственное число и соответствующий этому числу собственный вектор. Компоненты собственного вектора и есть коэффициенты относительной важности объектов, входящих в множество . По этим коэффициентам осуществляется ранжировка объектов данного множества. Общая ранжировка объектов дается соотношением [12]
Таким образом, если матрица Х неразложима, то по результатам парного сравнения объектов возможно как измерение предпочтительности объектов в шкале отношений, так и в шкале порядка (ранжирование). Если же матрица Х разложима, то возможно только ранжирование объектов.
Следует отметить, что отношение предпочтения может быть выражено любым положительным числом С. При этом должно выполняться условие В частности, можно выбрать С=2 так, что если , то если то и если , то .
Похожие работы
... элемента на качество принимаемых управленческих решений - одна из главных задач оптимизации процессов принятия решений в управлении общественным производством. Одним из условий преодоления субъективизма при подготовке управленческих решений являются методы исследования операций, методы экспертных оценок. Процедура выработки управленческих решений, являясь сложным логико-мыслительным процессом, ...
... . В ней прежде всего однозначно формулируется подлежащее прогнозу явление, предусматривается в виде гипотиз возможные варианты его исхода. Весьма часто применяется в прикладной социологии и такой метод экспертного прогноза, как “дельфинийская техника”[1]. Он заключается в выработке согласованных мнений путём многократного повторения опроса одних и тех же экспертов. После первого опроса и ...
... осуществляется по следующей формуле: , где , - количество повторений каждого ранга j – м студентом. Практическая работа Здесь осуществляется практическая реализация метода экспертных оценок в анализе качества обучающего процесса в ИП "Стратегия". Этот раздел содержит расчеты показателей, сравнения результирующих данных, факторы, влияющие на показатели. Для получения всех этих данных ...
... Поэтому целесообразно разработать предназначенный для поддержки проведения экспертных исследований АРМ "МАТЭК" ("Математика в экспертизе") на базе РС фирмы "Apple" с использованием современных достижений в области теории и практики экспертных оценок, в области прикладной математической статистики, прежде всего статистики объектов нечисловой природы. Список литературы 1. Орлов А.И. Допустимые ...

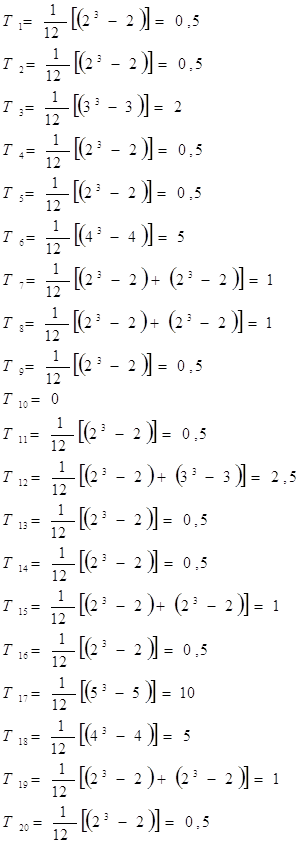
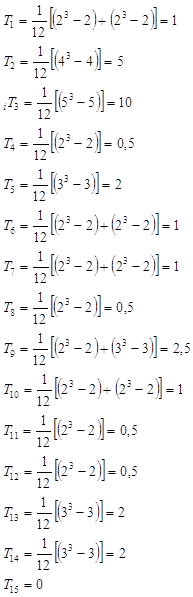
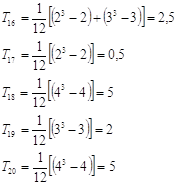
0 комментариев