Содержание темы «Обыкновенные дроби» в школьном курсе математики

1.3. Содержание темы «Обыкновенные дроби» в школьном курсе математики.

Изучение темы «Обыкновенные дроби» в начальной школе.

В соответствии с программой по математике, в начальных классах должна быть проведена подготовка к изучению дробей в IV и V классах. Это значит, в начальных классах надо создать конкретное представление о доле и дроби. С этой целью предусматривается во 2 классе ознакомить детей с долями, их записью, научить сравнивать дроби, решать задачи на нахождение доли числа и числа по доле; в 3 классе ознакомить с дробями, их записью, научить сравнивать дроби, научить решать задачи на нахождение дроби числа. Все названные вопросы раскрываются на наглядной основе.

Ознакомление с долями.

Ознакомить детей с долями - значит сформировать у них конкретные представления о долях, т.е. научить детей образовывать доли практически.

Например, чтобы получить одну четвертую долю круга, надо круг разделить на четыре равные части и взять одну такую часть.

Для формирования правильных представлений о долях надо использовать достаточное количество разнообразных наглядных пособий. Как показал опыт, наиболее удобными пособиями являются геометрические фигуры, вырезанные из бумаги; можно использовать рисунки фигур, выполненные на бумаге или в диапозитивах (круги, прямоугольники, треугольники, бруски, отрезки и т.п.). Очень важно, чтобы пособия были не только у учителя, но и у каждого из учащихся. Правильные представления о долях, а позднее о дробях. Будут сформированы тогда, когда ученики будут своими руками получать, например, половину круга, квадрата, и т.п.

Познакомить детей с долями можно таким образом:

У каждого из учащихся и у учителя по несколько одинаковых кругов, прямоугольников. Возьмите два одинаковых круга. Один из них разделите на две равные части (показывает, как надо перегнуть и как разрезать круг). Это целый круг, а это половина круга, иначе говоря, одна вторая доля круга. Сколько вторых долей в целом круге? (2) . Покажите их. Возьмите квадрат. Как получить одну вторую долю или половину квадрата (разделить его на две равные части и взять одну такую часть)? Выполняйте.

Учащиеся могут сделать это разными способами, например: разрезать квадрат по диагонали и получить два равных треугольника или же разрезать по средней линии, тогда получится два прямоугольника. Некоторые учащиеся могут предложить и другие способы деления квадрата на две равные части (рис.4)

Рис.4

Как получить одну вторую долю круга (разделить круг на две равные части и взять одну такую часть)? Как получили одну вторую долю квадрата? Как иначе называют одну вторую долю круга? Квадрата? (половина –«-,-«-) Сколько половин круга в целом круге (2)?

Доли записывают с помощью двух чисел. Одна вторая доля круга, квадрата обозначается так: 1/2. Число 2 показывает, что круг, квадрат или другая фигура (предмет), разделена на 2 равные части, а число 1 показывает, что взяли одну такую часть.

Учащиеся записывают на половине круга 1/2 и объясняют, что показывает в этой записи каждое число.

Так же образуются доли 1/4, 1/8, 1/3, 1/6, 1/5, 1/10 и др. При этом учащиеся должны уяснить, что для получения например, 1/5 отрезка (прямоугольника, бумажной полоски и т.п.) надо данный отрезок (прямоугольник , полоску и т.п.) разделить на 5 равных частей и взять одну такую часть, что в данном отрезке 5 пятых долей, что одна пятая доля записывается так: 1/5, что в этой записи число 5 обозначает, на сколько равных частей разделен отрезок, а число 1, - что взята одна такая часть. Для закрепления этих знаний и умений учащимся предлагают различные упражнения.

Это прежде всего упражнения в назывании и записи долей (рис.5) Назовите и запишите, какая доля квадрата (круга) отрезана (закрашена).

Рис.5

Можно предлагать самим детям изобразить к.л. долю отрезка и записать эту долю.

В каждом случае надо спрашивать, сколько всего долей в целом. Например, сколько третьих долей отрезка во всем отрезке и т.п.

Эффективным упражнением для формирования представлений о долях является сравнение долей одной и той же величины, которое выполняется чисто практически, с помощью наглядных пособий.

Например, предлагается сравнить доли 1/3 и 1/2 и поставить знак “>”, ” “ , “ < “ или “ = “

3/8*3/4 ; 4/5*1 ; 4/8*1/2 ;

Подбираете такое число, чтобы равенство (неравенство) было верным:

5/10=*/2 ; 3/8>*/4 ; 1/2 3/5.

В) Сравнить дроби с разными числителями и знаменателями:

3/7 4/9 . Подвести к случаю А), найдя НОК, 3/7=27/63 4/9=28/63

т.к. 27/63 или = знаменателю.

4)Для нахождения общего знаменателя надо находить НОК или НОД?

8)Действие, при помощи которого находят дробь от числа

9)Для сокращения дроби нужно находить НОД или НОК?

Ответы:

По горизонтали: 1)Сокращение 2)Отношение 3)Несократимая 4)Двенадцать 5)Процент

По вертикали: 6)Неправильная 7)НОК 8)Умножение 9)НОД

Команды получают жетоны, а команда-победитель выбирает маршрут.

Горы Мозгодром.

1)Как переложив одну спичку, получить число, равное 1/3?

2)Каждая команда получает карточку с заданием: Поставьте знаки действий так, чтобы равенства были верны.

7/8*11/7=1; 3/7*4/7=3/4; 2*11/3=2/3; 0,3*5/6=1/4;

3)Разделите 7 арбузов на 12 человек, сделав как можно меньше разрезов.

4)Каждая команда получает карточку с заданием:

Не выполняя деления, сравните значения выражений:

а) 12,5:0,5 и 25:0,5 б)12,5:0,5 и 12,5:2,5

в) 12,5:0,5 и 12,5:0,05 г)125:0,5 и 12,5:5

За каждое задание команды получают жетоны и выбирают маршрут.

Лес Сказочный.

Каждая команда получает по две карточки с заданием

Задание 1 Выполните действия по порядку и расшифруйте фамилию известной детской писательницы:

1)22/3+35/6 5)6*11/15

2)5-23/8 6)6:31/3

3)4/27*9/16 7)13/7*119/30

4)2,4:4/15 8)11/3:16

Задание 2 Расположите дроби в порядке возрастания и вы узнаете имя одного из ее героев.

0,5 6/7 2,25 5/2 1/3 8/4 1

А Р О Н К С Л

Команды получает жетоны.

Дополнительный вопрос Какие еще произведения этой писательницы вы знаете?

За ответ на это вопрос команды также получают жетоны.

Поляна Театральная.

К этому конкурсу команды готовятся заранее. Они показывают сценки, сказки, инсценируют стихи, песни о дробях.

Жюри подводит итоги конкурса и раздает жетоны. Победителем игры объявляется команда, набравшая большее количество жетонов. Ей вручается диплом.

Приложение 6.

Факультативное занятие №1.

Тема: Расширение множества чисел. Введение дробей.

Цели:

Сформировать представления учащихся о возникновении дробей.

Воспитывать умение слушать другого и воспринимать материал.

Развивать любознательность, вызвать интерес к изучению обыкновенных дробей.

Содержание занятия:

I Орг. Момент.

На сегодняшнем занятии мы с вами поговорим ою обыкновенных дробях.

II. Беседа.

Из истории о дробях.

В жизни человеку приходилось не только считать предметы, но и измерять величины. Люди встретились с измерениями длин, площадей земельных участков, объемов, массы тел. При этом случалось, что единица измерения не укладывалась целое число раз в измеряемой величине. Например, измеряя длину участка шагами, человек встречался с таким явлением: в длине укладывалось десять шагов и оставался остаток меньше одного шага.

Появление дробей связано у многих народов с делением добычи на охоте. В связи с этой необходимой работой дюди стали употреблять выражения: половина, треть, два с половиной шага. Откуда можно было сделать вывод, что дробные числа возникли как результат измерения величин.

2.Запись дробей.

Народы прошли через многие варианты записи дробей, пока не пришли к современной записи.

В

2

1

3

начале в записи дробей не использовалась дробная черта, например число записывалось так .

Черта дроби появилась лишь только в 1202 году у итальянского математика Леонардо Пизанского. Он ввел слово дробь. Названия числитель и знаменатель ввел в 13 веке Максим Плануд – греческий монах, ученый, математик.

Современную систему записи дробей создали в Индии. Только там писали знаменатель сверху, а числитель снизу, и не писали дробной черты. А записывать дроби как сейчас стали арабы.

3.Деление чисел – один из источников возникновения дробей.

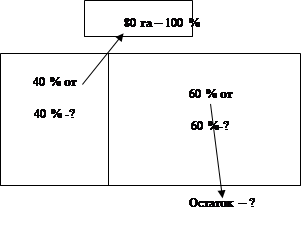
Древние ученые не считали числом результат деления дробных чисел. Например, 12/5=22/5 – дробный результат деления, но к числам его не относили. Интересные сведения об этом записаны в древних рукописях. Задача: «Разделить 100 фунтов между 11 людьми поровну».

Мы: 100/11=91/11

Древние математики 100/11 не считали дробью. Остаток от деления 1 фунт предлагается поменять на яйца, которых можно было купить 91 штуки. Если 91:11 то получится по 8 яиц и 3 яйца в остатке. Автор рекомендует отдать их тому, кто делил, или же поменять на соль, чтобы посолить яйца.

На этих примерах мы видим, что дроби входили в жизнь с большими трудностями.

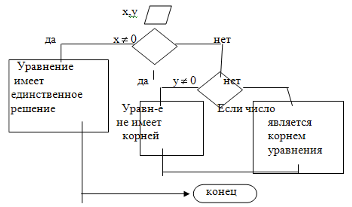
4.Решение уравнений.

Вначале уравнения, у которых в ответе получалось дробное число, считалось не имеющим решения, но постепенно в ответе стали записывать дробные числа. Например, решим уравнения:

А)3Х-(Х+18)=15 Б) (10Х-2Х):2=3

3Х-Х-18=15 8Х:2=3

2Х-18=15 8Х=6

2Х=33 Х=6/8=3/4

Х=161/2

В) 95-Х(32Х+18)+15=31

95Х-50Х+15=31

45Х+15=31

Х=16/45

Позднее дроби стали считать числами. Долгое время их называли ломаными числами. Как вы думаете, почему?

III. Итог занятия.

Какие три источника могли стать причиной возникновения дробей?

2. Как называются компоненты дроби?

3. Что означает черта дроби?

4. Какие дроби называют правильными?

Приложение 7 Факультативное занятие №2

Тема: Сравнение дробей

Ход занятия.

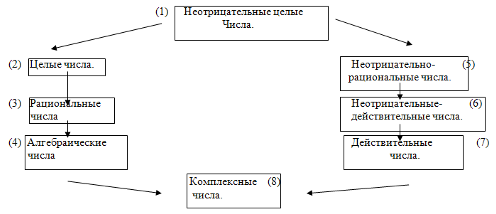
Вы получили некоторое представление о дробях, образующих новое, неизвестное вам множество чисел.

В множестве дробей также, как и в множестве натуральных чисел, производятся такие операции, как сравнение, сложение, вычитание, возведение в степень.

Мало того, известные вам натуральные числа стали представлять в виде дробей. Например, натуральное число 2 можно записать как 2/1=14/7=30/15 и т.д.

Не смотря на то, что натуральные числа можно рассматривать как частный случай дробных чисел. Действия с дробями совершенно не похожи на действия с натуральными числами.

Складывать и вычитать дробные числа, а также умножать и делить их нужно было по новым правилам, не похожим на правила действий с натуральными числами. Эти правила были разработаны древними математиками. Общим были лишь законы арифметических действий и некоторые определения. Например, умножение на натуральное число называлось сложением одинаковых слагаемых: 2/3*5=2/3+2/3+2/3+2/3+2/3=10/3=31/3

Введение дробей позволило выполнять деление натуральных чисел во всех случаях: 50/12=42/12, но это еще не облегчало выполнение других действий. Нелегко усваивались обыкновенные дроби. Они считались самым трудным разделом арифметики. Об этом можно судить по следующим фактам. У нас есть поговорка: «Попал в тупик», у немцев и ныне в ходу поговорка похожая на нашу: «Попал в дроби». Обе эти поговорки означают одно и тоже: человек попал в очень трудное положение.

Уже в древние времена математики разрабатывали правила действий с дробями, заставляя учащихся механически заучивать эти правила, не осознавая их смысла. Именно это было причиной тех. Порой непреодолимых затруднений, которые встречали учащиеся. В наше время из математики давно исчезли правила, которые дети не могли бы понять. Правила эти разъясняются на примерах, доказываются.

Поэтому вы видите, что обыкновенные дроби – интереснейший раздел математики.

3. Возьмем хотя бы операцию сравнения дроби. Какая из дробей больше: 2/5 или 3/5; 2/7 или 1/7 ?

Если вы разделите пирог на 5 равных частей и возьмете две такие части, то это меньше оставшихся 3/5 пирога.

А правило говорит: « Из двух дробей с одинаковыми знаменателями та меньше…». Но сравнивать иногда приходиться и такие дроби, как 3/8 и 5/12. Разрезание пирога здесь не поможет. Первая наша проблема научиться заменять дробь равной ей дробью, но с другим знаменателем.

4.Возьмем круг и разобьем его двумя 1/8

перпендикулярными диаметрами на 4 1/4

равные части. Каждая из них 1/4 круга.

Теперь каждую 1/4 разобьем на две

равные части, тогда круг разобьется

на ... равных частей, которых в 1/4 будет

две, т.е. 1/4=2/8.

Чтобы получить из 1/4 равную ей дробь 2/8, достаточно числитель и знаменатель дроби 1/4 ... .

Основное свойство дроби.

Если числитель и знаменатель дроби умножить или разделить на одно и тоже число не равное нулю, то получится дробь равная данной.

Вот теперь можно говорить о сравнении дробей 3/8 и 5/12.

Надо подыскать такое число, которое делилось бы как на 8, так и на 12. Таких чисел много. Самое меньшее из них – 24. На сколько надо умножить 8 и 12, чтобы получить 24? Получим дроби 9/24 и 10/24. Откуда заключаем, что 9/24 < 10/24, а значит 3/8 < 5/12.

Вывод: Для сравнения дробей удобно привести их к общему знаменателю, и считать ту дробь меньшей, у которой меньше числитель.

5. Задача: Найти две дроби, каждая из которых меньше 4/5 и больше 3/5.

Ясно, что эти дроби следует заменить равными им дробями, но с большими знаменателями. Умножим числитель и знаменатель на 2, получим 6/10 и 8/10. Дробь, больше 6/10 и меньше 8/10 может быть 7/10. Нам же требуется узнать две промежуточные дроби. Попробуем умножить числитель и знаменатель на 3. Имеем 3/5