Метод Ньютона-Рафсона, также известный как Метод Ньютона, представляет собой обобщенный метод поиска корня уравнения
|
| (1) |
Примем x = xj в качестве j-го приближения к корню уравнения (1). Предположим, что xj не является решением. Следовательно,
. Предположим также, что мы получили разложение в ряд Тейлора для уравнения (1) относительно точки x = xj:
|
| (2) |
Если примем в качестве следующего члена x = xj+1, то уравнение (2) будет иметь вид:
|
| (3) |
Теперь предположим, что справедливо необязательное допущение того, что предыдущее приближение xj было удовлетворительным, так что xj+1 - xj мало. Если это предположение верно, мы можем пренебречь членами более высокого порядка в уравнении (3), так как n-я степень малой величины значительно меньше, чем малая величина для n>=2. В этом случае уравнение (3) может быть аппроксимировано следующим образом:
|
| (4) |
Нашей целью является выбор такого xj+1, чтобы оно стало решением уравнения (1). Следовательно, если наше предыдущее предположение справедливо, xj+1 должно быть выбрано таким, что
. Приравняв уравнение (4) к нулю и решив относительно xj+1, получим:
|
| (5) |
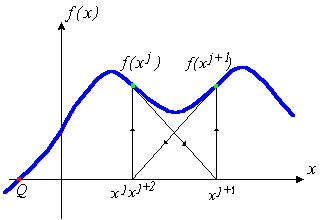
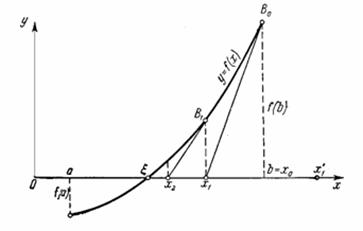
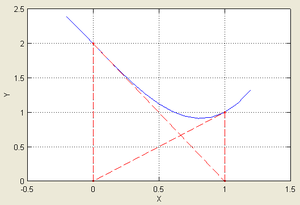
Уравнение (5) называется уравнением Ньютона - Рафсона. Если наше предположение, приведшее к выводу уравнения (5), справедливо, этот алгоритм будет сходящимся, но только в том случае, если точка начального приближения достаточно близка к точке решения. Геометрическая интерпретация сходящегося метода Ньютона - Рафсона приведена на рис. 1а.
|
|
|
| а) метод сходится | б) метод не сходится |
Рис.1. Геометрическая интерпретация метода Ньютона - Рафсона
Однако, если точка начального приближения далека от точки решения, то метод Ньютона - Рафсона может не сходиться совсем. Геометрическая интерпретация не сходящегося метода Ньютона - Рафсона приведена на рис. 1б.
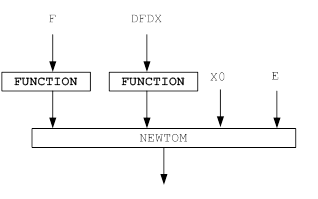
Алгоритм
Назначение: поиск решения уравнения (1)
Вход:
Начальное приближение x0
Точность (число итераций I)
Выход:
xI - решение уравнения (1)
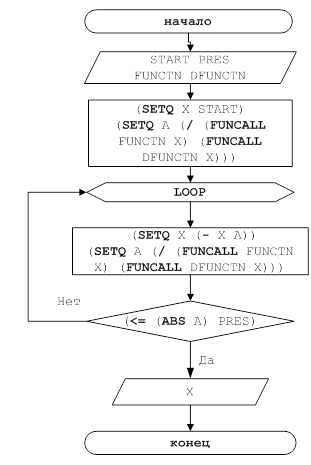
Инициализация:
calculate f’(x0)
Шаги:
1. repeat:
2. calculate xi using (5)
3. let i=i+1
4. if i>I then break the cycle
end of repeat
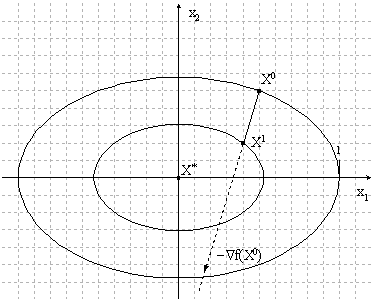
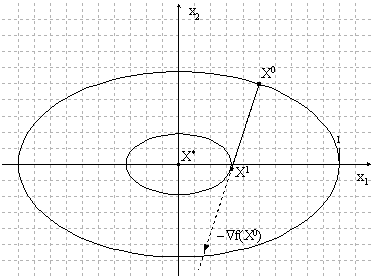
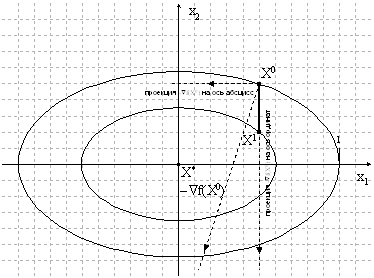
Модификация алгоритма Ньютона для решения системы нескольких уравнений заключается в линеаризации соответствующих функций многих переменных, т. е. аппроксимации их линейной зависимостью с помощью частных производных. Например, для нулевой итерации в случае системы двух уравнений:
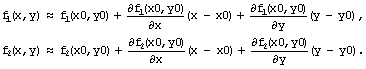
Чтобы отыскать точку, соответствующую каждой новой итерации, требуется приравнять оба равенства нулю, т.е. решить на каждом шаге полученную систему линейных уравнений.
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://www.xaoc.ru/
Похожие работы
... работы со справочной системой работа практикума приостанавливается. 3. Организационно-экономическое обоснование проекта В ходе дипломного проекта был разработан компьютерный лабораторный практикум по курсу «Теория оптимизации и численные методы». В данном разделе рассмотрена экономическая сторона проекта. Рассмотрены следующие вопросы: 1) сетевая модель 2) расчёт ...
... –0.6 = 0 9. 10. ( x -1)3 + 0.5ex = 0 11. 12. x5 –3x2 + 1 = 0 13. x3 –4x2 –10x –10 = 0 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. x 4- 2.9x3 +0.1x2 + 5.8x - 4.2=0 25. x4+2.83x3- 4.5x2-64x-20=0 26. МЕТОДЫ РЕШЕНИЯ СИСТЕМЫ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 1. Постановка задачи Пусть требуется решить систему n ...
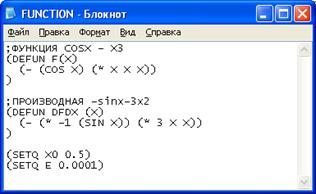
... метода Ньютона на случай мнимых корней полиномов степени выше второй и комплексных начальных приближений. Эта работа открыла путь к изучению теории фракталов. Целью данной курсовой работы является Лисп – реализация нахождения корней уравнения методом Ньютона. 1. Постановка задачи Дано уравнение: . Требуется решить это уравнение, точнее, найти один из его корней (предполагается, что ...
... при решении предусмотренных задач одна из эталонных схем (рабочая) копируется в рабочие файлы. Для моделирования, анализа и хранения режимов создана база режимов (до 12 режимов). Предусмотрена возможность записи произвольного режима, являющегося результатом решения одной из задач, в базу режимов. Все расчеты, включая и формирование отображаемых на дисплеях кадров, производятся на ЭВМ ИВП. В ИВП ...
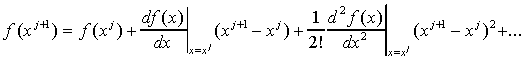
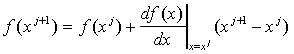
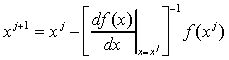
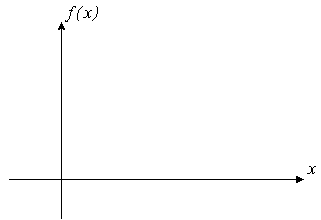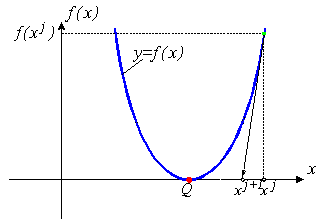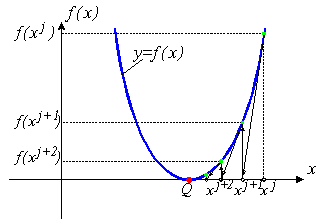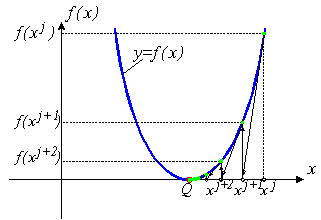
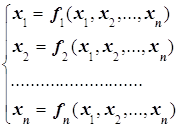
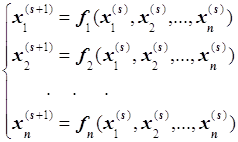
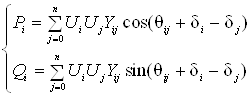
0 комментариев