Навигация
Расчет и анализ потерь активной мощности
Введение
Задачей дипломного проекта являлось изучение оценки состояния ЭЭС и концепций построения математического обеспечения информационно-вычислительных подсистем, знакомство с КП Компоновщик расчетных схем, освоение Windows‑программирования, приобретение навыков работы в интегрированной среде Developer Studio и разработка некоторых элементов пользовательского интерфейса Компоновщика расчетных схем в операционной системе Windows.
В первой главе была выбрана математическая модель режима, рассмотрены несколько критериев оценки состояния ЭЭС. Обоснован выбор метода обобщенной нормальной оценки для оценивания состояния ЭЭС, как обладающего существенными преимуществами по сравнению с другими критериями. В качестве численного метода принят в общем случае метод Ньютона-Рафсона. Наряду с этим методом, при наличии некоторых условий целесообразно применять метод Ньютона-Рафсона по параметру. Для решения систем линейных уравнений по итерационным формулам используется метод Гаусса (LU‑разложение). Вычисления производятся с учетом свойств разреженных матриц. Показано разнесение вычислений вне реального времени (на подготовительном этапе) и непосредственно в реальном времени.
Во второй главе рассматривается назначение и функциональные возможности программы Компоновщик расчетных схем. Приведен алгоритм формирования расчетной схемы, удовлетворяющий требованиям, предъявляемым к системам подготовки, отладки и поддержания данных.
В третьей главе описываются основные особенности Windows‑программирования: процесс создания главного окна программы, процедуры обработки сообщений. Показываются отличия модальных и немодальных окон диалога. Приводится описание панелей инструментов и состояния. Подробно показан процесс создания и работы строкового и оконного редакторов, реализация функций, предоставляемых пользователю.
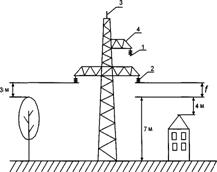
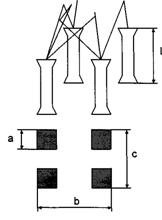
В последней, четвертой, главе рассматривается вопрос из раздела техники безопасности на тему: «Разработка мероприятий по безопасной эксплуатации ПЭВМ».
1. Оценка состояния
1.1 Постановка задачи
Инвариантность поведения автоматизированной системы диспетчерского управления (АСДУ) относительно внешних возмущений, а, значит, обоснованность принятых решений и эффективность управлением режимом энергосистемы в реальном времени может быть обеспечена в принципе, если используется достоверная информация о параметрах режима и схеме электрических соединений, о составе и состоянии основного оборудования, о параметрах и характеристиках отдельных объектов, и т.д. Наиболее важным и трудным оказывается получение информации о текущих параметрах режима и схеме электрических соединений, требующей проведения измерений в реальном времени. Непосредственное измерение всех параметров режима невозможно, недостающая часть должна быть восстановлена расчетным путем. Низкая достоверность телеизмеряемой информации, возможные отказы каналов связи, ограниченные возможности информационно-измерительной сети затрудняют непосредственное воспроизведение физики явлений. Повысить достоверность телеизмерений (ТИ), восстановить расчетным путем недостающую часть параметров режима, воспроизвести физику явлений позволяют методы теории оценок, которые делятся на две группы: методы, учитывающие априорную информацию об оцениваемых параметрах режима; методы, не учитывающие такую информацию.
Установившийся режим электроэнергетической системы (ЭЭС) описывается системой нелинейных алгебраических уравнений
![]() (1.1)
(1.1)
где x, у – соответственно оцениваемые и измеряемые параметры режима.
Форма записи (1.1) зависит от выбранной схемы замещения отдельных элементов и системы координат, разделения параметров режима на измеряемые и оцениваемые; конкретный состав системы – составом используемых ТИ. Разделение параметров режима на оцениваемые и измеряемые производится по смыслу решаемой задачи; руководствоваться следует лишь двумя требованиями: в качестве оцениваемых принимаются те, зная которые, легко рассчитать все остальные параметры режима без решения дополнительной системы уравнений; в конечном счете необходимо получить параметры режима, которые будут использованы в дальнейшем при оптимизации. По техническим соображениям, а также для потребностей диспетчерского персонала, измеряются потоки мощностей по ветвям и узлах, напряжения, токи в ветвях. Это и определяет выбор оцениваемых параметров режима – модули и фазы или действительные и мнимые части узловых напряжений.
Связь между оцениваемыми и измеряемыми параметрами режима
y = f(x) (1.2)
устанавливается уравнениями потокораспределения, конкретный вид которых определяется выбранной формой записи, в частности:
à для суммарной активной и реактивной мощности в i-ом узле
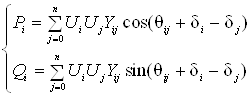 (1.3)
(1.3)
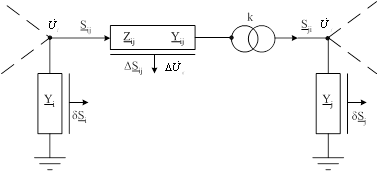
à для потоков мощностей в начале ветви (i, j)
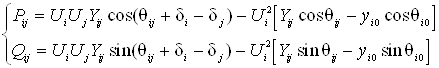 (1.4)
(1.4)
где: n – число независимых узлов; ![]() – узловые напряжения (
– узловые напряжения (![]() );
);![]()
![]() – проводимость ветви (i, j) (
– проводимость ветви (i, j) (![]() );
); ![]() – проводимость на землю в узле i (
– проводимость на землю в узле i (![]() ).
).
После введения матричных обозначений:
![]() ,
, ![]()
мы и получаем (1.2).
В измерениях, проводимых в реальной ЭЭС, всегда присутствуют погрешности, обусловленные погрешностями измерительной аппаратуры, помехами в каналах связи, неодновременностью замеров, поэтому вектор измерений ![]() может быть представлен суммой вектора истинных значений у и вектора ошибок w
может быть представлен суммой вектора истинных значений у и вектора ошибок w
![]() у + w (1.5)
у + w (1.5)
Если предположить, что случайный вектор ошибок распределен по нормальному закону
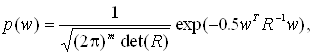 (1.6)
(1.6)
где R – ковариационная матрица ошибок измерений; m – число измерений, то наиболее правдоподобными считаются те значения w, при которых достигается максимум плотности распределения (используется метод максимального правдоподобия, основанный на максимизации функции (1.6), называемой функцией правдоподобия. Эта показательная функция достигает своего максимума, когда ее показатель минимален [1]).
В общем случае в качестве меры близости измеренных параметров режима ![]() и их расчетных значений f(x) может быть выбран критерий
и их расчетных значений f(x) может быть выбран критерий
![]() (1.7)
(1.7)
Задача оценки состояния ЭЭС сводится к нахождению такого вектора оцениваемых параметров режима, который доставляет значения измеряемым, близкие к измеренным в смысле выбранного критерия (1.7)
Оценка состояния ЭЭС – сложный процесс, в котором можно выделить ряд основных этапов:
1. Выбор математической модели режима.
2. Построение критерия оценки.
3. Разработка численного метода и алгоритма оценивания.
Деление носит условный характер, все этапы взаимосвязаны: свойства математической модели режима являются определяющими при построении критерия оценивания, алгоритм оценивания должен учитывать как свойства выбранного критерия близости, так и математической модели режима. В конечном счете, алгоритм оценивания должен удовлетворять следующим требованиям: высокая скорость и надежность сходимости, высокая точность и устойчивость результатов, высокое быстродействие, незначительный объем требуемой оперативной памяти ЭВМ.
Рассмотрим подробнее каждый из этапов.
1.2 Математическая модель режима
Если в начале каждой ветви дерева измеряется поток активной и реактивной мощности, то соответствующая математическая модель режима имеет единственное решение в целом. Любая модель режима, полученная из указанной добавлением новых измеряемых параметров режима, также имеет единственное решение [1].
Модель режима называется корректной, если [1]:
1. для любого y существует решение (условие разрешимости);
2. решение является единственным (условие однозначности);
3. решение непрерывно зависит от у (условие устойчивости).
При нарушении хотя бы одного из этих условий задача оценки состояния называется некорректно поставленной (математическая модель называется некорректно поставленной).
1.3 Критерий оценки
На выбор критерия оценки влияют: характер исследуемого процесса (статический или динамический), наличие или отсутствие статистических данных об измеряемых и оцениваемых параметрах, корректная или некорректная постановка задачи. Определяющей является некорректная постановка задачи оценивания состояния ЭЭС. Она проявляется в том, что сколь угодно малые погрешности измерений приводят к сколь угодно большим ошибкам в результатах оценки. Метод максимального правдоподобия дает один из наиболее распространенных критериев.
![]() (1.8)
(1.8)
причем оценка состояния ЭС сводится к нахождению
![]() (1.9)
(1.9)
Метод, основанный на (1.9) (метод взвешенных наименьших квадратов), позволяет получить такую оценку, которая доставляет значения измеряемым параметрам режима, близкие к измеренным в смысле минимума дисперсии измерений.
Если матрица ковариации ошибок измерений R неизвестна или ее получение затруднено, вместо (1.8) используется
![]() (1.10)
(1.10)
и оценка находится из условия достижения
![]() (1.11)
(1.11)
Метод, основанный на (1.11) (метод наименьших квадратов), позволяет получить такую оценку ![]() , которая доставляет значения измеряемым параметрам режима, близкие к измеренным в смысле минимума суммы квадратов невязок.
, которая доставляет значения измеряемым параметрам режима, близкие к измеренным в смысле минимума суммы квадратов невязок.
Если система нелинейных алгебраических уравнений совместна, то решения (1.9.) и (1.11) совпадают. Для переопределенных и несовместных нелинейных алгебраических уравнений решение (1.9) и (1.11), вообще говоря, не совпадают: решение (1.9) зависит от выбора матрицы ковариаций.
Некорректность математической модели режима отражается на свойствах этих критериев, характере решения задачи оценивания:
1. нарушено требование однозначности – критерий оценки является многоэкстремальной функцией; каждое решение модели режима – это точка экстремума критерия оценки;
2. нарушено требование разрешимости – выполняется необходимое условие существования минимума, ранг матрицы частных производных ![]() понижается;
понижается;
3. нарушено требование непрерывности либо критерий оценки не имеет минимума в области определения (в целом), либо выполняется необходимое условие существования минимума, ранг матрицы частных производных ![]() понижается.
понижается.
Использование рассмотренных методов с учетом некорректности постановки задачи оценивания состояния ЭЭС становится проблематичным.
Наличие априорных данных ![]() об оцениваемых параметрах и матрице ковариации ошибок задания априорных данных S позволяет использовать критерий
об оцениваемых параметрах и матрице ковариации ошибок задания априорных данных S позволяет использовать критерий
![]() (1.12)
(1.12)
и получить оценку из условия достижения
![]() (1.13)
(1.13)
Метод, реализующий (1.13) (байесова оценка), в ряде случаев позволяет локализовать нужное решение за счет использования априорных данных.
Каждый из рассмотренных методов имеет свои недостатки и достоинства. Общим недостатком является невозможность использования для оценки состояния ЭЭС с учетом ее некорректной постановки.
Для решения некорректно поставленных задач был предложен метод регуляризации
![]()
![]() a>0,
a>0,
где ![]() – сглаживающая или регуляризующая функция;
– сглаживающая или регуляризующая функция; ![]() – стабилизирующая функция;
– стабилизирующая функция; ![]() – параметр регуляризации.
– параметр регуляризации.
Идея метода основана на использовании априорных сведений об оцениваемых параметрах: физический смысл имеют только ограниченные решения.
Проведенные исследования [1] показали:
1) если решение математической модели режима является неоднозначным, то локализовать нужное (действительное) не всегда удается;
2) возможны случаи, когда итерационный процесс решения (1.8) затягивается – в стабилизирующую функцию входят несоизмеримые по величине параметры режима, и стремление ограничить решение приводит к чрезмерному сглаживанию;
3) целесообразность задания априори параметра регуляризации.
Недостатки метода регуляризации могут быть устранены после соответствующей его модификации.
Похожие работы
... (от передвижения источников загрязнения) 1180,48 Всего за год: 211845,25 10. Совершенствование системы электроснабжения подземных потребителей шахты Расчет схемы электроснабжения ЦПП до участка и выбор фазокомпенсирующих устройств Основными задачами эксплуатации современных систем электроснабжения горных предприятий являются правильное определение электриче ...
... luc – программа используется для разложения матрицы на треугольные сомножители; rluc – программа, которая отвечает за решение системы уравнений. 4. Разработка адаптивной системы управления режимами электропотребления 4.1 Функции автоматизированной системы Сбор, накопление и передача информации, характеризующей режим электропотребления комбината (информация о нагрузках). Сбор, накопление ...
... Еловка ТМН-2500/35 ±6×1,5% Ужурсовхоз ТМН-4000/35 ±6×1,5% 2. Характеристика задачи расчета, анализа и оптимизации режимов РЭС 110-35 кВ по напряжению, реактивной мощности и коэффициентам трансформации Питающие электрические сети напряжением 110 кВ, ...
... линиям относят линии, для которых верхняя граница интервала неопределенности потерь превышает установленную норму (например, 5%). 3. Программы расчета потерь электроэнергии в распределительных электрических сетях 3.1 Необходимость расчета технических потерь электроэнергии В настоящее время во многих энергосистемах России потери в сетях растут даже при уменьшении энергопотребления. При ...
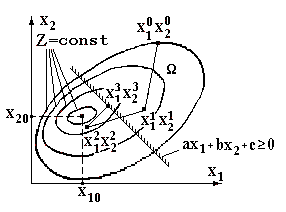
0 комментариев