Расширение библиотеки функций dlisp

3. Расширение библиотеки функций dlisp.

Основные принципы программирования на dlisp те же, что и в MuLisp, при этом сохраняется и синтаксис MuLispа.

Никогда не используйте имена встроенных функций или символов для функций, определяемых вами, так как это сделает недоступными встроенные функции.

Пример расширения библиотеки функций dlispа содержится в файле rash.lsp. Для его запуска необходимо выполнить следующую последовательность команд:

MuLisp87.com Common.lsp

(load rash.lsp)

;File rash.lsp

;(Приложение к учебной версии языка Лисп dlisp).

;Содержит функции, расширяющие библиотеку dlisp Лиспа.

;Функция APPEND1 соединяет два списка в один

(defun append1 (l p)

(if (null l) p ;L пуст - вернуть P (условие окончания),

(cons (car l) ;иначе - создать список,

(append1 (cdr l) p)))) ;используя рекурсию.

;EQUAL1 - логическая идентичность объектов (параллельная рекурсия)

(defun equal1 (u v)

(cond ((null u) (null v)) ;возвращает T если U и V пустые

((numberp u) (if (numberp v) (= u v) ; проверка

nil)) ;на идентичность

((numberp v) nil) ; чисел

((atom u) (if (atom v) (eq u v) ;сравнение атомов

nil))

((atom v) nil)

(t (and (equal1 (car u) (car v)) ; идентичность "голов"

(equal1 (cdr u) (cdr v)))))) ;идентичность "хвостов"

;DELETE1 - удаляет элемент X из списка L

(defun delete1 (x l)

(cond ((null l) nil)

((equal1 (car l) x) (delete1 x (cdr l)))

(t (cons (car l) (delete1 x (cdr l)))))) ;ветвь выполняется

;в случае невыполнения предыдущих.

;FULLENGTH1 - определяет полную длину списка L (на всех уровнях)

(defun fullength1 (l)

(cond ((null l) 0) ;для пустого списка возвращается 0

((atom l) 1) ;если L является атомом - возвращается 1

(t (+ (fullength1 (car l)) ;подсчет в глубину

(fullength1 (cdr l)))))) ;подсчет в ширину

;DELETELIST1 - удаляет все элементы, входящие в список U из списка V

(defun deletelist1 (u v)

(cond ((null u) v)

(t (delete1 (car u)

(deletelist1 (cdr u) v)))))

;MEMBER1 - проверяет вхождение элемента U в список V на верхнем уровне

(defun member1 (u v)

(cond ((null v) nil)

((equal1 u (car v)) v)

(t (member1 u (cdr v)))))

;В случае присутствия S-выражения U в списке V функция возвращает остаток списка V, начинающийся с U, в противном случае результатом вычисления является NIL.

;INTERSECTION1 - вычисляет список общих элементов двух списков

(defun intersection1 (u v)

(cond ((null u) nil)

((member1 (car u) v);проверка на вхождение "головы" сп. U в сп. V

(cons (car u) (intersection1 (cdr u) v)));создание списка

(t (intersection1 (cdr u) v))));ненужные элементы отбрасываются

;UNION1 - объединяет два списка, но в отличие от APPEND1,

;в результирующий список не добавляются повторяющиеся элементы

(defun union1 (u v)

(cond ((null u) v)

((member1 (car u) v) ;отсеивание

(union1 (cdr u) v)) ; ненужных элементов

(t (cons (car u)

(union1 (cdr u) v)))))

;COPY-LIST1 - копирует верхний уровень списка

(defun copy-list1 (l)

(cond ((null l) nil)

(t (cons (car l)

(copy-list1 (cdr l))))))

;COPY_TREE1 - копирует списочную структуру

(defun copy-tree1 (l)

(cond ((null l) nil)

((atom l) l)

(t (cons (copy-tree1 (car l))

(copy-tree1 (cdr l))))))

;ADJOIN1 - добавляет элемент к списку

(defun adjoin1 (x l)

(cond ((null l) nil)

((atom l) (cons x ;если L атом, то он преобразуется в список,

(cons l nil))) ;а затем к нему добавляется X

(t (cons x l))))

;SET-DIFFERENCE1 - находит разность двух списков

(defun set-difference1 (w e)

(cond ((null w) nil)

((member1 (car w) e) ;отбрасываются ненужные

(set-difference1 (cdr w) e)) ;элементы

(t (cons (car w)

(set-difference1 (cdr w) e)))))

;COMPARE1 - сравнение с образцом

(defun compare1 (p d)

(cond ((and (null p) (null d)) t) ;исчерпались списки?

((or (null p) (null d)) nil) ;одинакова длина списков?

((or (equal1 (car p) '&) ;присутствует в образце атом &

(equal1 (car p) (car d))) ;или головы списков равны

(compare1 (cdr p) (cdr d))) ;& сопоставим с любым атомом

((equal1 (car p) '*) ;присутствует в образце атом *

(cond ((compare1 (cdr p) d)) ;* ни с чем не сопоставима

((compare1 (cdr p) (cdr d))) ;* сопоставима с одним атомом

((compare1 p (cdr d))))))) ;* сопоставима с несколькими

;атомами

;SUBSTITUTE1 - замена в списке L атома S на атом N

(defun substitute1 (n s l)

(cond ((null l) nil)

((atom (car l))

(cond ((equal1 s (car l))

(cons n (substitute1 n s (cdr l))))

(t (cons (car l) (substitute1 n s (cdr l))))))

(t (cons (substitute1 n s (car l))

(substitute1 n s (cdr l))))))

;DELETE-DUPLICATES1 - удаление повторяющихся элементов

(defun delete-duplicates1 (l)

(cond ((null l) nil)

((member1 (car l) (cdr l))

(delete-duplicates1 (cdr l)))

(t (cons (car l) (delete-duplicates1 (cdr l))))))

;ATOMLIST1 - проверка на одноуровневый список

(defun atomlist1 (l)

(cond ((null l) t)

((listp (car l)) nil)

(t (atomlist1 (cdr l)))))

;REVERSE1 - обращает верхний уровень списка

(DEFUN REVERSE1 (l)

(COND ((NULL l ) NIL)

(T (APPEND1 (REVERSE1 (CDR l))

(CONS (CAR l) NIL)))))

4. Задание к лабораторной работе.

Напишите функцию, аналог системной функции Лиспа:

1. а) (1+ ) Результат функции - , увеличенное на единицу.

в) (1- ) Результат функции - , уменьшенное на единицу.

2. а) (incf память приращение) Добавление приращения к числу в памяти.

в) (decf память приращение) Вычитание приращения из числа в памяти.

3. (expt ) Эта функция возвращает , возведенное в указанную . Если оба аргумента целые, то результат - целое число. В любом другом случае, результат - действительное число.

4. (gcd ) Функция возвращает наибольший общий делитель и . и должны быть целыми.

5. а) (first ), second, third, и т. д. возвращающие соответственно первый, второй, третий, и т. д. элемент списка.

в) (last ) Эта функция возвращает последний элемент списка. не должен быть равен nil. LAST возвращает либо атом либо список.

6. а) (max ...) Эта функция возвращает наибольшее из заданных чисел.

в) (min ...) Эта функция возвращает наименьшее из заданных чисел.

7. а) (evenp ) Проверяет, четное ли число. Она возвращает T - если число четное и NIL - в противном случае.

в) (oddrp ) Эта функция - противоположная по действию функции evenp.

8. которая сортирует числа:

а) по возрастанию.

в) по убыванию.

9. предикат - который определяет:

а) числа с плавающей запятой.

в) целые числа.

г) строковые константы.

д) символы.

е) списки.

10. зависящую от одного аргумента, которая генерирует все циклические перестановки списка.

11. зависящую от одного элемента, которая по данному списку вычисляет список его элементов:

а) встречающихся в нем более 1, 2, ... раз.

в) встречающихся в нем не менее 2, 3, ... раз.

S. Запишите все функции, написанные вами, в один файл. Для отладки программы используйте встроенные средства dlispа.

5. Вопросы.

1. Какие способы тестирования программ предусмотрены в dlisp?

2. В чем их различия?

3. Какие функции предусмотрены для работы со строковыми константами в dlisp?

4. Назовите их основные особенности?

Список использованной литературы.

Э. Чювенен, И. Сеппянен

«Мир Лиспа»

Москва «Мир» 1990 г. Т.1

2. Э. Чювенен, И. Сеппянен

«Мир Лиспа»

Москва «Мир» 1990 г. Т.2

«Программирование на языке R-Lisp»

Москва «Радио и связь» 1991 г.

У. Маурер

«Введение в программирование на языке Лисп»

Москва «Мир» 1976 г.

Похожие работы

Лисп-реализация конечных автоматов

Скачать

14593

2

12

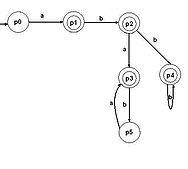
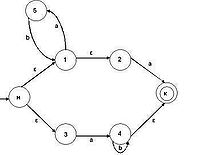
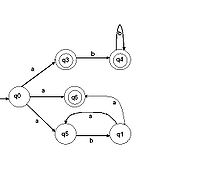
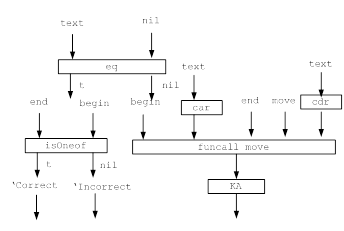
... цифр с требуемым числом разрядов и, таким образом, запомнить любое самое большое число данной разрядности. Целью данной курсовой работы является ЛИСП-реализация конечных автоматов.1. Постановка задачи Конечный автомат – автомат, проверяющий допустимость слова на ленте, и возвращающий True / False (в данном случае Correct / Incorrect). Конечный автомат может двигаться по ленте только в одном ...

ЛИСП-реализация основных операций над базами данных

Скачать

16057

6

13

... При работе пользователя с базой данных над ее содержимым выполняются следующие основные операции: выбор, добавление, модификация (замена) и удаление данных. Целью данной курсовой работы является ЛИСП – реализация основных операций над базами данных. 1 Постановка задачи Требуется разработать программу, реализующую основные операции над базами данных: выбор, добавление, модификация и удаление ...

ЛИСП-реализация основных операций над нечеткими множествами

Скачать

14282

0

14

... новых рынков, биржевой игре, оценки политических рейтингов, выборе оптимальной ценовой стратегии и т.п. Появились и коммерческие системы массового применения. Целью данной курсовой работы является ЛИСП – реализация основных операций над нечеткими множествами. 1.Постановка задачи Требуется реализовать основные операции над нечеткими множествами: 1)   содержание; 2)   равенство; 3)   ...

Нахождение корней уравнения методом Ньютона (ЛИСП-реализация)

Скачать

11806

0

10

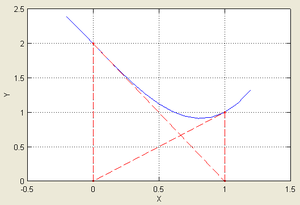
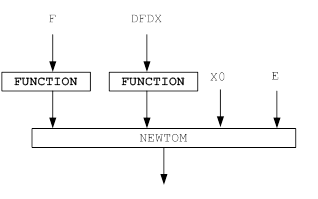
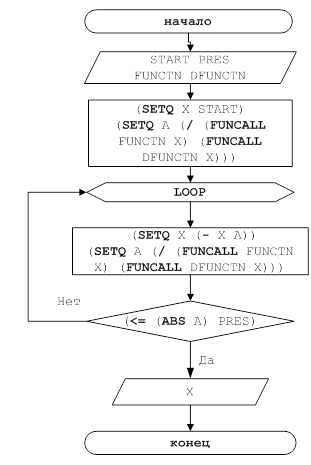
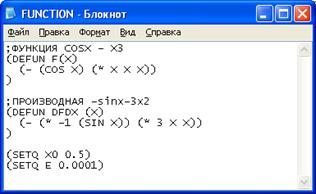
... метода Ньютона на случай мнимых корней полиномов степени выше второй и комплексных начальных приближений. Эта работа открыла путь к изучению теории фракталов. Целью данной курсовой работы является Лисп – реализация нахождения корней уравнения методом Ньютона. 1. Постановка задачи Дано уравнение: . Требуется решить это уравнение, точнее, найти один из его корней (предполагается, что ...