Навигация
5643 Ключевое слово
———————————————————————————————————————————————————————————————————————
|———————————————————————————————————————————————————————————————————————|
|———————————————————————————————————————————————————————————————————————|
|———————————————————————————————————————————————————————————————————————|
|———————————————————————————————————————————————————————————————————————|
|———————————————————————————————————————————————————————————————————————|
|———————————————————————————————————————————————————————————————————————|
———————————————————————————————————————————————————————————————————————
![]()
![]()
![]()
Введение
Проникновение математики в экономическую науку связано с преодолением значительных трудностей. В этом отчасти была “повинна” математика, развивающаяся на протяжении нескольких веков в основном в связи с потребностями физики и техники. Ног главные причины лежат все же в природе экономических процессов, в специфики экономической науки.
Большинство объектов, изучаемых экономической наукой, может быть охарактеризовано кибернетическим понятием сложная система.
Наиболее распространено понимание системы как совокупность элементов, находящихся во взаимодействии и образующих некоторую целостность, единство. Важным качеством любой системы является эмерджентность – наличие таких свойств, которые не присущи ни одному из элементов, входящих в систему. Поэтому при изучении систем недостаточно пользоваться методом их расчленения на элементы с последующим изучением этих элементов в отдельности. Одна из трудностей экономических исследований – в том, что почти не существует экономических объектов, которые можно было бы рассматривать как отдельные (внесистемные) элементы.
Сложность системы определяется количеством входящих в нее элементов, связями между этими элементами, а также взаимоотношениями между системой и средой. Экономика страны обладает всеми признаками очень сложной системы. Она объединяет огромное число элементов, отличается многообразием внутренних связей с другими системами (природная среда, экономика других стран и т. д.). В народном хозяйстве взаимодействуют природные, технологические, социальные процессы, объективные и субъективные факторы.
Сложность экономики иногда рассматривалась как обоснование невозможности ее моделирования, изучение средствами математики. Но такая точка зрения в принципе неверна. Моделировать можно объект любой природы и любой сложности. И как раз сложные объекты представляют собой наибольший интерес для моделирования; именно здесь моделирование может дать результаты, которые нельзя получить другими способами исследования.
Потенциальная возможность математического моделирования любых экономических объектов и процессов не означает, разумеется, ее успешной осуществимости при данном уровне экономических и математических знаний, имеющийся конкретной информации и вычислительной технике. И хотя нельзя указать абсолютные границы математической формализуемости экономических проблем, всегда будут существовать еще неформализованные проблемы, а также ситуации, где математическое моделирование недостаточно эффективно.
1. Краткое описание модели поставленной задачи
Благодаря своему широкому применению, теория о нахождении кратчайших путей в последнее время интенсивно развивается.
Нахождение кратчайшего пути - жизненно необходимо и используется практически везде, начиная от нахождения оптимального маршрута между двумя объектами на местности (напр. кратчайший путь от дома до академии),также используется в системах автопилота, используется для нахождения оптимального маршрута при перевозках коммутации информационного пакета Internet и мн. др.
Кратчайший путь рассматривается при помощи некоторого математического объекта, называемого графом. Граф задается множеством точек (вершин) и множеством линий (ребер), соединяющих все или часть этих точек.
Сетевые модели используются для решения следующих задач:
проектирование газопровода;
нахождение кратчайшего маршрута между городами по сети дорог;
определение максимальной пропускной способности при транспортировки нефти;
составление временных графиков работ и др.
Существуют три наиболее эффективных алгоритма нахождения кратчайшего пути:
1) алгоритм построения минимального основного дерева. Предполагает соединение всех узлов сети с помощью путей наименьшей длины.
2) алгоритм Дейкстры. Используется для нахождения кратчайшего пути между заданным исходным узлом и любым другим узлом сети
3) алгоритм Флойда. Используется для нахождения оптимального маршрута между любыми двумя узлами сети.
Основные определения
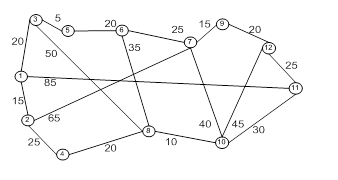
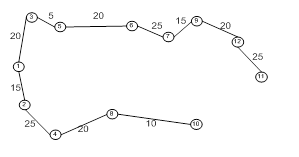
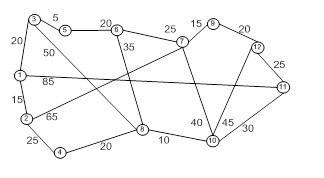
Сеть состоит из множества улов, связанных дугами (или ребрами). Таким образом, сеть описывается парой множеств (N,A), где N – множество узлов, а A – множество ребер. Например, сеть, показанная на рис. 1, описывается след образом.
N = {1, 2, 3, 4, 5},
A = {(1, 3), (1, 2), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5)}.
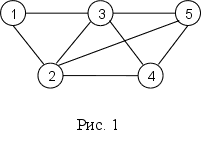
С каждым типом сети связан определенный тип потоков (например, транспортный поток нефти в нефтепроводах или автомобильные потоки в сети дорог). В общем случае потоки в сети ограничены пропускной способностью ее ребер, которая может быть как конечной, так и бесконечной.
Ребро называется направленным, или ориентированным (и в этом случае ребро будем называть дугой), если в одном направлении возможен только положительный поток, а в противоположном – только нулевой. В ориентированной сети все ребра ориентированы.
Путем называется последовательность различных ребер, соединяющих два узла, независимо от направления от направления потока в каждом ребре. Путь формирует цикл, если начальный и конечный узлы совпадают. Например, на рис. 2 ребра (2, 3), (3, 4) и (4, 2) составляют цикл. Ориентированный цикл – это цикл, в котором все дуги ориентированы в определенном направлении.
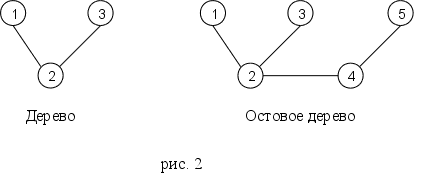
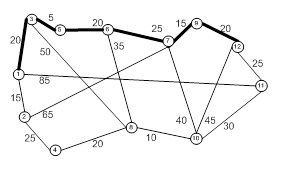
Связная сеть – такая сеть, у которой любые два узла связаны по крайней мере одним путем. На рис. 1 показан именно такой тип сети и не имеющий циклов. Остовное дерево – это дерево, содержащая все узлы сети. На рис. 2 показаны дерево и Остовное дерево для сети из рис. 1.
Похожие работы
... данных будет нести больше смысла, если его отсортировать каким‑либо образом. Часто требуется сортировать данные несколькими различными способами. Во‑вторых, многие алгоритмы сортировки являются интересными примерами программирования. Они демонстрируют важные методы, такие как частичное упорядочение, рекурсия, слияние списков и хранение двоичных деревьев в массиве. Наконец, сортировка ...
... сети телекоммуникаций, а также сравнивая технические возможности оборудований различных фирм в настоящем дипломном проекте предлагаю создать интеллектуальную сеть в г.Кокшетау на базе оборудования S-12 фирмы Alcatel [6]. Выбор оборудования не случаен, так как на сети города полностью эксплуатируется данная система. Это позволяет оптимально решить вопросы по синхронизации, сигнализации и по ...
элементы теории нечетких множеств можно применять для решения экономических задач в условиях неопределённости. 1. применение Логических функций 1.1 Применение методов дискретной математики в экономике При исследовании, анализе и решении управленческих проблем, моделировании объектов исследования и анализа широко используются методы формализированного представления, являющегося предметом ...
... реализуется тем лучше, чем четче будет организовано выполнение всех работ по подготовке и обеспечению перевозочного процесса. Однако организация автомобильных перевозок грузов из одной страны в другую - процесс сложный, требующий соблюдения международных конвенций и соглашений по перевозкам и транзиту, высокого качества обслуживания, точного исполнения условий контракта, соблюдения таможенных и ...


0 комментариев