Навигация
Математическая формулировка задачи, обоснование
2. Математическая формулировка задачи, обоснование
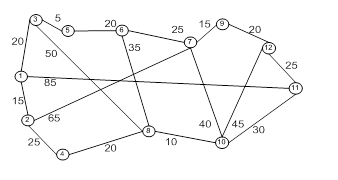
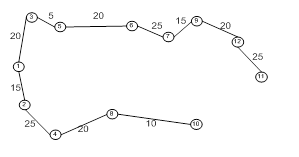
Алгоритм ФлойдаАлгоритм Флойда находит кратчайший путь между любыми двумя узлами сети. В этом алгоритме сеть представлена в виде квадратной матрицы с n строками и n столбцами. Элемент (i ,j) равен расстоянию dij от узла i к узлу j, которое имеет конечное значение, если существует дуга (i ,j), и равен бесконечности в противном случае.
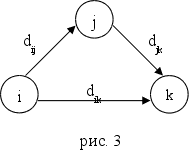
Покажем сначала основную идею метода Флойда. Пусть есть три узла i, j и k и заданы расстояния между ними (рис. 3). Если выполняется неравенство dij+ djk < dik, то целесообразно заменить путь i → k путем i → j → k. Такая замена (далее ее будем условно называть треугольным оператором) выполняется систематически в процессе выполнения алгоритма Флойда.
Алгоритм Флойда требует выполнения следующих действий.
Шаг 0. Определяем начальную матрицу расстояний D0 и матрицу последовательности
узлов S0. Диагональные элементы обеих матриц помечаются знаком “ – “,
показывающим, что эти элементы в вычислениях не участвуют. Полагаем k=1.
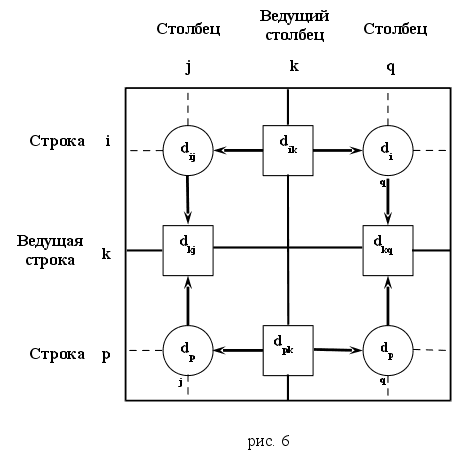
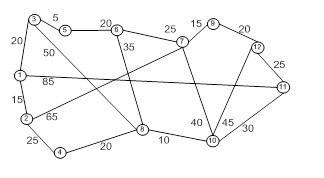
Основной шаг. Задаем строку k и столбец k как ведущую строку и ведущий столбец.
Рассматриваем возможность применения треугольного оператора ко всем элементам dijматрицы Dk-1. Если выполняется неравенство
dij+ djk < dik (i ≠k, j≠k, i ≠j),
тогда выполняем следующие действия :
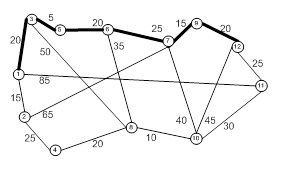
создаем матрицу Dk путем замены в матрице Dk-1 элемента dij на сумму dij+ djk, (рис. 4)
создаем матрицу Sk путем замены в матрице Sk-1 элемента sij на k. Полагаем k=k+1 и повторяют шаг k. (рис. 5)
| – | d12 | … | d1j | … | d1n |
| d21 | – | … | d2i | … | d2n |
| . . . | . . . | . . . | . . . | . . . | . . . |
| di1 | di2 | … | dij | … | din |
| . . . | . . . | . . . | . . . | . . . | . . . |
| dn1 | dn2 | … | dnj | … | – |

рис. 4

| – | 2 | … | j | … | n |
| 1 | – | … | j | … | n |
| . . . | . . . | . . . | . . . | . . . | . . . |
| 1 | 2 | … | j | … | n |
| . . . | . . . | . . . | . . . | . . . | . . . |
| 1 | 2 | … | j | … | – |
рис. 5
После реализации n шагов алгоритма определение по матрицам Dnи Snкратчайшего пути между узлами i и j выполняется по следующим правилам .
Расстояние между узлами i и j равно элементу dij в матрице Dn.
Промежуточные узлы пути от узла i до узла j определяем по матрице Sn. Пусть sij = k, тогда имеем путь i → j → k. Если далее sik = k и ski = j, тогда считаем, что весь путь определен, так как найдены все промежуточные узлы. В противном случае повторяем описанную процедуру для путей от узла i к узлу k и от узла k к узлу j.

Похожие работы
... данных будет нести больше смысла, если его отсортировать каким‑либо образом. Часто требуется сортировать данные несколькими различными способами. Во‑вторых, многие алгоритмы сортировки являются интересными примерами программирования. Они демонстрируют важные методы, такие как частичное упорядочение, рекурсия, слияние списков и хранение двоичных деревьев в массиве. Наконец, сортировка ...
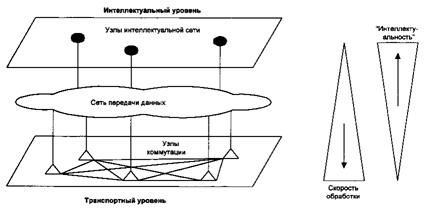
... сети телекоммуникаций, а также сравнивая технические возможности оборудований различных фирм в настоящем дипломном проекте предлагаю создать интеллектуальную сеть в г.Кокшетау на базе оборудования S-12 фирмы Alcatel [6]. Выбор оборудования не случаен, так как на сети города полностью эксплуатируется данная система. Это позволяет оптимально решить вопросы по синхронизации, сигнализации и по ...
элементы теории нечетких множеств можно применять для решения экономических задач в условиях неопределённости. 1. применение Логических функций 1.1 Применение методов дискретной математики в экономике При исследовании, анализе и решении управленческих проблем, моделировании объектов исследования и анализа широко используются методы формализированного представления, являющегося предметом ...
... реализуется тем лучше, чем четче будет организовано выполнение всех работ по подготовке и обеспечению перевозочного процесса. Однако организация автомобильных перевозок грузов из одной страны в другую - процесс сложный, требующий соблюдения международных конвенций и соглашений по перевозкам и транзиту, высокого качества обслуживания, точного исполнения условий контракта, соблюдения таможенных и ...
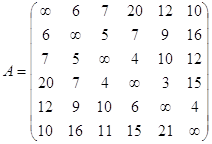


0 комментариев