Навигация
Численное решение показательного примера
3. Численное решение показательного примера
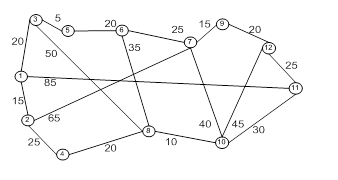
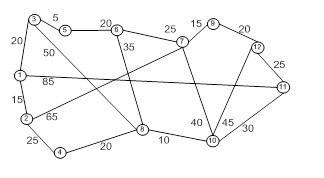
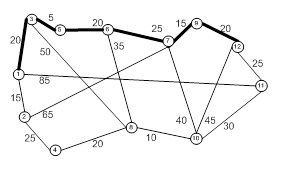
Найдем для сети, показанной на рисунке 5, кратчайшие пути между любыми двумя узлами. Расстояния между узлами этой сети проставлены на рисунке возле соответствующих ребер. Ребро (3,5) ориентировано, поэтому не допускается движение от узла 5 к узлу 3. Все остальные ребра допускают движение в обе стороны.
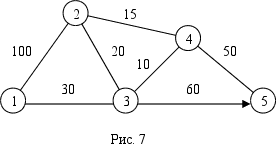
Шаг 0. Начальное решение матрицы D0 и S0 строятся непосредственно по заданной схеме
сети. Матрица D0 симметрична, за исключением пары элементов d35 и d53, где d35 = ∞ (поскольку невозможен переход от узла 5 к узлу 3).
| рис. 8
|
|
Шаг 1. В матрице D0 выделены ведущие строка и столбец (k=1) (рис. 8). После этого каждый элемент проверяется с помощью треугольного оператора. Таким образом, чтобы на основе матриц D0 и S0 получить матрицы D1 и S1, выполняем следующие действия:
проверяем d32 > d31 + d12 = 20 > 30 + 100 = 20 > 130 если условие принимает истину, то устанавливаем S32 = 1 ,а если нет тогда все так и остается.
Матрицы D1 и S1 имеют следующий вид (см. рис. 9):
| рис. 9
|
|
Шаг 2. Полагаем k=2. Треугольный оператор применяется к элементам матриц D1 и S1,
выделенным двойной рамкой. В результате получаем матрицы D2 и S2 (см. рис.10):
| рис. 10
|
|
Шаг 3. Полагаем k=3. В матрице D2 и S2 выделены ведущие строка и столбец.
Треугольный оператор применяется к элементам матриц D2 и S2, выделенные двойной рамкой. В результате получаем матрицы D3 и S3(см. рис.11):
| рис. 11
|
|
Шаг 4. Полагаем k=4. Выделены ведущие строка и столбец в матрице D3 и S3.
Получаем новые матрицы (см. рис.12):
| рис. 12
|
|
Шаг 5. Полагаем k=4. Ведущие строка и столбец в матрице D4 и S4 выделены. Никаких
действий на этом этапе не выполняем; вычисления закончены.
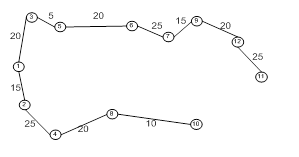
Конечные матрицы D4 и S4 содержат всю информацию, необходимую для определения кратчайших путей между любыми двумя узлами сети.
Для нахождения соответствующих маршрутов напомним, что сегмент маршрута (i,j) состоит из ребра (i,j) только в том случае, когда sij=j. В противном случае узлы i и j связаны, по крайней мере, через один промежуточный узел.
Похожие работы
... данных будет нести больше смысла, если его отсортировать каким‑либо образом. Часто требуется сортировать данные несколькими различными способами. Во‑вторых, многие алгоритмы сортировки являются интересными примерами программирования. Они демонстрируют важные методы, такие как частичное упорядочение, рекурсия, слияние списков и хранение двоичных деревьев в массиве. Наконец, сортировка ...
... сети телекоммуникаций, а также сравнивая технические возможности оборудований различных фирм в настоящем дипломном проекте предлагаю создать интеллектуальную сеть в г.Кокшетау на базе оборудования S-12 фирмы Alcatel [6]. Выбор оборудования не случаен, так как на сети города полностью эксплуатируется данная система. Это позволяет оптимально решить вопросы по синхронизации, сигнализации и по ...
элементы теории нечетких множеств можно применять для решения экономических задач в условиях неопределённости. 1. применение Логических функций 1.1 Применение методов дискретной математики в экономике При исследовании, анализе и решении управленческих проблем, моделировании объектов исследования и анализа широко используются методы формализированного представления, являющегося предметом ...
... реализуется тем лучше, чем четче будет организовано выполнение всех работ по подготовке и обеспечению перевозочного процесса. Однако организация автомобильных перевозок грузов из одной страны в другую - процесс сложный, требующий соблюдения международных конвенций и соглашений по перевозкам и транзиту, высокого качества обслуживания, точного исполнения условий контракта, соблюдения таможенных и ...
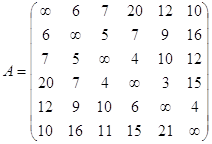


0 комментариев