Навигация
0 X 5
Решение задачи численным методом
Инициализация Решение Комментарий
X : = 0 root(V(X) - VO, X) = 0.297 Плоский ящик
X : = 1 root(V(X) - VO, X) = 1.5 Глубокий ящик
X : = 4 root(V(X) - VO, X) = 4.203 Решение физически
нереально (X > W/2)
Конструирование железного ящика максимального объёма
X : = 1 Инициализация
Given Начало блока решения
V(X) : = (L - 2X)Ч(W - 2X)ЧX Основное уравнение
V(X) » 100 Объём, заведомо превышающий
требуемый
X M : = minerr ( X ) Поиск оптимального значения Х
X M = 0.848 Найденное оптимальное значение Х
V(X M ) = 12.317 Максимально возможный объём ящика
Документ 2. Задача о конструирование железного ящика заданного и максимального
объёма
Задание мнимой единицы
i : = Ц-1
Арифметические операции
Z1 : = 2 + 3i Z2 : = 4 + 5i
Z : = Z1 + Z2 Z = 6 + 8i
Re ( Z ) = 6 Im ( Z ) = 8
sin ( Z1 ) = 9.154 - 4. 169i
Вычисление комплексных корней квадратного уравнения
х : = 0 + 3i ( Инициализация первого корня )
2
root(x + 2x +15, x) = - 1 + 3.742i ( Первый корень )
x : = 0 - 3i ( Инициализация второго корня )
2
root(x + 2x +15, x) = - 1 + 3.742i ( Второй корень )
Решение систем линейных уравнений с комплексными коэффициентами
й10 + 200i 0 - 200i щ й5 + 0iщ
А : =к ъ B : = к ъ
л0 - 200i 0 + 170iы л0 + 0iы
-1
X : = A B (Решение с помощью матричных операторов)
й0.037 + 0.131i щ
Х : =к ъ (Вектор решения)
л0.044 + 0.154i ы
Вычисление комплексного кругового интеграла
1
f(x) : = ѕ z(t) : = cos(t) + sin(t)
x
-4
te : = 6.2832 TOL : = 10 (Погрешность)
te
у йd щ
фf(z(t))к ѕ z(t)ъ dt = 6.283
лdt ы
0
Документ 3. Примеры операций с комплексными числами.
Задание ВАХ туннельного диода
0 0
.2 50 ( Векторы исходных данных,
.4 20 содержащие координаты
U: = .6 I : = 3 семи узловых точек ВАХ )
.8 4
1.0 14
1.2 55
Линейная интерполяция ВАХ
linterp(U, I, 0.15 ) = 37.5 (Примеры интерполяции ВАХ)
linterp(U , I, 0.5) = 11.5
J(V) : = linterp(U, I, V) (Задание функции J(V) ВАХ )
V : = -0.05, - 0.025 .. 1.2
40 На графике ВАХ при линейной
интерполяции отчётливо видны
отрезки прямых, и кривая В АХ
J(V),0 неестественно
-40
-0.05 V 1.2
Интерполяция кубическими сплайнами
IS : = cspline(U ,I) (Векторы вторых производных)
interp (IS, U, I, 0.15) = 49.493 (Примеры сплайн - интерполяции)
interp (IS, U, I, 0.5) = 8.191
J(V) : = interp (IS, U, I, V ) (Задание функции J(V) ВАХ)
V : = -0.05, - 0.025 .. 1.2
40 Кривая ВАХ при сплайн -
интерполяции отличается
плавностью и похожа на
J(V),0 реальную кривую ВАХ
-40
-0.05 V 1.2
Документ 4. Линейная и сплайн - интерполяция N - образной вольтамперной характеристики (ВАХ) туннельного диода .
Генерация 200 случайных чисел с равномерным распределением
i : = 1..200 x : = rnd ( 10 )
i
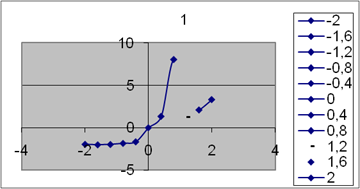
Графическое представление случайных чисел
10
х График наглядно показывает
i равномерность распределения
случайных чисел
0
Похожие работы
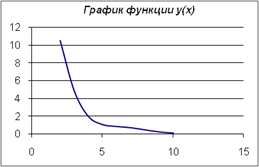
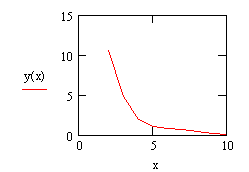
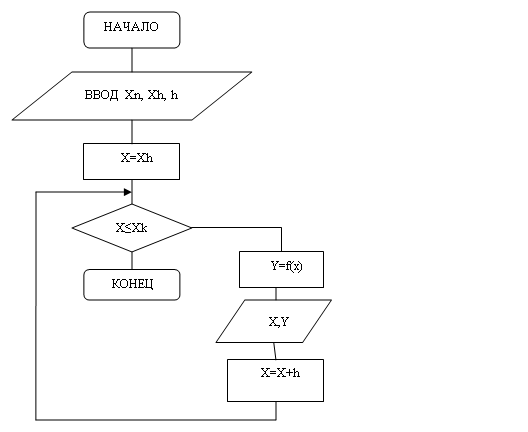
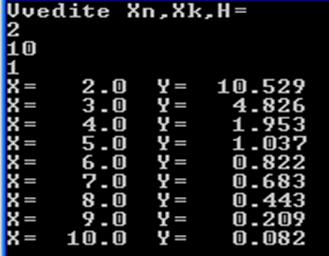
... 1,' Y=',Y: 8: 3); X: =X+H; until X>=Xk+H/2; readkey; end. Блок-схема к заданию: Результаты вычислений: Задание 1 (б) Решение программы вычисления функции с условием Решение уравнения в табличном редакторе Microsoft Excel Для реализации задачи необходимо использовать логическую функцию ЕСЛИ, которая возвращает одно значение, если заданное условие при вычислении дает ...
... іальних рівнянь у частинних похідних; - статистична обробка даних (інтерполяція, екстраполяція, апроксимація та багато іншого); - робота з векторами та матрицями (лінійна алгебра та ін.); - пошук мінімумів та максимумів функціональних залежностей; - пакет MathCAD доповнений довідником по основним математичним та фізико-хімічним формулам та константам, які можливо автоматично переносити у ...
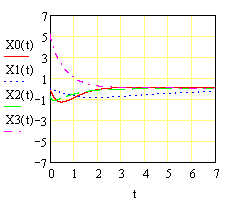
... мы будем определять аналитические зависимости изменения переменных состояния системы численными методами с использованием переходной матрицы, а также с помощью специальных функций MATHCAD. 2.2 Теоретическое обоснование применения преобразования Лапласа Классический метод решения системы дифференциальных уравнений высокого порядка связан с большими вычислительными затратами, особенно при ...
... со строками и столбцами матрицы 2.3.13 Объединение матрицы с вектором и матрицы с матрицей 2.3.14 Сортировка элементов вектора и матрицы 2.3.15 Разложение матрицы на треугольную, ортогональную 2.4 Использование матричных функций 2.4.1 Собственные значения и векторы собственных значений матрицы 2.4.2 Нахождение матрицы векторов собственных значений матрицы 2.4.3 Приведение заданной матрицы к ...



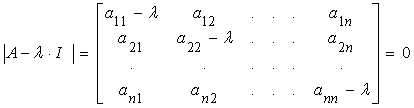
0 комментариев