Навигация
Графическое представление данных в статистике
ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ СТАТИСТИЧЕСКИХ ДАННЫХ
5.1. ПОНЯТИЕ О СТАТИСТИЧЕСКОМ ГРАФИКЕ. ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОГО ГРАФИКА
Современную науку невозможно представить без применения графиков. Они стали средством научного обобщения.
Выразительность, доходчивость, лаконичность, универсальность, обозримость графических изображений сделали их незаменимыми в исследовательской работе и в международных сравнениях и сопоставлениях социально-экономических явлений.
Впервые о технике составления статистических графиков упоминается в работе английского экономиста У. Плейфейра "Коммерческий и политический атлас", опубликованной в 1786 г. и положившей начало развитию приемов графического изображения статистических данных.
Трактовка графического метода как особой знаковой системы -искусственного знакового языка - связана с развитием семиотики, науки о знаках и знаковых системах.
Знак в семиотике служит символическим выражением некоторых явлений, свойств или отношений.
Существующие в семиотике знаковые системы принято разделять на неязыковые и языковые.
Неязыковые знаковые системы дают представление о явлениях окружающего нас мира (например, шкала измерительного прибора, высота столбика ртути в термометре и т. д.).
Языковые знаковые системы выполняют сигнальные функции, а также задачи сопоставления совокупностей явлений и их анализа. Характерно, что в этих системах сочетание знаков приобретает смысл только тогда, когда их объединение производится по определенным правилам.
В языковых знаковых системах различают естественные и искусственные системы знаков, или языков.
С точки зрения семиотики человеческая речь, выраженная знаками-буквами, составляет естественный язык.
Искусственные языковые системы используются в различных областях жизни и техники. К ним относятся системы математических, химических знаков, алгоритмические языки, графики и др.
Не исключая естественного языка, искусственные, или символические языки упрощают изложение специальных вопросов определенной области знаний.
Таким образом, статистический график - это чертеж, на котором статистические совокупности, характеризуемые определенными показателями, описываются с помощью условных геометрических образов или знаков. Представление данных таблицы в виде графика производит более сильное впечатление, чем цифры, позволяет лучше осмыслить результаты статистического наблюдения, правильно их истолковать, значительно облегчает понимание статистического материала, делает его наглядным и доступным. Это, однако, вовсе не означает, что графики имеют лишь иллюстративное значение. Они дают новое знание о предмете исследования, являясь методом обобщения исходной информации.
Значение графического метода в анализе и обобщении данных велико. Графическое изображение прежде всего позволяет осуществить контроль достоверности статистических показателей, так как, представленные на графике, они более ярко показывают имеющиеся неточности, связанные либо с наличием ошибок наблюдения, либо с сущностью изучаемого явления. С помощью графического изображения возможны изучение закономерностей развития явления, установление существующих взаимосвязей. Простое сопоставление данных не всегда дает возможность уловить наличие причинных зависимостей, в то же время их графическое изображение способствует выявлению причинных связей, в особенности в случае установления первоначальных гипотез, подлежащих затем дальнейшей разработке. Графики также широко используются для изучения структуры явлений, их изменения во времени и размещения в пространстве. В них более выразительно проявляются сравниваемые характеристики и отчетливо видны основные тенденции развития и взаимосвязи, присущие изучаемому явлению или процессу.
При построении графического изображения следует соблюдать ряд требований. Прежде всего график должен быть достаточно наглядным, так как весь смысл графического изображения как метода анализа в том и состоит, чтобы наглядно изобразить статистические показатели. Кроме того, график должен быть выразительным, доходчивым и понятным. Для выполнения вышеперечисленных требований каждый график должен включать ряд ос-ковных элементов: графический образ; поле графика;
пространственные ориентиры; масштабные ориентиры; экспликацию графика.
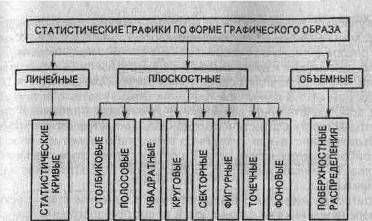
Рассмотрим подробнее каждый из указанных элементов. Графический образ (основа графика) - это геометрические знаки т. е. совокупность точек, линий, фигур, с помощью которых изображаются статистические показатели. Важно правильно выбрать графический образ, который должен соответствовать цели графика и способствовать наибольшей выразительности изображаемых статистических данных. Графическими являются лишь те образы, в которых свойства геометрических знаков - фигура, размер линий, расположение частей - имеют существенное значение для выражения содержания изображаемых статистических величин, причем каждому изменению выражаемого содержания соответствует изменение графического образа.
Поле графика - это часть плоскости, где расположены графические образы. Поле графика имеет определенные размеры, которые зависят от его назначения.
Пространственные ориентиры графика задаются в виде системы координатных сеток. Система координат необходима для размещения геометрических знаков в поле графика. Наиболее распространенной является система прямоугольных координат (рис. 5.18). Для построения статистических графиков используется обычно только первый и изредка первый и четвертый квадраты. В практике графического изображения применяются также полярные координаты. Они необходимы для наглядного изображения циклического движения во времени. В
рис 5.1
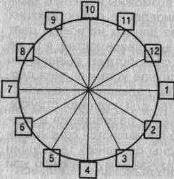
полярной системе координат (рис. 5.1) один из лучей, обычно правый горизонтальный, принимается за ось координат, относительно которой определяется угол луча. Второй координатой считается ее расстояние от центра сетки, называемое радиусом. В радиальных графиках лучи обозначают моменты времени, а окружности -величины изучаемого явления. На статистических картах пространственные ориентиры задаются контурной сеткой (контуры рек, береговая линия морей и океанов, границы государств) и определяют те территории, к которым относятся статистические величины.
Масштабные ориентиры статистического графика определяются масштабом и системой масштабных шкал. Масштаб статистического графика - это мера перевода числовой величины в графическую.
Масштабной шкалой называется линия, отдельные точки которой могут быть прочитаны как определенные числа. Шкала имеет большое значение в графике и включает три элемента: линию (или носитель шкалы), определенное число помеченных черточками точек, которые расположены на носителе шкалы в определенном порядке, цифровое обозначение чисел, соответствующих отдельным помеченным точкам. Как правило, цифровым обозначением снабжаются не все помеченные точки, а лишь некоторые из них, расположенные в определенном порядке. По правилам числовое значение необходимо помещать строго против соответствующих точек, а не между ними (рис. 5.2).
Рис. 5.2. Числовые интервалы
Носитель шкалы может представлять собой как прямую, так и кривую линии. Поэтому различают шкалы прямолинейные (например, миллиметровая линейка) и криволинейные - дуговые и круговые (циферблат часов).
Графические и числовые интервалы бывают равными и неравными. Если на всем протяжении шкалы равным графическим интервалам соответствуют равные числовые, такая шкала называется равномерной. Когда же равным числовым интервалам соответствуют неравные графические интервалы и наоборот, шкала называется неравномерной.
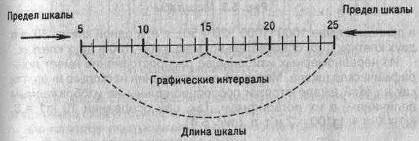
Масштабом равномерной шкалы называется длина отрезка (графический интервал), принятого за единицу и измеренного в каких-либо мерах. Чем меньше масштаб (рис. 5.3), тем гуще располагаются на шкале точки, имеющие одно и то же значение. Построить шкалу -это значит на заданном носителе шкалы разместить точки и обозначить их соответствующими числами согласно условиям задачи.
Как правило, масштаб определяется примерной прикидкой возможной длины шкалы и ее пределов. Например, на поле в 20 клеток надо построить шкалу от 0 до 850. Так как 850 не делится удобрю на 20, то округляем число 850 до ближайшего удобного числа,
Рис. 5.3. Масштабы
в данном случае 1000 (1000 : 20 = 50), т. е. в одной клетке 50, а в двух клетках 100; следовательно, масштаб - 100 в двух клетках.
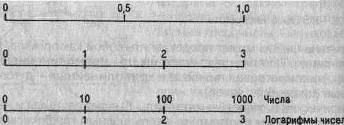
Из неравномерных наибольшее распространение имеет логарифмическая шкала. Методика ее построения несколько иная, так как на этой шкале отрезки пропорциональны не изображаемым величинам, а их логарифмам. Так, при основании 10 1д1 = О-1д1 = 0 = 1; 1д100 = 2 и т. д. (рис. 5.4).
Последний элемент графика - экспликация. Каждый график должен иметь словесное описание его содержания. Оно включает в себя название графика, которое в краткой форме передает его содержание; подписи вдоль масштабных шкал и пояснения к отдельным частям графика.
Похожие работы
... возложены обязанности по организации ведения судебной статистики и составлению отдельных отчетов. Указанные лица подписывают статистические отчеты. 4. Табличный и графический метод представления данных судебной статистики Результаты сводки и группировки материалов статистического наблюдения, как правило, представляются в виде статистических таблиц - систематизированного, рационального ...
... . 4 1 - 3 9 Статистическое изучение динамики правовых явлений (ряды динамики в правовой статистике). 4 - - 4 10 Статистические методы изучения взаимосвязей. Комплексный статистический анализ. 4 - - 4 ИТОГО: 40 6 2 32 2.3 Учебная программа дисциплины Содержание лекционного курса Тема 1. Общее понятие статистики и ее отраслей. Современная организация статистики в ...
... графически изобразить уровень концентрации явления. Пример построения кривой Лоренца описан в главе 9. 6. СТАТИСТИЧЕСКИЕ КАРТЫ Статистические карты представляют собой вид графических изображений статистических данных на схематической географической карте, характеризующих уровень или степень распространения того или иного явления на определенной территории. Средствами изображения ...
... Для унимодальных симметричных распределений почти 70% значений лежит в интервале . Свойства дисперсии: 1. Влияние на дисперсию увеличения каждого значения на какую либо константу: , после выполнения математических операций убеждаемся, что дисперсия не изменяется. 2. Изменение дисперсии при умножении каждого исходного значения на константу: , то есть дисперсия увеличивается на квадрат константы. ...

0 комментариев