Навигация
5.5. ДИАГРАММЫ ДИНАМИКИ
Для изображения и внесения суждений о развитии явления во времени строятся диаграммы динамики.
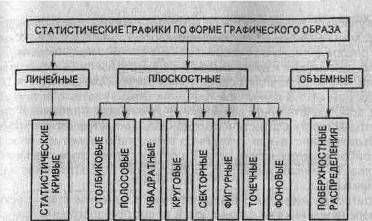
Для наглядного изображения явлений в рядах динамики используются диаграммы: столбиковые, ленточные, квадратные, круговые, линейные, радиальные и др. Выбор вида диаграммы зависит в основном от особенностей исходных данных, цели исследования. Например, если имеется ряд динамики с несколькими неравноотстоящими уровнями во времени (1913, 1940, 1950, 1980, 1985, 1997 гг.), то часто для наглядности используют столбиковые, квадратные или круговые диаграммы. Они зрительно впечатляют, хорошо запоминаются, но не годны для изображения большого числа уровней, так как громоздки. Когда число уровней в ряду динамики велико, целесообразно применять линейные диаграммы, которые воспроизводят непрерывность процесса развития в виде непрерывной ломаной линии. Кроме того, линейные диаграммы удобно использовать: если целью исследования является изображение общей тенденции и характера развития явления; когда на одном графике необходимо изобразить несколько динамических рядов с целью их сравнения; если наиболее существенным является сопоставление темпов роста, а не уровней.
Для построения линейных графиков применяют систему прямоугольных координат. Обычно по оси абсцисс откладывается время (годы, месяцы и т. д. ), а по оси ординат - размеры изображаемых явлений или процессов. На оси ординат наносят масштабы. Особое внимание следует обратить на их выбор, так как от этого зависит общий вид графика. Обеспечение равновесия, пропорциональности между осями координат необходимо в графике в связи с тем, что нарушение равновесия между осями координат дает неправильное изображение развития явления;
Если масштаб для шкалы на оси абсцисс очень растянут по сравнению с масштабом на оси ординат, то колебания в динамике явлений мало выделяются, и наоборот, преувеличение масштаба по оси ординат по сравнению с масштабом на оси абсцисс дает резкие колебания. Равным периодам времени и размерам уровня должны соответствовать равные отрезки масштабной шкалы.
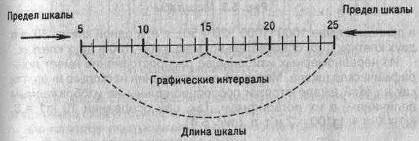
В статистической практике чаще всего применяются графические изображения с равномерными шкалами. По оси абсцисс они берутся пропорционально числу периодов времени, а по оси ординат - пропорционально самим уровням. Масштабом равномерной шкалы будет длина отрезка, принятого за единицу.
рассмотрим построение линейной диаграммы на основании следующих данных (табл. 5.7).
Таблица 5.7
Динамика валового сбора зерновых культур в регионе за 1985-1994 гг.
| Год | 1985 | 1986 | 1987 | 1988 | 1989 | 1990 | 1991 | 1992 | 1993 | 1994 |
| Млн.т | 237,4 | 179,2 | 189,1 | 158,2 | 186,8 | 192,2 | 172,6 | 191,7 | 210,1 | 211,3 |
Изображение динамики валового сбора зерновых культур на координатной сетке с неразрывной шкалой значений, начинающихся от нуля, вряд ли целесообразно, так как 2/3 поля диаграммы остаются неиспользованными и ничего не дают для выразительности изображения. Поэтому в данных условиях рекомендуется строить шкалу без вертикального нуля, т. е. шкала значений разрывается недалеко от нулевой линии и на диаграмму попадает лишь часть всего возможного поля графика. Это не приводит к искажениям в изображении динамики явления, и процесс его изменения рисуется диаграммой более четко (рис. 5.18).
Рис. 5.18. Динамика валового сбора зерновых культур в регионе за 1985-1994 гг.
Нередко на одном линейном графике приводится несколько кривых, которые дают сравнительную характеристику динамики различных показателей или одного и того же показателя.
Примером графического изображения сразу нескольких показателей является рис. 5.19.
141
Рис. 5.19. Динамика производства чугуна и готового проката в регионе за 1985-1994 гг.
Однако на одном графике не следует помещать более трех-четырех кривых, так как большое их количество неизбежно осложняет чертеж и линейная диаграмма теряет наглядность.
В некоторых случаях нанесения на один график двух кривых дает возможность одновременно изобразить динамику третьего показателя, если он является разностью первых двух. Например, при изображении динамики рождаемости и смертности площадь между двумя кривыми показывает величину естественного прироста или естественной убыли населения.
Иногда необходимо сравнить на графике динамику двух показателей, имеющих различные единицы измерения. В таких случаях понадобится не одна, а две масштабные шкалы. Одну из них размещают справа, другую - слева.
Однако такое сравнение кривых не дает достаточно полной картины динамики этих показателей, так как масштабы произвольны. Поэтому сравнение динамики уровня двух разнородных показателей следует осуществлять на основе использования одного масштаба после преобразования абсолютных величин в относительные. Примером такой линейной диаграммы является рис. 5.20.
Линейные диаграммы с равномерной шкалой имеют один недостаток, снижающий их познавательную ценность: равномерная шкала позволяет измерять и сравнивать только отраженные на диаграмме абсолютные приросты или уменьшения показателей на протяжении исследуемого периода. Однако при изучении динамики важно знать относительные изменения исследуемых показателей по сравнению с достигнутым уровнем или темпы их измене-
Рис. 5.20. Доли вкладов граждан в Сбербанк и коммерческие банки в одном из городов в 1995 г. (%)
ния. Именно относительные изменения экономических показателей в динамике искажаются при их изображении на координатной диаграмме с равномерной вертикальной шкалой. Кроме того, в обычных координатах теряет всякую наглядность и даже становится невозможным изображение для рядов динамики с резко изменяющимися уровнями, которые обычно имеют место в динамических рядах за длительный период времени.
В этих случаях следует отказаться от равномерной шкалы и положить в основу графика полулогарифмическую систему. Основная идея полулогарифмической системы состоит в том, что в ней равным линейным отрезкам соответствуют равные значения логарифмов чисел. Такой подход имеет преимущество: возможность уменьшения размеров больших чисел через их логарифмические эквиваленты. Однако с масштабной шкалой в виде логарифмов график малодоступен для понимания. Необходимо рядом с логарифмами, обозначенными на масштабной шкале, проставить сами числа, характеризующие уровни изображаемого ряда динамики, которые соответствуют указанным числам логарифмов. Такого рода графики носят название графиков на полулогарифмической сетке.
Полулогарифмической сеткой называется сетка, в которой на одной оси нанесен линейный масштаб, а на другой - логарифмический. В данном случае логарифмический масштаб наносится на ось ординат, а на оси абсцисс располагают равномерную шкалу для отсчета времени по принятым интервалам (годам, кварталам, месяцам, дням и пр.).
Техника построения логарифмической шкалы следующая (рис. 5.21).
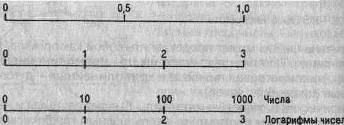
Рис. 5.21. Схема логарифмического масштаба
Необходимо найти логарифмы исходных чисел, начертить ординату и разделить ее на несколько равных частей. Затем нанести на ординату (или равную ей параллельную линию) отрезки, пропорциональные абсолютным приростам этих логарифмов. Далее записать соответствующие логарифмы чисел и их антилогарифмы, например (0,000; 0,3010; 0,4771; 0,6021; ...; 1,000, что дает 1, 2, 3, 4, ..., 10). Полученные антилогарифмы окончательно дают вид искомой шкалы на ординате.
Приведем пример логарифмического масштаба. : Допустим, что надо изобразить на графике динамику производства электроэнергии в регионе за 1965-1994 гг., за эти годы оно выросло в 9,1 раза. С этой целью находим логарифмы для каждого уровня ряда (табл. 5.8).
' Определив минимальное и максимальное значение логарифмов производства электроэнергии, построим масштаб с таким расчетом, чтобы все данные разместились на графике.
Учитывая масштаб, находим соответствующие точки, которые соединим прямыми линиями, в результате получим график (рис. 5.22) с использованием логарифмического масштаба на оси ординат. Он называется диаграммой на полулогарифмической сетке. Полной логарифмической диаграммой он станет в том случае, если по оси абсцисс будет построен логарифмический масштаб. В ря
Таблица 5.8
Динамика производства электроэнергии в регионе за 1965 -1994 гг. (млрд. кВт.ч)
| Год | У | 1-дУ, | Год | У, | 1-9У, |
| 1965 1970 1975 | 170 292 507 | 2,23 2,46 2,70 | 1985 1990 1994 | 1039 1294 1544 | 3,02 3,11 3,19 |
| 1980 | 741 | 2,84 |
Рис. 5.22. Динамика производства электроэнергии в регионе за 1965-1994 гг.
дах динамики это никогда не применяется, так как логарифмирование времени лишено всякого смысла.
Применяя логарифмический масштаб, можно без всяких вычислений характеризовать динамику уровня. Если кривая на логарифмическом масштабе несколько отклонена от прямой и становится вогнутой к оси абсцисс, значит, имеет место падение темпов; когда кривая в своем течении приближается к прямой - стабильность темпов; если она отклоняется от прямой в сторону, выпуклую к оси абсцисс, изучаемое явление имеет тенденцию к росту с увеличивающимися темпами.
Динамику изображают и радиальные диаграммы, строящиеся в полярных координатах. Радиальные диаграммы преследуют цель наглядного изображения определенного ритмического Движения во времени. Чаще всего эти диаграммы применяются Для иллюстрации сезонных колебаний. Радиальные диаграммы разделяются на замкнутые и спиральные. По технике построения радиальные диаграммы отличаются друг от друга в зависимости от того, что взято в качестве пункта отсчета - центр круга или окружность.
Замкнутые диаграммы отражают внутригодичный цикл динамики какого-либо одного года. Спиральные диаграммы показывают внутригодичный цикл динамики за ряд лет.
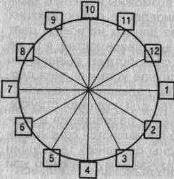
Построение замкнутых диаграмм сводится к следующему: вычерчивается круг, среднемесячный показатель приравнивается к радиусу этого круга. Затем весь круг делится на 12 радиусов, которые на графике приводятся в виде тонких линий. Каждый радиус обозначает месяц, причем расположение месяцев аналогично циферблату часов: январь - в том месте, где на часах 1, февраль - 2, и т. д. На каждом радиусе делается отметка в определенном месте согласно масштабу исходя из данных за соответствующий месяц. Если данные превышают среднемесячный уровень, отметка делается за пределами окружности на продолжении радиуса. Затем отметки различных месяцев соединяются отрезками. В приведенном примере (рис. 5.23) К = 44,8 тыс. т, длина радиуса - 3,0 см. Следовательно, 1 см = 44,8 : 3,0 " 15 тыс. т. Данная замкнутая диаграмма наглядно показывает, что производство мяса подвергнуто сезонным колебаниям. Минимум
Рис. 5.23. Сезонные колебания производства мяса в одном из регионов России в 1994 г.
производства мяса приходится на апрель, май, затем наблюдается медленное его повышение к августу, резкий подъем в сентябре, октябре и опять спад в декабре, январе. Если же в качестве базы для отсчета взять не центр круга, а окружность, то диаграммы называются спиральными.
Построение спиральных диаграмм отличается от замкнутых тем, что в них декабрь одного года соединяется не с январем данного же года, а с январем следующего года. Это дает возможность изобразить весь ряд динамики в виде спирали. Особенно наглядна такая диаграмма, когда наряду с сезонными изменениями происходит неуклонный рост из года в год (рис. 5.24).
Рис. 5.24. Продажа пива в розничной торговле в городе за 1992 - 1994 гг.
Среди различных видов графиков особое место занимает кривая, именуемая моделью Лоренца, или кривой Лоренца. Данная кривая дает возможность графически изобразить уровень концентрации явления. Пример построения кривой Лоренца описан в главе 9.
Похожие работы
... возложены обязанности по организации ведения судебной статистики и составлению отдельных отчетов. Указанные лица подписывают статистические отчеты. 4. Табличный и графический метод представления данных судебной статистики Результаты сводки и группировки материалов статистического наблюдения, как правило, представляются в виде статистических таблиц - систематизированного, рационального ...
... . 4 1 - 3 9 Статистическое изучение динамики правовых явлений (ряды динамики в правовой статистике). 4 - - 4 10 Статистические методы изучения взаимосвязей. Комплексный статистический анализ. 4 - - 4 ИТОГО: 40 6 2 32 2.3 Учебная программа дисциплины Содержание лекционного курса Тема 1. Общее понятие статистики и ее отраслей. Современная организация статистики в ...
... графически изобразить уровень концентрации явления. Пример построения кривой Лоренца описан в главе 9. 6. СТАТИСТИЧЕСКИЕ КАРТЫ Статистические карты представляют собой вид графических изображений статистических данных на схематической географической карте, характеризующих уровень или степень распространения того или иного явления на определенной территории. Средствами изображения ...
... Для унимодальных симметричных распределений почти 70% значений лежит в интервале . Свойства дисперсии: 1. Влияние на дисперсию увеличения каждого значения на какую либо константу: , после выполнения математических операций убеждаемся, что дисперсия не изменяется. 2. Изменение дисперсии при умножении каждого исходного значения на константу: , то есть дисперсия увеличивается на квадрат константы. ...

0 комментариев