Навигация
Следствие теорем сложения и умножения вероятностей
6. Следствие теорем сложения и умножения вероятностей.
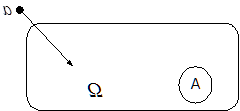
Площадь прямоугольника – это пространство элементарных всех событий. Площадь кругов Е1 и Е2 – числа исходов, благоприятствующих событиям Е1 и Е2.
- число исходов, благоприятствующих совместному появлению событий Е1 и Е2.
Допустим нас удовлетворяет появление только одного из двух событий Е1 и Е2. Если эти события не совместны, то их пересечение пустое множество Æ, а вероятность появления Е1 и Е2 несовместимых событий определяется по формуле:
.
Однако, при совместных событиях нас не удовлетворяет ситуация, когда оба события появляются одновременно. Вероятность такого исхода определяется по теореме умножения вероятностей.
Таким образом, вероятность появления событий Е1 и Е2 в общем случае можно рассчитать по формуле:
- для независимых событий.
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.
- для зависимых событий.
Пример: Два продавца независимо друг от друга обслуживают покупателей. Вероятность того, что первый продавец сумеет продать товар 0,3, а второй – 0,2. Какова вероятность того, что хотя бы один из продавцов реализует товар?
Данную задачу можно решить и другим способом, рассматривая события, как независимые совокупности. Тогда вероятность, что первый продавец не сумет продать товар – 0,7, а вероятность того, что второй не сумеет продать товар – 0,8.
Пример: Вероятность покупки мужского костюма посетителем магазина составляет 0,02, галстука – 0,1, а вероятность покупки галстука под приобретенный костюм - 0,3.
Надо определить вероятность покупки покупателями хотя бы одной из этих вещей.
Комбинация теорем сложения и умножения вероятностей выражается в формуле полной вероятности.
Вероятность события Е, которое может произойти только при появлении одного из событий , составляющих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события Е.
По условию достоверным является появление одного из событий или или или . По теореме умножения вероятностей:
Но так как все эти события не совместны, вероятность появления одного из них определяется по теореме сложения вероятностей.
Пример: На плодоовощную базу поступило 4 партии картофеля. В первой партии – 95% доля стандартных клубней, во второй – 97%, в третьей – 94%, в четвертой – 91%. При этом доля первой партии в общем объеме поставок – 28%, второй – 31%, третьей – 24%, четвертой – 17%. Определить вероятность того, что магазину, заказавшему товар, достанется стандартная продукция.
Полученный результат характеризует математическое ожидание или вероятность поставки стандартной продукции в магазин. Фактически это долевая средняя, показывающая среднюю долю стандартных клубней в четырех партиях.
7. Вероятность гипотез. Формула Байеса.
Как уже отмечалось, практически любое утверждение в статистике рассматривается как гипотеза, то есть некоторое предположение о наличии, форме, тесноте взаимосвязей.
Предположим, событие Е наступает только при появлении одного из несовместных событий , образующих полную группу. Допустим, в результате испытания событие Е произошло, то есть достоверным стало одно из событий или или или .
Каждое из этих событий рассматривается как гипотетическое и его вероятность как раз определяется по формуле Байеса.
Предыдущий пример: Известно, что в магазин поставлен стандартный картофель. Какова вероятность того, что он из четвертой партии.
Таким образом, только в 16-ти случаях из 100 доставленная в магазин стандартная продукция окажется из четвертой партии.
Применение формулы Байеса позволяет переоценить вероятности гипотез по результатам испытаний, в следствие которых появилось событие Е.
Достоинство формулы Байеса в том, что она может применяться при отсутствии сведений о числе элементарных исходов, достаточно знать вероятности или частости событий.
8. Независимые события. Биномиальное распределение.
Предположим событие Е во всех случаях имеет одну и ту же вероятность , тогда вероятность противоположного события будет так же постоянна и может определяться по формуле .
Такой подход позволяет рассматривать практически любое пространство элементарных событий, как дихотомное (то есть состоит из противоположных событий).
Допустим, необходимо определить вероятность появления события Е ровно k раз в n независимых испытаниях. В этом случае событие противоположное Е произойдет n-k раз. Отобрать k-элементов из n можно различными способами, каждый из которых несовместное событие, появление которого это результат игры случая.
В математике доказано, что число различных комбинаций из n элементов по k определяется по формуле:
, ! это произведение натурального ряда чисел, каждое из которых больше предыдущего на 1 (начиная с 1).
В соответствии с теоремой умножения вероятностей вероятность появления одной из возможных комбинаций определяется по формуле:
Формула, которая определяет вероятность появления события Е k-раз в n-независимых испытаниях, называется формулой Бернулли. А схема отбора из дихотомной совокупности схемой Бернулли (или схемой возвращаемого шара или схемой повторного отбора).
Пример: Для обслуживания покупателей супермаркета в час пик без очередей должно работать не менее 6 контролеров-кассиров из 8. Вероятность отсутствия одного из работников составляет 0,1. Найти вероятность работы расчетно-кассового узла без очередей.
Поскольку нас устраивает работа 6, 7, 8 кассовых кабин, то вероятность появления одного из этих несовместных событий будет определяться по формуле сложения вероятностей. Каждая из этих вероятностей может определяться по формуле Бернулли.
Таким образом, в 96 случаях из 100 очередей не будет.
Если при фиксированной численности n-повторного отбора из дихотомной совокупности изменять величину k, то полученное распределение вероятности будет называться биномиальным. Поскольку его ординаты представляют собой элементы разложения бинома .
Число наступления событий в n-независимых испытаниях называется наивероятнейшим, если этому числу соответствует наибольшая вероятность.
При этом если k смешанное число, то в результате выбирается ближайшее к этому смешанному числу, но меньше его, целое число.
В примере с кассирами .
Математическое ожидание М(k) числа появления событий Е в n-независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании.
Если перейти от абсолютного числа раз появления события к плотностям распределения вероятностей, то будет равно p.
Дисперсия биномиального распределения , - по плотности.
График биномиального распределения зависит от соотношения p и q. Если p равно q и равно 0,5, то распределение симметрично, в противном случае (p≠q) наблюдается асимметрия или скошенность полигона.
Показатель асимметрии биномиального распределения определяется по формуле:
Если , то высота биномиального распределения соответствует высоте кривой нормального распределения. Доказано, что с увеличением числа испытаний значения , а биномиальное распределение стремится к нормальному распределению.
Похожие работы
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... равна 0,515). Конец 19 в. и 1-я половина 20 в. отмечены открытием большого числа статистических закономерностей в физике, химии, биологии и т.п. Возможность применения методов теории вероятностей к изучению статистических закономерностей, относящихся к весьма далёким друг от друга областям науки, основана на том, что вероятности событий всегда удовлетворяют некоторым простым соотношениям, о ...
... {ξn (ω )}¥n=1 . Поэтому, во-первых, можно говорить о знакомой из математического анализа (почти) поточечной сходимости последовательностей функций: о сходимости «почти всюду», которую в теории вероятностей называют сходимостью «почти наверное». Определение 46. Говорят, что последовательность с. в. {ξn } сходится почти наверное к с. в. ξ при n ® ¥ , и пишут: ξn ...
... ничего другого, кроме как опять же события и . Действительно, имеем: *=, *=, =, =. Другим примером алгебры событий L является совокупность из четырех событий: . В самом деле: *=,*=,=,. 2.Вероятность. Теория вероятностей изучает случайные события. Это значит, что до определенного момента времени, вообще говоря, нельзя сказать заранее о случайном событии А произойдет это событие или нет. Только ...





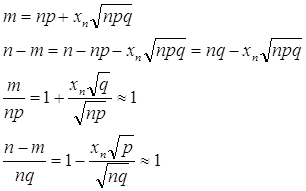
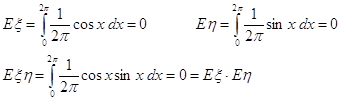
0 комментариев