Навигация
Исходя из принципа стандартного отклонения: Н(х)=b*(x), (b>0) – страховая надбавка прямо пропорциональна отклонению от среднего значения ущерба
2. Исходя из принципа стандартного отклонения: Н(х)=b*(x), (b>0) – страховая надбавка прямо пропорциональна отклонению от среднего значения ущерба.
3. По коэффициенту вариации: Н(х)=с*Var(x), (с>0), то есть страховая надбавка напрямую зависит от стандартного отклонения, и изменяется обратно пропорционально от его среднего значения.
(a,b,c) – числа, показывающие степень пропорциональности и уровень страховой надбавки.
Нетто-премию можно представить не только как математическое ожидание величины ущербов, но и как произведение среднего ущерба на значение вероятности его появления в различных временных периодах: Е1(Х)=, где t – временные периоды. Данная формула имеет смысл, если страховые события независимы, то есть наступление одного из них не влияет на появление другого. В принципе, эта формула также выражает принцип финансовой эквивалентности: нетто-премия равна произведению средней величины ущерба (так для себя ее оценивает страхователь) заранее известной вероятности его наступления (определенной на основании прошлого опыта).
Для определения страховой премии необходимо знать, что страховая премия уплачивается во время заключения договора страхования, а страховая сумма – спустя некоторое время (если произойдет страховой случай). Поэтому у страховщиков есть и запас времени, и возможность получить всю премию целиком, не заплатив ничего страхователю. Используя время, страховщик может инвестировать средства, получая от этого дополнительный доход. А если не произойдет страховой случай, то сумма страховых премий по данным договорам страхования остается у страховщика. В этих двух пунктах и заключаются основные доходы страховой компании.
Страховой бизнес обладает значительной долей авантюризма, в нем неотъемлемо присутствует элемент случайности. То есть, как страховщик, так и страхователь получают свои выгоды в зависимости от фортуны. Если рассмотреть формирование цены страховой услуги с точки зрения затрат, то их определение заключается в калькуляции ущерба, к которому приведет страховое событие. Его определяют как страховщик, так и страхователь, договариваясь о выплате определенной страховой суммы. Однако, в страховании нельзя определить придется ли нести эти затраты страховщику, как компании, оказывающей услуги. В данном случае сложно найти равновесную цену и определить взносы страхователя. Единственным путем в ее определении является анализ прошлых данных, при этом исследуемый период должен быть как можно дольше, а совокупность данных однороднее.
Величина выплат по договору страхования является случайной величиной, а, следовательно, сумма выплат по всем договорам, также величина случайная. Сумма выплат ограничена страховым фондом, который формируется из страховых премий. Поэтому совокупная страховая сумма варьируется в некотором интервале, верхняя граница которого равна сумме всех выплат по всем договорам. Для обеспечения 100%-ной гарантии того, что сумма нетто-премий превысит сумму выплат, страховщик должен создать страховой фонд в размере совокупной страховой суммы. В этом случае страховая премия будет равна страховой сумме. В результате страхователь, с учетом нагрузки, должен будет заплатить больше, чем получит при наступлении страхового случая. Такие условия страхователь не примет, а, следовательно, страховщику приходится рисковать так, что его риск определяется вероятностью всех страховых событий от которых он страхует. Для себя страховщик определяет размер своего риска, что математически можно выразить следующим неравенством: или , где y – заданная страховщиком гарантия безопасности, Si – выплата, Pi - премия, b – верхняя граница страховой гарантии. Сущность данного неравенства такова: вероятность того, что сумма всех выплат превысит сумму всех взносов страхователей, должна быть определена страховщиком заранее. Это делается для определения нетто-премии.
Согласно теореме А.М.Ляпунова (если Х – случайная величина, равная сумме большого числа независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение близкое к нормальному) страховые события и страховые выплаты распределены по нормальному закону. Если известен закон распределения случайной величины, то приведенное выше неравенство легко решаемо. Во-первых, вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a,b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b (. Во-вторых, - функция нормального распределения, где a – матемпатическое ожидание случайной величины, а - ее среднее квадратическое отклонение. И в-третьих, , где Ф – функция Лапласа. Сумма нетто-премий является математическим ожиданием от суммы страховых выплат, а вероятность отклонения должна быть задана страховщиком заранее, то приведенное выше неравенство тождественно приведенному выше. Подставляя известные значения в данное уравнение можно найти суммарную величину нетто-премии.
Исходя из принципа финансовой эквивалентности, ожидаемую величину нетто-премии можно выразить как произведение страховой суммы и нетто-ставки, выражаемой в процентах (Е(X)=S(X)*T(X)/100). Где Т(Х) – нетто ставка, которая зависит как от вероятности наступления страхового случая, так и от тяжести страхового случая (величины ущерба). Страховую сумму определяет сам страхователь. Верхняя ее граница – максимальная стоимость страхуемого имущества.
Нетто-премия является частью брутто-премии (П(Х)), которую также можно выразить в процентах к общей величине выплат: П(Х) = S(X)*L(X)/100, где L(X) – брутто ставка в %. При этом, L(X) = Т(Х) *f , где f – доля нагрузки, выраженная в процентах. Доля нагрузки рассчитывается по данным бухгалтерского учета страховщика: , где R - расходы, за исключением комиссионных. - сумма собранных брутто-премий по данному виду страхования, K(%) – процент комиссионных, получаемых посредниками по данному виду страхования, V- доля прибыли в брутто-ставке, которую страховщик хочет получить по данному виду страхования. Исходя из приведенных выше формул, расчет брутто-ставки можно представить следующим выражением: П(Х)=Т(Х)/(1-f) или П(Х)=Т(Х)/100-f%.
Выше были описаны общие принципы формирования нетто-ставок, которые являются основой частных расчетов, зависящих от вида страхования. Каждый из видов имеет свои особенности, связанные с характером страхуемых событий и объектов. Некоторые из этих особенностей оказывают существенное влияние на расчет нетто-ставок.
Виды страхования сточки зрения особенностей расчета нетто-ставок можно разделить на 2 категории:
1. Страхование жизни. Здесь формирование резерва взносов и расчеты тарифных ставок производятся с помощью актуарных методов, на основе таблиц смертности и норм доходности по инвестициям временно свободных резервов по страхованию жизни.
2. Рисковые виды страхования. Это те виды страховой деятельности, отличающиеся от страхования жизни. Они не предусматривают обязательств страховщика по выплате страховой суммы при окончании срока действия договора страхования, и не связаны с накоплением страховой суммы в течении срока действия договора страхования. В рисковых видах страхования не используется принцип капитализации и, следовательно, при расчете нетто-ставок не используются методы финансовых исчислений (дисконтирование и компаундинг). Данные виды страховой деятельности можно условно разделить на два вида:
- Массовые рисковые виды страхования. Они охватывают значительное число субъектов страхования и страховых рисков, характеризующихся однородность объектов страхования и незначительным разбросом в размерах страховых сумм. Наличие большого числа застрахованных объектов подразумевает, что по указанным рискам существует достаточный объем статистических данных, на основе которых можно описать всю совокупность рисков с помощью их числовых характеристик, таких как среднее значение и дисперсия. При этом, учитывая однородность застрахованных объектов, можно утверждать, что средние значения будут характеризовать всю совокупность с достаточной точностью.
- Страхование редких событий и крупных рисков. В данном случае речь идет о рисках, связанных с низкой частотой наступления страхового события и высокой стоимостью ущерба. Число объектов, которое можно застраховать, ограничено, а разброс страховых сумм составляет значительную величину. Для страхования редких событий и крупных рисков существуют некоторые особенности расчета нетто-ставок, обусловленные спецификой страхуемых рисков и объектов. Во-первых, при расчете тарифов необходимо опираться на данные за несколько лет (чем больше срок тем точнее расчет). Определенная таким образом премия должна поддерживать финансовое равновесие страховщика в пределах не одного года, а достаточно продолжительного периода. Во-вторых, при расчетах нетто-премий необходимо использовать реальную стоимость риска, а не среднюю, в отличии от страхования массовых рисков, так как совокупность рисков неоднородна. В-третьих, страховщики вынуждены учитывать перестрахование на величину ущерба по всему портфелю рисков данного типа. В-четвертых, для взвешенного расчета тарифных ставок необходимо расширить базу данных за пределы статистической информации и использовать данные других страховых компаний.
Расчет тарифных ставок при страховании жизни.
Страхование жизни обуславливает ряд особенностей, которые влияют на выбор форм и методов анализа подготовки и проведения страховых операций. Можно выделить основные факторы, которые влияют на методику расчета тарифных ставок по страхованию жизни:
1. Объектом договора по данному виду страхования является жизнь, здоровье и трудоспособность граждан. Количественные показатели, характеризующие продолжительность жизни и смертность среди населения страны централизовано собираются и обрабатываются в федеральных и региональных органах статистики. На основании подобных данных составляются таблицы смертности, которые используются страховщиками при расчете нетто-ставок по страхованию жизни.
2. Договоры страхования жизни, обычно, заключаются на длительный срок. Период времени между уплатой взносов и моментом выплат достигает нескольких лет. В течении этого срока за счет инфляции и прибыли, получаемой от инвестирования временно свободных средств, стоимость страховых взносов изменяется. Чтобы учесть подобные изменения применяются методы финансовых исчислений (дисконтирование).
В страховании жизни неопределенность связана со случайным характером продолжительности человеческой жизни. Поэтому страховщики должны располагать данными для расчета вероятностей дожития до определенного возраста лиц различного пола. Источником таких данных являются таблицы смертности, составляемые на основе переписи населения.
Таблица смертности.
| Таблица смертности и коммутационных функций. (мужчины, i=9% | Аннуитет. | |||||||||
| x | lx | qx | dx | Dx | Nx | Cx | Mx | N(12)x | N(12)x | ax |
| 18 | 100000 | 0,00149 | 149 | 21199,37402 | 244591,9762 | 28,978961 | 1003,702 | 254308,36 | 234875,5965 | 11,53769805 |
| 19 | 99851 | 0,001732582 | 173 | 19419,98803 | 223392,6022 | 30,868544 | 974,7228 | 232293,43 | 214491,7744 | 11,50323069 |
| 20 | 99678 | 0,001956299 | 195 | 17785,63423 | 203972,6142 | 31,921122 | 943,8543 | 212124,36 | 195820,8652 | 11,46839137 |
| 21 | 99483 | 0,002161173 | 215 | 16285,1745 | 186186,98 | 32,289068 | 911,9332 | 193651,02 | 178722,9417 | 11,4329128 |
| 22 | 99268 | 0,002337108 | 232 | 14908,238 | 169901,8055 | 31,965281 | 879,6441 | 176734,75 | 163068,8631 | 11,39650477 |
| 23 | 99036 | 0,002494043 | 247 | 13645,31729 | 154993,5675 | 31,22202 | 847,6788 | 161247,67 | 148739,4637 | 11,35873679 |
| 24 | 98789 | 0,002631872 | 260 | 12487,41769 | 141348,2502 | 30,151637 | 816,4568 | 147071,65 | 135624,8504 | 11,3192538 |
| 25 | 98529 | 0,002770758 | 273 | 11426,19487 | 128860,8325 | 29,045155 | 786,3051 | 134097,84 | 123623,8265 | 11,27766802 |
| 26 | 98256 | 0,002931119 | 288 | 10453,70243 | 117434,6376 | 28,111048 | 757,26 | 122225,92 | 112643,3573 | 11,23378424 |
| 27 | 97968 | 0,003123469 | 306 | 9562,441641 | 106980,9352 | 27,401825 | 729,1489 | 111363,72 | 102598,1494 | 11,18761706 |
| 28 | 97662 | 0,003327804 | 325 | 8745,480415 | 97418,49355 | 26,700225 | 701,7471 | 101426,84 | 93410,14836 | 11,13929583 |
| 29 | 97337 | 0,003564934 | 347 | 7996,676302 | 88673,01314 | 26,153784 | 675,0469 | 92338,156 | 85007,86983 | 11,08873359 |
| 30 | 96990 | 0,003814826 | 370 | 7310,246493 | 80676,33683 | 25,584698 | 648,8931 | 84026,866 | 77325,80719 | 11,03606245 |
| 31 | 96620 | 0,004046781 | 391 | 6681,063461 | 73366,09034 | 24,804406 | 623,3084 | 76428,244 | 70303,93625 | 10,98119944 |
| 32 | 96229 | 0,004250278 | 409 | 6104,611614 | 66685,02688 | 23,803942 | 598,504 | 69482,974 | 63887,07989 | 10,92371327 |
| 33 | 95820 | 0,004445836 | 426 | 5576,757172 | 60580,41527 | 22,74619 | 574,7001 | 63136,429 | 58024,40156 | 10,86301831 |
| 34 | 95394 | 0,004654381 | 444 | 5093,544793 | 55003,65809 | 21,749814 | 551,9539 | 57338,199 | 52669,11673 | 10,7986992 |
| 35 | 94950 | 0,004865719 | 462 | 4651,227061 | 49910,1133 | 20,762902 | 530,2041 | 52041,926 | 47778,3009 | 10,73052608 |
| 36 | 94488 | 0,00514351 | 486 | 4246,417888 | 45258,88624 | 20,038068 | 509,4412 | 47205,161 | 43312,61137 | 10,65813291 |
| 37 | 94002 | 0,005499883 | 517 | 3875,758159 | 41012,46835 | 19,556162 | 489,4031 | 42788,858 | 39236,0792 | 10,58179243 |
| 38 | 93485 | 0,005947478 | 556 | 3536,185269 | 37136,71019 | 19,294848 | 469,8469 | 38757,462 | 35515,95861 | 10,50191304 |
| 39 | 92929 | 0,006488825 | 603 | 3224,91182 | 33600,52492 | 19,198062 | 450,5521 | 35078,61 | 32122,44034 | 10,4190523 |
| 40 | 92326 | 0,007083595 | 654 | 2939,436635 | 30375,6131 | 19,102549 | 431,354 | 31722,855 | 29028,37131 | 10,33382137 |
| 41 | 91672 | 0,00770137 | 706 | 2677,628309 | 27436,17647 | 18,918722 | 412,2515 | 28663,423 | 26208,93016 | 10,24644697 |
| 42 | 90966 | 0,008310797 | 756 | 2437,621011 | 24758,54816 | 18,585848 | 393,3327 | 25875,791 | 23641,3052 | 10,15684885 |
| 43 | 90210 | 0,008879282 | 801 | 2217,763703 | 22320,92715 | 18,066191 | 374,7469 | 23337,402 | 21304,45212 | 10,06461018 |
| 44 | 89409 | 0,009428581 | 843 | 2016,579408 | 20103,16345 | 17,443562 | 356,6807 | 21027,429 | 19178,89788 | 9,968942143 |
| 45 | 88566 | 0,009969966 | 883 | 1832,62929 | 18086,58404 | 16,762616 | 339,2371 | 18926,539 | 17246,62895 | 9,869199483 |
| 46 | 87683 | 0,010572175 | 927 | 1664,548659 | 16253,95475 | 16,144862 | 322,4745 | 17016,873 | 15491,03661 | 9,76478198 |
| 47 | 86756 | 0,011261469 | 977 | 1510,963999 | 14589,40609 | 15,61071 | 306,3297 | 15281,931 | 13896,88092 | 9,655694043 |
| 48 | 85779 | 0,012077548 | 1036 | 1370,594794 | 13078,44209 | 15,186628 | 290,719 | 13706,631 | 12450,25281 | 9,542165305 |
| 49 | 84743 | 0,013027625 | 1104 | 1242,239788 | 11707,8473 | 14,847187 | 275,5323 | 12277,207 | 11138,48739 | 9,42478852 |
| 50 | 83639 | 0,014084339 | 1178 | 1124,822344 | 10465,60751 | 14,534292 | 260,6851 | 10981,151 | 9950,063933 | 9,304231523 |
| 51 | 82461 | 0,015219316 | 1255 | 1017,412812 | 9340,785164 | 14,205804 | 246,1508 | 9807,0994 | 8874,470959 | 9,18091954 |
| 52 | 81206 | 0,016365786 | 1329 | 919,2004449 | 8323,372352 | 13,801319 | 231,945 | 8744,6726 | 7902,072148 | 9,055013407 |
| 53 | 79877 | 0,017539467 | 1401 | 829,5018416 | 7404,171907 | 13,347725 | 218,1437 | 7784,3603 | 7023,983563 | 8,926046377 |
| 54 | 78476 | 0,018719099 | 1469 | 747,6631389 | 6574,670066 | 12,839982 | 204,796 | 6917,349 | 6231,991127 | 8,793626064 |
| 55 | 77007 | 0,01997221 | 1538 | 673,0895034 | 5827,006927 | 12,333106 | 191,956 | 6135,5063 | 5518,507571 | 8,657105626 |
| 56 | 75469 | 0,021359764 | 1612 | 605,1802003 | 5153,917423 | 11,85918 | 179,6229 | 5431,2917 | 4876,543165 | 8,516335169 |
| 57 | 73857 | 0,022936215 | 1694 | 543,3520131 | 4548,737223 | 11,43343 | 167,7637 | 4797,7736 | 4299,700884 | 8,371621184 |
| 58 | 72163 | 0,024694095 | 1782 | 487,0546557 | 4005,38521 | 11,034288 | 156,3303 | 4228,6186 | 3782,151826 | 8,223687348 |
| 59 | 70381 | 0,026654921 | 1876 | 435,8048455 | 3518,330554 | 10,657196 | 145,296 | 3718,0744 | 3318,586667 | 8,073179063 |
| 60 | 68505 | 0,028713233 | 1967 | 389,1637631 | 3082,525709 | 10,251513 | 134,6388 | 3260,8924 | 2904,158984 | 7,920896037 |
| 61 | 66538 | 0,030794433 | 2049 | 346,7794619 | 2693,361946 | 9,7971349 | 124,3873 | 2852,3025 | 2534,421359 | 7,76678622 |
| 62 | 64489 | 0,032966863 | 2126 | 308,3491604 | 2346,582484 | 9,3259673 | 114,5902 | 2487,9092 | 2205,255785 | 7,610147148 |
| 63 | 62363 | 0,035229222 | 2197 | 273,5631707 | 2038,233323 | 8,8416677 | 105,2642 | 2163,6164 | 1912,850203 | 7,450686137 |
| 64 | 60166 | 0,03749626 | 2256 | 242,1337182 | 1764,670153 | 8,3294577 | 96,42253 | 1875,6481 | 1653,692198 | 7,287998406 |
| 65 | 57910 | 0,040269384 | 2332 | 213,8115682 | 1522,536434 | 7,8991377 | 88,09308 | 1620,5334 | 1424,539466 | 7,120926372 |
| 66 | 55578 | 0,043092591 | 2395 | 188,2582643 | 1308,724866 | 7,4426939 | 80,19394 | 1395,0099 | 1222,439828 | 6,951752535 |
| 67 | 53183 | 0,046161367 | 2455 | 165,2713101 | 1120,466602 | 6,9992199 | 72,75124 | 1196,216 | 1044,717251 | 6,779559024 |
| 68 | 50728 | 0,049459864 | 2509 | 144,6258353 | 955,1952918 | 6,5625451 | 65,75203 | 1021,4821 | 888,9084507 | 6,604596544 |
| 69 | 48219 | 0,053028889 | 2557 | 126,1217074 | 810,5694566 | 6,1358661 | 59,18948 | 868,37524 | 752,763674 | 6,426882994 |
| 70 | 45662 | 0,056896325 | 2598 | 109,5721224 | 684,4477491 | 5,7194964 | 53,05361 | 734,66831 | 634,227193 | 6,246550074 |
| 71 | 43064 | 0,061071893 | 2630 | 94,80538649 | 574,8756268 | 5,3118756 | 47,33412 | 618,3281 | 531,423158 | 6,063744351 |
| 72 | 40434 | 0,065563635 | 2651 | 81,66554318 | 480,0702403 | 4,9121925 | 42,02224 | 517,50028 | 442,6401997 | 5,878491976 |
| 73 | 37783 | 0,0704285 | 2661 | 70,01032418 | 398,4046971 | 4,5235982 | 37,11005 | 430,49276 | 366,3166318 | 5,690656368 |
| 74 | 35122 | 0,075650589 | 2657 | 59,70605696 | 328,3943729 | 4,1438517 | 32,58645 | 355,75965 | 301,0290968 | 5,500185235 |
| 75 | 32465 | 0,081256738 | 2638 | 50,63234731 | 268,688316 | 3,7745132 | 28,4426 | 291,89481 | 245,4818234 | 5,30665336 |
| 76 | 29827 | 0,087370503 | 2606 | 42,67718158 | 218,0559687 | 3,4208503 | 24,66809 | 237,61634 | 198,4955938 | 5,109427581 |
| 77 | 27221 | 0,093898093 | 2556 | 35,73252729 | 175,3787871 | 3,07818 | 21,24724 | 191,7562 | 159,0013787 | 4,908099156 |
| 78 | 24665 | 0,100952767 | 2490 | 29,70395515 | 139,6462598 | 2,7510977 | 18,16906 | 153,26057 | 126,031947 | 4,701268201 |
| 79 | 22175 | 0,10854566 | 2407 | 24,50023732 | 109,9423046 | 2,4398114 | 15,41796 | 121,17158 | 98,71302919 | 4,487397537 |
| 80 | 19768 | 0,116653177 | 2306 | 20,03747055 | 85,44206731 | 2,1444354 | 12,97815 | 94,625908 | 76,25822663 | 4,264114429 |
| 81 | 17462 | 0,125415187 | 2190 | 16,2385651 | 65,40459675 | 1,8684061 | 10,83371 | 72,847272 | 57,96192108 | 4,027732522 |
| 82 | 15272 | 0,134821896 | 2059 | 13,02936001 | 49,16603165 | 1,6115991 | 8,965305 | 55,137822 | 43,19424165 | 3,773480171 |
| 83 | 13213 | 0,144857337 | 1914 | 10,34194219 | 36,13667164 | 1,3744094 | 7,353706 | 40,876728 | 31,3966148 | 3,494186195 |
| 84 | 11299 | 0,155677494 | 1759 | 8,113610993 | 25,79472944 | 1,1588134 | 5,979297 | 29,513468 | 22,07599107 | 3,179192282 |
| 85 | 9540 | 0,167180294 | 1594,9 | 6,284866394 | 17,68111845 | 0,9639503 | 4,820483 | 20,561682 | 14,80055469 | 2,813284697 |
| 86 | 7945,1 | 0,239053001 | 1899,3 | 4,801982189 | 11,39625206 | 1,0531452 | 3,856533 | 13,597161 | 9,195343554 | 2,373239135 |
| 87 | 6045,8 | 0,341625591 | 2065,4 | 3,352343059 | 6,594269868 | 1,0506846 | 2,803388 | 8,1307604 | 5,0577793 | 1,967062962 |
| 88 | 3980,4 | 0,488066526 | 1942,7 | 2,024859522 | 3,241926809 | 0,9066662 | 1,752703 | 4,1699874 | 2,313866194 | 1,601062579 |
| 89 | 2037,7 | 0,695048339 | 1416,3 | 0,951003092 | 1,217067286 | 0,6064157 | 0,846037 | 1,6529437 | 0,78119087 | 1,279772166 |
| 90 | 621,4 | 0,981670422 | 610,01 | 0,266064195 | 0,266064195 | 0,2396214 | 0,239621 | 0,3880103 | 0,144118106 | 1 |
| Формула | lx*(1+i)-x | dx*(1+i)-x+1 | ||||||||
Таблица смертности – числовая модель процесса вымирания по возрастам некоторой абстрактной совокупности людей.
Прежде чем начать непосредственное описание методов расчета страховых аннуитетов и нетто-тарифов, необходимо сформулировать обще принципы определения нетто-премий в личном страховании.
В страховании жизни, как и в любом из видов страхования должно соблюдаться условие превышения страховых премий над страховыми выплатами (Е(Р)+I>=E(S)), где I – доход от инвестиций временно свободных средств. Величина страховых выплат является случайной величиной, и нельзя заранее предсказать точную сумму страховых выплат. За счет большого числа застрахованных, статистические данные однородны и обладают должной степенью надежности. Поэтому, вероятность отклонения реальных величин от их математического ожидания ничтожно мала. Вследствие этого, в актуарных расчетах принято использовать вероятную (ожидаемую) стоимость выплат. Тоже происходит и суммами нетто-премий. Их величина зависит от случайной величины S, а, следовательно, является величиной случайной.
К моменту осуществления выплат страховщик должен обладать фондом, равным вероятной стоимости выплат. Он определяет для себя будущую стоимость выплат и размер требуемого страхового фонда. Так как страховщик инвестирует свободные средства, то они ему приносят доход, который изменяется в зависимости от нормы доходности r, темпа инфляции (h), и ставки налогов (g). Тогда дисконтирование происходит по скорректированной ставке i=r(1-g)+h/100. Страховая премия выплачивается в момент заключения договора, то есть в современный момент времени, а страховые выплаты спустя определенное время. Поэтому, для их сравнения необходимо дисконтировать страховые выплаты, приводя их стоимость к сегодняшнему дню.
В страховании жизни нетто-премии иногда уплачиваются не одной суммой, а серией платежей, в различные периоды времени (в рассрочку). Для их учета страховщику приходится как нетто-премии, так и страховые выплаты приводить к одному моменту времени, иначе, при незапланированном прекращении договора, страховщик недополучит часть причитающихся ему премий.
Вышесказанное можно представить в виде неравенств, которые показывают основные принципы расчета тарифных ставок:
1. E+I>S – Нетто-премия с учетом дохода, от инвестиций должна превышать страховую выплату.
Если данное равенство не будет соблюдаться, то страховщик обанкротится.
2. E+I>Sp – Сумма выплат – величина случайная, так как неизвестно по каким договорам приходится возмещать ущерб. Поэтому в актуарных расчетах применяют ее наиболее вероятное значение (Sp).
3. E>Sp-I – Современная вероятная стоимость выплат (разница между суммой выплат и накопленных доходов) не должна превышать стоимость единовременной нетто-премии.
4. Ep-IE>Sp-I – Сравнение вероятной стоимости выплат происходит не с реальными суммами нетто-премий, а с их наиболее вероятным значением (математическим ожиданием). Современная вероятная стоимость нетто-премий, уплаченных в рассрочку, должна быть меньше, чем современная стоимость выплат.
Получается, что нетто-премии – доходы страховой компании, а страховые выплаты – ее расходы, причем и те и другие носят случайный характер. Так как в страховании жизни затронуты значительные периоды времени, в рамках которых изменяется стоимость денег пропорционально ставке i, то расчетные данные необходимо приводить к одному моменту времени.
Принцип финансовой эквивалентности (P=Sq) в страховании жизни несколько видоизменен. Пусть P – размер премии, qn – вероятность страхового события (смерть застрахованного через n лет после начала страхования). Если страховое событие произойдет на первом году страхования, то страховщик получит сумму Р, если на втором году – 2Р, и т.д. Математическое ожидание такого ряда премий составит: Pq1+2Pq2+3Pq3+…+nPqn. Однако, премия выплачивается в разные моменты времени. С учетом этого фактора данную величину необходимо привести к одному моменту времени (к начальному): E(P)=P(q1+(1+v)q2+(1+v+v2)q3+…+(1+v+…+vn-1)qn), где v=(1+i)-1-дисконтный множитель. Е(Р) – дисконтированное математическое ожидание страховых премий.
Теперь рассмотрим совокупность страховых выплат. Допустим, они выплачиваются в конце года, в котором имел место страховой случай. Тогда математическое ожидание выплаты в первом году составит Sq1, во втором году -Sq2, и т.д. С учетом фактора времени математическое ожидание страховых выплат выглядит так: E(S)=S(vq1+v2q2+…+vnqn)/
Как известно, E(S)=E(Р). Подставляя известные значения в данное равенство можно определить размер нетто-премии.
Зная основные принциы формирования нетто-премии в страховании жизни можно перейти к рассмотрению методов ее расчета. Итак, основной показатель таблицы смертности – число людей lx в возрасте х лет, оставшихся в живых из первоначальной совокупности l0 (обычно равной 100000 человек). Величины lx (кроме l0) определяют расчетным путем на основе заданных вероятностей смерти (qx)в возрасте х лет, или на основе количества умерших (dx). Указанные вероятности получают на основе данных статистики населения с последующим усреднением и сглаживанием.
Показатели таблицы смертности связаны следующими соотношениями:
- lx+1=lx-dx;
- dx=lx*qx;
- qx=1-px=1-lx+1/lx=dx/lx .
Для определения страховых тарифов необходимо знать страховые вероятности в страховании жизни и действия над ними:
1. npx=lx+n/lx– вероятность прожить n лет лицо, дожившим до возраста х лет.
2. px=1-qx=1-dx/lx=lx+1/lx– вероятность человеком, дожившим до х лет, прожить еще 1год.
3. nqx=1-npx=(lx-lx+n)/lx – вероятность умереть в интервале возрастов от x лет до n лет.
4. mqx=mpx*qx+m=(lx+m/lx)*(dx+m/lx+m)=dx+m/lx - вероятность дожить до возраста х лет и умереть в возрасте x+m лет в течении 1 года.
5. m/nqx=mpx*nqx+m=(lx+m/lx)*(lx+m-lx+m+n)/lx+m=(lx+m-lx+m+n)/ lx– вероятность дожить до x+m лет и умереть в возрасте от x+m лет до x+m+n лет.
Для упрощения расчетов и сокращения записи формул в таблицах смертности используются коммутационные функции. Их смысл сложно интерпретировать, поэтому они должны восприниматься как чисто технические вспомогательные средства. Их можно разделить на две группы. В основу первых положены числа доживающих до определенного возраста, вторых – числа умерших.
1. Dx=lx*vx
2. , где w-предельный возраст, учитываемый в таблице смертности.
- Nx=Nx+1+Dx; Nw=Dw
- (Nx+1-Nx+2)+(Nx+2-Nx+3)+…+Nx+k-Nx+k+1=Nx+1-Nx+k+1
3. Cx=dx*vx+1; Cx=dx*vx+1=(lx-lx+1)*vx+1=lx*vx*v-lx+1*vx+1=Dx*v-Dx+1
4. ;
Страхование на дожитие.
Страхователь и страховщик договариваются между собой о том, что второй выплатит первому страховую сумму S, если он доживет до возраста n. В обмен на данные условия страхователь предлагает заплатить страховщику нетто-премию, которая равна произведению страхового тарифа и размера выплаты (nEx*S). Нетто-премия может уплачиваться единовременно, а может в рассрочку, что ведет к различной методике расчета:
1. Нетто-премия уплачивается единовременно. В этом случае страхователь обязательно ее заплатит, иначе договор не будет заключен. Страховая выплата зависит от того, доживет ли страхуемый до n лет или нет. Поэтому, при ее расчете применяется математическое ожидание от суммы выплаты (S*npx). Страховая выплата произойдет только через n лет после заключения договора, поэтому ее необходимо привести к моменту уплаты нетто-премии (S*npx*vn). Используя принцип финансовой эквивалентности (обязательства должны быть равны), получается:
- nEx*S = S*npx*vn
- nEx= npx*vn= (lx+n/lx)* vn
- nEx=(lx+n*vx+n/lx*vx+n)* vn=Dx+n/Dx
2. Нетто-премия уплачивается в рассрочку. Здесь нетто-премия представляет собой поток платежей от страхователя страховщику, при этом все платежи составляющие нетто-премию в данном виде страхования – суммы фактические, а не вероятные, так как если человек умрет раньше времени, то он не получит страховую сумму, а у страховщика останется часть нетто-премий, которые он никому не должен. Пусть, страховые премии уплачиваются в течении t лет, в начале каждого года. Тогда P1*S – премия уплаченная в первом году, Р2*S – премия уплаченная во втором году и т.д.
- (P1+P2*v+…+Pt*vt-1)*S = S*npx*vn
- Если платежи одинаковы, то P(1+v+v2+…+vt-1)=npx*vnили
Страхование жизни.
Этот вид страхования называют также страхованием на случай смерти. Страховая сумма, равная S, выплачивается в случае смерти застрахованного. Страховой договор заключается страхователем в x лет на срок n лет. Здесь также следует рассмотреть два случая:
1. Нетто-премия уплачивается единовременно. Тогда обязательства страхователя равны произведению страхового тарифа и страховой суммы (S*nAx). Нетто-премия – основное условие заключение договора, поэтому ее величина для страховщика реальная, а не вероятная. Если выплаты страховых сумм происходят в конце года, и страхователь умрет в 1-ый год, то страховая сумма будет равна S*qx*v (qx – вероятность умереть в возрасте х лет); если во второй год, то страховщик должен будет заплатить S*2qx*v2=S*v2*dx+1/lx;
- если умрет в третий год – страховая выплата = S*v3*dx+2/lx и так далее.
- В силу финансовой эквивалентности:
S*nAx=S*dx/lx*v+ S*dx+1/lx*v2+S*dx+2/lx*v3+…+S*dx+n-1/lx*vn
- Умножим и разделим данное выражение на vx,тогда:
nAx=(dx/Dx)*vx+1+(dx+1/Dx)*vx+2+(dx+2/Dx)*vx+3+…+(dx+n-1/Dx)*vx+n=1/Dx *(Cx+Cx+1+…+Cx+n-1)
Mx=Cx+Cx+1+…+Cx+n-1+Cx+n+Cx+n+1+…+Cw
Mx+n= Cx+n+Cx+n+1+…+Cw
Mx-Mx+n= Cx+Cx+1+…+Cx+n-1
nAx= 1/Dx *(Mx-Mx+n)
- Если страхование пожизненное, то nAx= Mx/Dx
2. Нетто-премия вносится в рассрочку. Пусть рассрочка осуществляется посредством равных платежей (P) пренумерандо (в начале года) в течении t лет. В данном случае нетто-премия представляет собой поток платежей, ограниченный периодом t. При этом каждый член этого потока, является случайной величиной, так как при наступлении страхового случая платежи прекратятся, а страховщик должен будет уплатить всю страховую сумму страхователю. Наступление каждого последующего платежа не определено, так как неизвестно наступит ли страховой случай. Страховщик должен учитывать, что если он произойдет, то он потеряет не только страховую сумму, но и премии.
- Исходя из принципа финансовой эквивалентности можно записать следующие выражение: S*(P+P*px*v+P*2px*v2+P*3px*v3+…+P*t-1pxvt-1) = S*dx/lx*v+ S*dx+1/lx*v2+S*dx+2/lx*v3+…+S*dx+n-1/lx*vn
- P*(1+lx+1/lx*v+lx+2/lx*v2+lx+3/lx*v3+…+lx+t-1/lx*vt-1)= (Mx-Mx+n)/Dx
- P*( 1+lx+1/lx*v+lx+2/lx*v2+lx+3/lx*v3+…+lx+t-1/lx*vt-1)* (vx/vx)= (Mx-Mx+n)/Dx
-
-
Страховые выплаты, а иногда и страховые премии представляют собой поток платежей, что в финансовой математике называется аннуитетом (страховой рентой). Стоимость страхового аннуитета, по сути, является отправным моментом в актуарной математике. Как известно, платежи могут вносится в начале года – пренумерандо, и в конце года - постнумерандо. В зависимости от этого различаются и виды аннуитетов. Кроме этого в страховании ренты делятся в зависимости от интервала времени, в котором производятся платежи. Аннуитет уже применялся в приведенных выше расчетах. Далее он будет рассмотрен более подробно, так как широко используется в пенсионном и других видах страхования, о которых речь пойдет ниже.
Виды страховых аннуитетов.
| Пояснение | Формула | |||||||
| Постнумерандо. | ||||||||
| Аннуитет пожизненный, немедленный – лицу, начиная с возраста х лет пожизненно в конце года выплачивается по 1 рублю. | ||||||||
| Аннуитет отложенный на n лет, пожизненный – уплачивается пожизненно лицу в возрасте x+n лет по одному рублю в конце каждого года. | ||||||||
| Аннуитет немедленный, ограниченный – выплачивается лицу в возрасте x лет в течение t лет, по 1 рублю, в конце каждого года. | ||||||||
| Аннуитет отложенный на n лет, ограниченный – лицу, в конце каждого года выплачивается по 1 рублю, начиная с возраста n лет, до возраста t лет. | ||||||||
| Пренумерандо. | ||||||||
| Аннуитет пожизненный, немедленный | Выплаты производятся в начале года. | |||||||
| Аннуитет отложенный на n лет, пожизненный | ||||||||
| Аннуитет немедленный, ограниченный | ||||||||
| Аннуитет отложенный на n лет, ограниченный | ||||||||
| Соотношения | ||||||||
| Рента уплачиваемая k раз в год. | ||||||||
| Для ограниченной ренты | ||||||||
| Для пожизненной ренты. | ||||||||
Пенсионное страхование.
С экономической точки зрения обеспечение пенсиями по старости на базе негосударственных пенсионных фондов – это долгосрочный инвестиционный процесс, на первом этапе которого осуществляются вложения (пенсионные взносы) и последовательное наращение вложенных сумм за счет инвестиций свободных денежных средств, на втором – получение отдачи от накоплений в виде периодических пенсий.
Пенсионное страхование делится на два вида:
Похожие работы
... (застрахованного) в результате страхового случая, т. е. фактически происшедшего страхового события [11, с. 49]. В зарубежной страховой практике широко применяется страхование экономических рисков: коммерческих, технических, правовых, политических и рисков в финансово-кредитной сфере. Риск является объективной предпосылкой возникновения страховых событий; если нет риска — нет и потребности в ...
... , точность тарифа обеспечивается меньшим значением коэффициента и, в конечном итоге, рисковой надбавки (Tр). 3. Рассчитывается тарифная нетто-ставка на 100 руб. страховой суммы или в процентах. Особенности актуарных расчетов по добровольному медицинскому страхованию. Добровольное медицинское страхование (ДМС) в плане актуарных расчетов отличается от других рисковых видов страхования тем, что в ...
... экстраполяции). Располагая даже простейшей таблицей смертности, можно рассчитать ряд показателей, характеризующих смертность и доживаемость среди изучаемого населения, которые позволят рассчитать тарифы по страхованию жизни. Например, при страховании на дожитие страховщик обязуется выплатить страховую сумму застрахованному лицу, если тот доживет до конца срока страхования. Для определения размера ...
... страхового сообщества; эффективная деятельность профессиональных ассоциаций страховщиков, страховых посредников и обществ по защите прав страхователей. Отдельные проблемы развития страхового рынка находятся в стадии решения. Например, в интересах повышения прозрачности своей деятельности для зарубежных инвесторов некоторые страховые организации уже приступили к внедрению международных ...


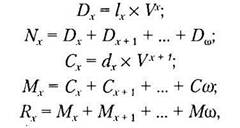
0 комментариев