Теорема Гаусса, уравнение Пуассона

10. Теорема Гаусса, уравнение Пуассона.

 Рассмотрим систему зарядов:

Ф_Е = оòЕ_ndS, где E_n = E₁ + E₂ + E₃ + + … = SE_ni, i = 1 ¸ N.

Ф_Е = oòSE_nidS = Sò E_nidS = S(q_i/e₀) = = (Sq_i)/e₀, i = 1 ¸ N.

Теорема (Остроградского -) Гаусса: Поток вектора Е (Ф_Е) через замкнутую поверхность равен алгебраической сумме зарядов, охватываемых данной поверхностью, поделенной на e₀.

] заряд распределен внутри некого объема с некой объемной плотностью r, тогда q = _VòrdV. Ф_Е = oòEdS = /E и S – вектора/ = 1/(e₀e)*_VòrdV, где V – объем, в котором находятся заряды, а не весь объем области.

e - определяет св-ва среды, в которой находятся заряды (e = 1 в вакууме и/или в воздухе).

Индукция:

Д - прописное.

Д - вектор индукции, отличающийся от Е на некую константу, зависящую от среды.

Д = e₀eE /Д и Е – вектора/;

Ф = о_SòДdS = /Д и S – вектора/ = =_VòrdV – ур-е Максвелла.

11. Бесконечная заряженная плоскость:

Она заряжена с постоянной поверхностной плотностью заряда g.

n

E

E E

E E

Выбирается некая поверхность, окруженную зарядом. Определяется вектор Е и Ф_Е и точка на основании цилиндрической поверхности. oò E_ndS = (åq)/e₀.

Данное направление Е выбирается, т.к. плоскость бесконечна и нет других преимущественных направлений. В любой точке поверхности Е постоянно и a для любой точки одинакова.

oò E_ndS = _Sб.п.ò E_ndS + _Sосн.ò E_ndS = = /a_б.п. = 90⁰/ = _Sосн.ò E_ndS = E _Sоснò dS = = E 2S = /по т-ме Гаусса/ = (1/e₀)^.g^.S.

Е = g/(2e₀).

12. Поле двух разноименно заряженных плоскостей:

Еå=g/e0

+g

-g

Еå=0

Еå=0

Е-

Е-

Е-

Е+

Е+

Е+

Часть векторов Е одинакова по величине, то E_å = g/e₀.

13. Поле бесконечного заряженного цилиндра:

E=0

l

t

R

Бесконечный цилиндр R с линейной плотностью заряда t (заряд на единицу длинны).

r

q – заряд на цилиндре.

q = l^.t или q = g^.2pR^.l

E = t/(2pe₀r)

E

E_r

~1/r

r

_R

R

r

E=0

l

r

Бесконечный заряженный цилиндр с объемной плотностью r.

 n

E

Ф_Е = E _Sб.п.òdS = E2prl

q = rV_Ц = rpR²l = 1/e₀ rpR²l

E = (rR²)/(e₀2r).

 

r

l

R

q = rpr²l

Ф = E2prl = (1/e₀) rpr²l

E = (rr)/(2e₀)

Если есть e₁ и e₂, то e_0*e₁₍₂₎

E

1

2

3

r

1 - e₁ > e₂;

2 - e₁ = e₂;

3 - e₁ < e₂.

14. Поле бесконечного заряженного шара (сферы):

Заряд с поверхностной плотностью g распределен по сфере радиуса R:

g

Е

|E| - const;

Ф_Е = _SoòE_ndS = E oòdS = E 4pr² = = (1/e₀) g4pR²

q = g 4pR²

E_наружн = (gR²)/(e₀r²) = q/(4pe₀r²)

E_внутр= 0

E

E_r

~1/r

r

R

Заряд с поверхностной плотностью g распределен по шару радиуса R:

Ф = Е 4pr² = (r/e₀) 4/3 pR³

q_наружн = rV = r 4/3 pR³

E_наружн = (gR²)/(e₀r²) = q/(4pe₀r²)

E_внутр = (rr)/(3e₀e₁)

E

1

E_r

2

r

_R

Шар с r(r):

E_наружн = q/(4pe₀e₂r²)

dq = r(r’) 4pr’ dr’

r’ – толщина внутреннего слоя;

q = ₀ò^Rr(r’) 4pr’² dr’

E_наружн = (4p ₀ò^Rr(r’) 4pr’² dr’)/ /(4pe₀e₂r²); _r

E_внутр = (4p ₀òr(r’) 4pr’² dr’)/ /(4pe₀e₁r²);

Шар с полостью:

E_наружн = (4p _R1ò^R2r(r’) 4pr’² dr’)/ /(4pe₀e₂r²); _r

E_внутр = (4p _R1òr(r’) 4pr’² dr’)/ /(4pe₀e₁r²).

 

15. Потенциал (j):

]$ поле, создаваемое неподвижным точечным зарядом q. ]$ точечный заряд q’, на который действует сила:

F = 1/(4pe₀)_*(qq’)/r²

Работа, совершаемая над зарядом q’ при перемещении его из одной точки в другую, не зависит от пути

A₁₂ = ₁ò² F(r)dr = (qq’)/(4pe₀)_r1ò^r2dr/r².

Иначе ее можно представить, как убыль потенциальной энергии:

A₁₂ = W_p1 – W_p2.

При сопоставлении формул получаем, что W_p = 1/(4pe₀)_*(qq’)/r.

Для исследования поля воспользуемся двумя пробными зарядами q_ПР’ и q_ПР’’. Очевидно, что в одной и той же точке заряды будут обладать разной энергией W_p’ и W_p’’, но соотношение W_p/q_ПР будет одинаковым.

j = W_p/q_ПР = 1/(4pe₀)_*q/r называется потенциалом поля в данной точке и, как напряженность, используется для описания электрического поля.

]$ поле, создаваемое системой из N точечных зарядов. Работа, совершаемая силами этого поля над зарядом q’, будет равна алгебраической сумме работ, совершаемых каждым из q_N над q’ в отдельности:

A = _{i = 1}å^NAi, где Ai = = 1/(4pe₀)_*(q_iq’/r_i1 - q_iq’/r_i2), где r_i1 - расстояние от заряда q_i до начального положения заряда q’, а  r_i2 – расстояние от q_i до конечного положения заряда q’.

Следовательно Wp заряда q’ в поле системы зарядов равна:

Wp = 1/(4pe₀)_{*i = 1}å^N(q_iq’)/r_i , то

j = 1/(4pe₀)_{*i = 1}å^N(qi/r_i), следовательно потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.

Заряд q, находящийся в точке с потенциалом j обладает энергией

Wp = qj, то работа сил поля

A₁₂ = Wp₁ –Wp₂ = q(j₁ - j₂).

Если заряд из точки с потенциалом j удалять в бесконечность, то A¥ = qj, то j численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки на бесконечность.

16. Связь между напряженностью и потенциалом:

Электрическое поле можно описать с помощью векторной величины Е и скалярной величины j.

Для заряженной величины, находящейся в электрическом поле:

F = qE, Wp = qj.

Можно написать, что

E = - ¶j/¶x - ¶j/¶y - ¶j/¶z, т.е. при проекции на оси:

E_x = -¶j/¶x, E_y = -¶j/¶y, E_Z = -¶j/¶z, аналогично проекция вектора Е на произвольное направление l: Е_l = = -¶j/¶l, т.е. скорости убывания потенциала при перемещении вдоль направления l.

j = 1/(4pe₀)_*q/r = /в трехмерном пространстве/ = 1/(4pe₀)_*q/Ö(x²+y²+z²).

Частные производные этих функций равны:

¶j/¶x = -q/(4pe₀)_*x/r³;

¶j/¶y = -q/(4pe₀)_*y/r³;

¶j/¶z = -q/(4pe₀)_*z/r³.

При подстановке получаем:

E = 1/(4pe₀)_*q/r².

Работа, по перемещению q из точки 1 в точку 2, может быть вычислена, как A₁₂ = ₁ò²qEdl или A₁₂ = q(j1 - j2), приравняв их, получим j1 - j2 = ₁ò²Edl. При обходе по замкнутому контуру j1 = j2, то получим: oò Edl = 0.

17. Эквипотенциальные поверхности:

Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной. Ее уравнение имеет вид j(x, y, z) = const.

При перемещении по эквипотенциальной поверхности на отрезок dl, dj = 0. Следовательно, касательная к поверхности, составляющая вектор Е, равна 0, т.е. вектор Е направлен по нормали к эквипотенциальной поверхности. Т.е. линии напряженности в каждой точке перпендикулярны к эквипотенциальным поверхностям.

Эквипотенциальную поверхность можно провести через любую точку поля и их можно построить бесконечное множество. Их проводят таким образом, чтобы разность потенциалов для двух соседних поверхностей была одинаковой (Dj = const). Тогда по густоте эквипотенциальных поверхностей можно судить о величине напряженности поля.

В соответствии с характером зависимости Е от r, эквипотенциальные поверхности при приближении к заряду становятся гуще. Для однородного поля эквипотенциальные поверхности представляют собой систему равноотстоящих друг от друга плоскостей, перпендикулярных к направлению поля.

18. Проводники в электрическом поле:

Проводники состоят из связанных зарядов равномерно распределенных по объему проводника. Электроны проводника находятся в тепловом хаотическом движении.

]$ поле с проводником:

₍₎ 1

- + Е

 - +

- + Е

- +() 2

-  + Е

- +

-- + Е

- +

+ Е

- +

Напряженность внутри проводника равна 0, т.к. внутри проводника складывается некая суперпозиция напряженностей.

Если j1 - j2 = 0, то поверхность проводника эквипотенциальна, а линии напряженности всегда перпендикулярны эквипотенциальной поверхности.

Возьмем произвольную точку плоскости проводника.

t

j

Возьмем касательную к элементу поверхности t.

dj/dt = -Et, (где dj/dt = 0) вектор Е перпендикулярен плоскости в данной точке.

 q

Е = 0

E ~ g

(g - поверхностная плотность)

Заряд распределен по поверхности, Е = 0, распределение неравномерно, максимальную плотность заряд имеет в местах максимальной кривизны.

Обозначим «степень кривизны» за С, то С = 1/R.

E ~ g ~ C ~ 1/R.

19. Электроемкость, конденсаторы:

Электроемкость – коэффициент пропорциональности между зарядом проводника и потенциалом, который заряд приобретает. Зависит от формы проводника и окружающих его тел.

С = q/j.

Электроемкости уединенных проводников (на него ни что не влияет):

Сфера: q

j = 1/(4pe₀)_*q/R

C = q/j = 4pe₀R

R j

Если поместить около сферы другой проводник, то С = Dq/Dj.

-Dq

_R

Dq

E₊

 X E-

+Dq

l

_R

Dj - разность потенциалов, возникшая между проводниками.

Если l>>R, то заряд по поверхности каждой сферы распределяется равномерно.

Dj = j1 - j2

j1 - j2 = _Rò^l-R Edx

E = E₊ + E- = k_*Dq/x² + k_*Dq/(l-x)²

Конденсаторы:

С = 4pe₀R

Плоский:

 q+ q- C = Dq/(j1 - j2) =

= (Dqe₀S)/(Dqd) =

= e₀S/d

j1 - j2 = E_*d =

= gd/e = (Dqd)/(e₀S)

 j1 j2

Сферический:

R1

R2

+q

-q

j1 - j2 = _R1ò^R2E₊dr = = Dq/(4pe₀) _{* R1}ò^R2 (1/r²)dr = = Dq/(4pe₀)_*(1/R₁ – 1/R₂).

C = (4pe₀eR₁R₂)/(R₂-R₁).

20. Электрическое поле в диэлектриках:

При помещении в поле диэлектрика в поле происходит изменение. Сам диэлектрик реагирует на поле иначе, чем проводник.

Заряды, входящие в состав молекул диэлектрика, называются связанными. Они не могут покидать пределы молекулы, в которую они входят.

Заряды не входящие как в состав молекул диэлектрика, так и в сам диэлектрик называются сторонними.

Поле в диэлектрике является суперпозицией полей сторонних и связанных зарядов и называется микроскопическим (или истинным).

Е_МИКРО = Е_СТОР + Е_СВЯЗ

Микроскопическое поле в пределах диэлектрика непостоянно, поэтому

Е₀ = <Е_МИКРО> = <Е_СТОР> + <Е_СВЯЗ>

<Е_СВЯЗ> = E’

Макроскопическое поле:

E = E₀ + E’

При отсутствии диэлектрика макроскопическое поле равно

Е = Е₀ = <Е_СТОР>.

Если сторонние заряды неподвижны, то поле Е_МИКРО обладает теми же свойствами, как электростатическое поле в вакууме.

При определении суммарного действия всех электронов имеет значение и центр масс отрицательных зарядов.

®

q- l q+

® ®

r-                   r+

_®®

 r- = (_{i = 1}å^Nr_iq_i-)/( _{i = 1}å^Nq_i-)

_®

r+ = (_{j = 1}å^Nr_jq_j+)/( _{j = 1}å^Nq_j+)

Полярные и неполярные молекулы во внешнем поле приводят развороту диполя в направлении поля. Неполярные молекулы приобретают электрический момент. Они поляризуются, от чего возникает дипольный момент, направленный вдоль внешнего поля. Молекула ведет себя как упругий диполь.

21. Диполь в однородном и неоднородном электрических полях:

В однородном поле:

®

 ®

E

l +q

_Fk

_®

M a

_Fk^(X)-q

M = Fk_*l_*sina = q_*E_*l_*sina = = P_*E_*sina, где P – дипольный момент.

® ® ®

M = [P x E]

®

M – направлен «от нас»

dA = Mda = P_*E_*sina da

dA = dW _®®

W = -P E cosa = -(P E)*

* - cкалярное произведение.

В неоднородном поле:

®  ®

X

+q F+ Е

l

-q_DX

®

F-

DF = (F+) – (F-) = q_*DE = = q_*¶E/¶X_*l_*cosa = P_*¶E/¶X_*cosa = = /кроме вращающего момента на диполь действует сила, зависящая от угла a, если угол острый, то диполь «втягивается» внутрь поля/ = = ¶(PEcosa)/¶X = -¶W/¶X.

22. Поляризация диэлектриков:

®

Р – параметр, описывающий состояние диэлектрика в электрическом поле.

® ®

P = (_{i = 1}å^NPi)/DV

(-+)(-+) (-+)(-+)

(-+)(-+) (-+)(-+)

(-+)(-+) (-+)(-+)

(-+)(-+) (-+)(-+)

(-+)(-+) (-+)(-+) ®

(-+)(-+) (-+)(-+)  Е

(-+)(-+) (-+)(-+)

(-+)(-+) (-+)(-+)

(-+)(-+) (-+)(-+)

На поверхности возникают связанные заряды с плотностью g_СВЯЗ.

® ®

P = He₀E

H – коэффициент диэлектрической восприимчивости;

Е – результирующий вектор.

E

DS l

® n

P

n

d

-g +g

P_*DV – суммарный дипольный момент молекул внутри цилиндра.

DV = DS_*l_*cosa

P_*DV = P_*DS_*l_*cosa = q_*l

q = g_СВЯЗ*DS

P_*DS_*cosa_*l = g_СВЯЗ*DS_*l

P_*cosa = g_СВЯЗ

g_СВЯЗ = He₀E, где Е – результирующее поле в диэлектрике.

® ® ®

Е = Е₀ + Е’

Внешнее поле должно ослабляться:

® ® ® ® ®

Д = e₀Е + Р = e₀E + He₀E =

® ®

= (1 + H)e₀E = ee₀E.

23. Поле внутри плоской диэлектрической пластины:

+g₀  -g₀

 

Е₀

- +

- +

- +

g₀ – свободные перемещающиеся заряды, создающие Е₀ (вектор);

Число силовых линий уменьшается во столько раз, какое значение имеет e.

Е₀ = g₀/e₀

Е = Е₀ – Е’ = g₀/e₀ - g_СВЯЗ/e₀ = = 1/e₀(g₀ - g_СВЯЗ);

E = E₀ – HE ® E_*(1 +H) = E₀ ® E = E₀/(1+H) = E₀/e;

Д = e₀eE = e₀E, т.е. вектор индукции внутри не изменяется, плотность силовых линий остается постоянной.

E = 1/e_0*(g₀ - g_СВЯЗ) = E₀/e =g₀/(e₀e);

g_CВЯЗ = g_0*(e - 1)/e.

25. Сегнетоэлектрики:

Существуют группы веществ, которые могут обладать самопроизвольной поляризованностью в отсутствие внешнего поля. Подобные вещества получили название сегнетоэлектриков.

Впервые свойства сегнетоэлектриков было изучено Курчатовым.

Отличия сегнетоэлектриков от остальных диэлектриков:

1) Диэлектрическая проницаемость сегнетоэлектриков измеряется тысячами, а у диэлектриков – десятками.

2) Диэлектрическая проницаемость сегнетоэлектриков зависит от напряженности поля.

3) Сегнетоэлектрики обладают явлением гистерезиса (запаздывания):

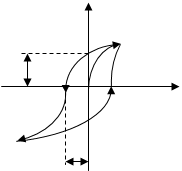P

1

Pr  2 3

E

 

 E_C

При изменении поля значение поляризованности Р и смещения D отстают от напряженности поля Е, в результате чего P и D зависят не только от текущего значения Е, но и от проедшествующего. Это явление называется гистерезисом.

На участке (2), при обращении Е в ноль, сохраняется остаточная поляризованность Pr. Она становится равной нулю только под действием противоположнонаправленного поля Е_С, называемой коэрцетивной силой.

Сегнетоэлектриками могут быть только кристаллические вещества с отсутствующим центром симметрии.

У каждого сегнетоэлектрика $ темпиратура, называемая точкой Кюри, при которой он утрачивает свои свойства и становиться обычным диэлектриком.

26. Поведение векторов напряженности и индукции на границе двух сред:

Et₁

e₁

®

® n1

En₁ a1

dh

Et₂

a2 ® ®

 En₂ n2

e2

Выделим на границе сред тонкую «шайюбу» толщиной dh ® 0 и площадью S. Подсчитаем поток индукции Д через выделенный объем.

Дn_2*S_*cos0^o + Дn_1*S_*cos180^o + Ф_БОК = 0, где Ф = 0, т.к. dh ® 0;

Дn_2*S - Дn_1*S = 0 ® Дn₂ = Дn₁ ® ® e₀e₂En₂ = e₀e₁En₁ ® En₂/En₁ = e₁/e₂.

Дn – неприрывна, а Еn терпит разрыв. ®

Рассмотрим циркуляцию вектора Е по контуру на границе раздела с dh ® 0:

®

®  E₁t

E₁

Et₂ l

Et₁

E₂

®

E₂t

E₁t l cos0^o + E₂t l cos180^o + + E_БОКdh cos90^o = 0;

Et₁ = Et₂; Дt₁/(e₀e₁) = Дt₂/(e₀e₂) ® ® Дt₁/ Дt₂  = e₁/e₂ (Е₁ и Д₁ сонаправленны, как и Е₂ и Д₂);

tga₁/tga₂ = (Et₁/ En₁)_*(En₂/Et₂) = = En₂/En₁ = e₁/e₂.

27. Энергия электрического плоля:

Плотность энергии – энергия, приходящаяся на единицу объема поля.

w = W/V – в однородном поле;

w = dW/dV - в неоднородном поле.

[w] = Дж/м³;

Определим w в поле плоского конденсатора:

W = CU²/2 = (e₀eSU²)/(2d), где U – разность потенциалов на обкладках конденсатора;

d – расстояние между обкладками;

V = S_*d;

w = W/V =(e₀eSU²)/(2d_*Sd) = = (e₀eU²)/(2d²);

U/d = E;

w = (e₀eE²)/2 = EД/2 = Д²/(2e₀e)

В сегнетоэлектриках w = 1/2 S петли гистерезиса.

Очевидно, что w характеризует поле в конкретной точке, как Е и Д.

W = _VòwdV – энергия поля.

Энергия взаимодействия двух точечных зарядов:

W = q_1*j₂ = (q₁q₂)/(4pe₀er) – энергия взаимодействия, она делится поровну между зарядами.

Энергия одного заряда:

W_i = 1/2 q_ij_i;

Энергия поля из N зарядов:

W = 1/2 _i=1å^Nq_ij_i, при этом i ³ 2.

28. Классическая теория электропроводности металлов:

Существует предположение, что электроны проводимости в металле ведут себя подобно молекулам идеального газа. В промежутках между соударениями они движуться совершенно свободно, пробегая в среднем некоторый путь l. Но в отличии от газа, электроны в металле сталкиваются приемущественно не сами с собой, а с ионами, образующими кристаллическую решетку металла.

Оценку средней скорости теплового движения электронов можно произвести по формуле:

<u> = Ö(8kT)/(pm), для комнатной темпиратуры <u> » 10⁵ м/с.

При включении поля на хаотическое тепловое движение, происходящее с <u>, накладывается упорядоченное движение электронов с <u>:

j = ne<u>, где j – плотность тока; для меди <u> » 10^-3 м/с.

Вызываемое полем изменение среднего значения кинетической энергии электронов.

<(u + u)²> = <u² + 2uu + u²> = = <u²> + 2<uu> + <u²> Û

Û <(u + u)²> = <u²> + <u²>, значит упорядоченное движение увеличивает кинетическую энергию в среднем на <Dek> = (m<u²>)/2.

29. Природа носителей зарядов металла:

В результате проведения ряда опытов /трамвайная линия/ было доказано, что заря в металлах переносится не атомами, а другими частицами, предположительно электронами. Если это так, то при резком торможении частицы должны продолжить свое движение и перенести некоторый заряд.

] проводник движется со скоростью v₀ и резко затормаживается с ускорением w. Продолжая двигаться по инерции, носители приобретут ускорение –w. Такое же ускорение можно создать, подействовав на проводник электрическим полем с E = -mw/e’, т.е. приложив к концам проводника разность потенциалов:

j1 - j2 = ₁ò²Edl = -₁ò²(mw)/e’dl = = -mwl/e’, где l – длина проводника. В этом случае по проводнику потечет ток I = (j1 - j2)/R.

Таким образом за время торможения прошел заряд

q = òdq = -_u0ò⁰ml/(e’R)du = = (m/e’)_*(lu₀/R), заряд положителен, если он переносится в направлении движения проводника.

Существование в металлах свободных электронов можно объяснить тем, что при образовании кристаллической решетки, от атомов отщепляются слабее всего связанные электроны.

30. Закон Видемана – Франца:

Известно, что металлы обладают как высокой электропроводностью, так и большой теплопроводностью. Видеман и Франц в 1853 году установили, что отношение коэффициента теплопроводности Н к коэффициенту электропроводности s для всех металлов примерно одинаковое и изменяется пропорционально абсолютной темпиратуре. Тот факт, что теплопроводность металлов значительно превышает теплопроводность диэлектриков говорит о том, что и теплопроводность в металлах осуществляется с помощью свободных электронов.

Рассматривая электроны как одноатомный газ получим:

H = 1/3 nmulC_V, где С_V = 3/2 (k/m), то H = 1/2 nkul.

Таким образом

H/s = (kmu²)/e² = 3(k/e)²T = = 2,23_*10^{¾ 8}_*T.

31. Постоянный электрический ток, его плотность и ЭДС:

Если через некоторую поверхность переносится суммарный заряд, отличный от нуля, то говорят, что через эту поверхность течет электрический ток. Ток может течь в тветдых телах (металлы, полупроводники), в жидкостях (электролиты) и газах (называется газовым разрядом).

Для протекания тока необходимо наличие заряженных частиц, которые могут перемещаться в пределах всего тела, называемых носителями тока. Ими могут быть электроны, ионы или макроскопические частицы, несущие на себе избыточный заряд.

Ток возникает при условии, что внутри тела $ эл. поле. Носители заряда принимают участие в молекулярном тепловом движении и движуться с некой v и в отсутствии заряда, но т.к. движение хаотическое, то ток = 0. При появлении поля на хаотическое v накладывается упорядоченное u. Т.о. u = v + u, но т.к. <v> = 0, то <u> = <u>.

Значит эл. ток – упорядоченное движение электрических зарядов.

Эл. ток колличественно характеризует величина, равная величине заряда, переносимого через рассматриваемую поверхность за единицу времени, и называемая силой тока, т.е. поток заряда через поверхность.

I = dq/dt, где dt – время, за которое через поверхность переносится заряд dq.

Перенос “-“ заряда в одном направлении эквивалентен переносу такого же “+” заряда в противоположном направлении. Если через поверхность одновременно переносится «+» и «¾» заряды, то

I = dq₊/dt + |dq_¾|/dt.

За направление тока принимается направление движения «+» носителей.

Эл. ток может быть распределен по поверхности, по которой он течет неравномерно. Это показывает вектор плотности тока j. Он численно равен отношению {силы тока dI, протекающего через расположенную в данной точке перпендикулярную к направлению движения носителей площадку dS_^} и {величины этой площадки}:

j = dI/dS_^, за его направление принимается u.

Ток, не изменяющийся по времени, называется постоянным:

I = q/t, где q – заряд, переносимый через рассматриваемую поверхность за конечное время t.

I = [A].

ЭДС:

Если в проводнике создать электрическое поле и не принимать мер к его поддержанию, то очень быстро ток прекратится. Для недопущения этого необходимо осуществлять круговорот зарядов по самкнутому пути. В замкнутой цепи должны иметься участки, на которых перенос положительных зарядов происходит в направлении возрастания j, т.е. против сил эл. поля. Перемещение носителей на этих участках возможно только под действием сторонних сил.

Их можно охарактеризовать работой, которую они совершают над перемещающимися по цепи зарядами. Величина, равная работе сторонних сил над единичным «+» зарядом, называется ЭДС.

e = A/q.

F_СТ = E*_*q, где Е* - напряженность поля сторонних сил.

Величина, равная работе, совершаемой электростатическими и сторонними силами при перемещении единичного «+» заряда, называется падением напряжения (напряжением):

U₁₂ = j1 - j2 + e₁₂.

Участок цепи, на котором не действуют сторонние силы, называется однородным, тогда:

U = j1 - j2.

Участок, на котором на носитель действуют сторонние силы, называется неотнородным.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

32. Закон Ома, сопротивление проводников, закон Джоуля – Ленца:

Закон Ома: сила тока, текущего по однородному металлическому проводнику, при отсутствии сторонних сил, пропорциональна падению напряжения U на проводнике.

I = (1/R)_*U, т.к. проводник однородный, то U = j1 - j2; R – электрическое сопротивление проводника.

[A] = [Ом]/[B].

Величина сопротивления зависит от формы, размеров и свойств материала проводника. Для однородного цилиндрического проводника:

R = r(l/S), где l – длина проводника, S – площадь поперечного сечения, r - удельное электрическое сопротивление, зависящее от свойств металла.

r = [Ом_*м].

В металлах направление векторов Е и j (плотность тока) совпадают. Из этого следует, что

j = (1/r)_*E = sE (закон Ома в дифференциальной форме), где s - удельная электрическая проводимость материала.

Закон Джоуля – Ленца:

Когда проводник неподвижен и химических превращений в нем не совершается, работа тока затрачивается на увеличение внутренней энергии проводника, в результате чего проводник нагревается, выделяется тепло:

Q = Uit = /по закону Ома/ = RI²t, закон получил название Джоуля – Ленца.

Если сила тока изменяется со временем, то кол-во теплоты за время t: Q = ₀ò^t RI²dt.

Кол-во тепла в элементарном цилиндрическом объеме:

dQ = RI²dt = ((rdl)/dS)(jdS)²dt = = rj²dVdt, где dV = dS_*dl.

Поделив выражение на dV и dt, получим кол-во теплоты, выделевшееся в ед. V за ед. t:

Q_УД = rj² – удельная тепловая мощность тока.

33. Закон Ома для для неонородного участка цепи:

На неоднородном участке цепи на носители тока действуют, кроме электрических сил еЕ, сторонние силы еЕ*, способные так же вызывать упорядоченное движение носителей тока. На таких участках:

j = s(E + E*) – закон Ома для неоднородного участка цепи в дифференциальной форме.

Для того, чтобы перейти от дифференциальной формы к интегральной:

Неоднородный участок цепи 1 – 2:

S

1 2

dL

Предположим, что значения j, s, E, E* в каждом сечении, ^ контуру 1–2, одинаковы; векторы j, E и Е* в каждой точке направлены по касательной к контуру.

Спроецировав на элемент контура dl векторы j, E и Е*, получим:

(*) j_L = s(E_L + E_L*), где проекции равуны модулю векторов, взятых со знаком «+» или «¾», в зависимости от направления вектора относительно dL.

Из-за сохранения заряда сила постоянного тока в каждом сечении будет одинаковой, то I = j_LS постоянна вдоль контура 1 – 2.

В (*) можно заменить: j = I/S, s = 1/r, то:

I(r/S) = E_L + E_L*, а по всей длине:

I₁ò²(r/S)dL = ₁ò²E_LdL + ₁ò²E_L*dL Û

Û IR = j1 - j2 + e₁₂ Û Û I = (j1 - j2 + e₁₂)/R – закон Ома для неоднородного участка цепи.

Если цепь замкнута, т.е. j1 = j2, то: I = e/R, где R – cуммарное сопротивление всей цепи.

34. Разветвление цепи. Правила Кирхгофа:

Узлом называется точка, в которой сходятся более, чем 2 проводника. Токи, текущие к и от одного узла, разноименны.

Первое правило: алгебраическая сумма токов, сходящихся в узле, равна 0:

åI_K = 0, что вытекает из закона сохранения заряда (суммарный заряд электрически изолированной системы не может изменяться), то поток вектора j должен быть равен 0.

Второе правило: рассмотрим контур:

() 2

R1 R2

e1 + + e2

¾

¾

() R3  ()