¾ + 3

1 ¾ + 3

Применим закон Ома:

I₁R₁ = j1 - j2 + e₁,

I₂R₂ = j2 - j3 + e₂, +

I₃R₃ = j3 - j4 + e₃,

I₄R₄ = j4 - j1 + e₄.

åI_KR_K = åe_K – II пр-ло.

I₁ I₂

I₃

R1 R2 R3

+ +

- -

 j1 0 j2

e1 e2

C

I₁R₁ + I₃R₃ = -e₁

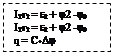I₁R₁ + I₂R₂ = -e₁ +e₂

35. Магнитное поле в вакууме:

Взаимодействие токов осуществляется через поле, называемое магнитным. Из опытов следует, что оно имеет направленный характер и должно характеризоваться векторной величиной, называемой магнитной индукцией (В), аналогичной величине Е в магнитном поле. Вспомогательную величину называют напряженностью магнитного поля (Н), аналогичной D электрического поля.

Магнитное поле, в отличие от электрического, не оказывает воздействия на покоящийся заряд. Сила возникает только когда заряд начинает двигаться.

Проводник с током представляет собой электрически нейтральную систему зарядов, значит магнитное поле пораждается толко движущимися зарядами.

Движущиеся заряды изменяют св-ва окружающего пространства, создавая в нем магнитное поле, проявляющегося в воздействии сил на движущиеся заряды.

Для магнитного поля так же справедлив и принцип суперпозиции:

Поле В, пораждаемое несколькими движущимися зарядами, равно векторной сумме полей B_i, пораждаемых каждым зарядом в отдельности; В = å B_i.

Для двух бесконечных ôô проводников сила их взаимодействия для единицы длины каждого из проводников равна:

f = k(2I₁I₂)/l, где l – расстояние между проводниками.

1А – такая сила неизменяющегося тока, проходящего по двум ôô проводникам, находящимся в вакууме на рассоянии в 1м, которая вызывает между проводниками силу, равную 2_*10^¾7Н/м.

1Кл – заряд, проходящий через сечение проводника за 1с и силе тока 1А.

f = [m₀/(4p)]_*(2I₁I₂)/l

2_*10^¾7 = [m₀/(4p)]_*2(1_*1)/1 ® ® m₀ = 4p_*10^¾7 (Гн/м).

Взаимодействие между токами осуществляется по средствам магнитного поля.

В качестве пробного элемента выбирается замкнутый контур.

® ®

I n

Ориентация контура может быть задана направлением нормали, определяемой методом «винта». За направление магнитного поля (В) так же принимается направление нормали.

a = 90^о ® m - мах;

a = 0 ® m = 0;

m_МАХ ~ I ü

ý m_МАХ ~ I_*S

m_МАХ ~ S þ ® ®

Устан.момент магн. диполя: P_M=I_*S_*n

m_MAX/P_M ~ B.

36. Закон Био – Савара:

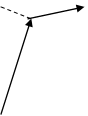
Величина напряженности должна зависеть от силы тока в проводнике, от расстояния от наблюдаемой точки до проводника и от угла наклона.

I

dB

r

a

dl

®

Можно определить Н в некой точке:

® ®

dH = k(I[dl x dr])/r³ – закон Био – Савара – Лапласса, позволяющий вычислить напряженность для любых условий.

[H] = А/м; [B] = Тл.

I

(X)

a

da

®

r

dr

dL

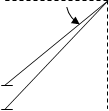
dH = k(I_*dL_*sina)/r²

dL = dr/sina = rdr/sina = bda/sin²a

r² = b²/sin²a

dH = I/(4p)_*(bda)/sin²a_*(sin²a/b²)_*sina = = I/(4p)_*(sina da)/b;

p

H = I/(4pb) ₀ò sina da = I/(2pb);

H = I/(2pb) – частный случай.

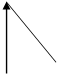
I

a1

a2

H = [I/(4pb)]_*(cosa1-cosa2)

37. Поле прямого и кругового тока:

I

(X)

a

da

®

r

dr

dL

dH = k(I_*dL_*sina)/r²

dL = dr/sina = rdr/sina = bda/sin²a

r² = b²/sin²a

dH = I/(4p)_*(bda)/sin²a_*(sin²a/b²)_*sina = = I/(4p)_*(sina da)/b;

p

H = I/(4pb) ₀ò sina da = I/(2pb);

H = I/(2pb) – частный случай.

I

a1

a2

H = [I/(4pb)]_*(cosa1-cosa2)

Линии магнитной индукции магнитного поля прямого тока представляют собой систему охватывающих провод концентрических окружностей.

 ®

 I

Поле кругового тока:

®

® dH

dl R r

X

dH = 1/(4p)_*(Idl)/R²

2pR

H = I/(4pR)_*0ò dl = I/(2R)

dH_ôô = dH sina = dH(R/r)

dH_ôô = 1/(4p)_*(Idl)/r²_*R/r

H_ôô = 1/(4p)_*(2pR²I)/r³ = = 1/(4p)_*(2pm)/r ³, x >> R ®

® H_ôô = 1/(4p)_*(2pm)/x³

H_ôô = 1/2_*(2pR³I)/(R² + x²)^3/2, если (x >> R).

®

H₁

®

 H_å

®

H H₂

® ®

I I

1 2

Напряженность магнитного поля, создаваемая круговыми токами на точке плоскости, относительно которой витки симметричны, будет ориентирована ôô оси витков.

38. Поле соленоида:

Соленоид – цилиндрический каркас бесконечной длины с намотанным на него проводом.

®

I

1 2

1’ 2’

® ® 4 3

oòH dl = ₁ò²Hdl + ₂ò³Hdl + ₃ò⁴Hdl + + ₄ò¹Hdl;

H₁ò²dl = H_*l = Inl;

H = I_*n, где n – плотность обмотки.

Поле внутри соленоида однородно.

Поле снаружи соленоида равно 0.

H_{1’ 2’} = 0.

39. Сила Лоренца. Закон Ампера:

На заряд, движущийся в магнитном поле, действует сила, называемая магнитной и определяемая зарядом q, скоростью движения v и магнитной индукцией В. Направление вектора F определяется направлением v и В.

® ® ®

F = q_*[v x B];

Это выражение было получено Лоренцем путем обобщения экспериментальных данных и получило название силы Лоренца.

®

F_¶

® ®

B₁ q₁ v₁

(_*) ( )

®

B₂  ®

(x) ( ) v₂

q₂

®

F_¶

® ® ®

F_Л = q_*[v x B];

® ® ® ®

F_Л = q_*[v x B] + q_*E

F = 1/(4pe)_*(q₁q₂)/r²

F_Л = qvB = qv_*(m₀/4p)_*(v/r₂)_*q₂ (?)

B₂ = m₀/(4p)_*(I₂dl)/r² = = m₀/(4p)_*(q₂/dt)_*(dl/r²) = m₀/(4p)_*(q₂v)/r²

F_Л/F_¶ = m₀e₀v² = v²/C².

Закон Ампера:

® ® ® ®

F = e [(u + u), B];

u - тепловая скорость;

u – скорость направленного движения;

 ® ® ®

<F> = e [<u>, B];

dV = S_*dl;

® ® ® ®

F = <F>_*nS_*dl = en [<u>, B] S_*dl;

® ®

en <u> = j;

® ® ®

F = [j, B] dV;

® ® ® ®

F_{ЕД. ОБ.} = F/dV = [j x B];

® ®

j_*S_*dl = I_*dl;

 ® ® ®

dF = I [dl x B] – сила Ампера.

40. Контур с током в магнитном поле, вращательный момент:

a

 b ®  ® ®

F_A F_A B

^{(x) (*)}

I

F_A = IaB

M = IabB = ISB = P_MB, где Р_М – магнитный момент. (?) ®

F_A

b ®

F_A

 a

® ®

(X) n (X) B

®

F_A

®

F_A

® ® ®

F = I [l x B];

® ® ®

M = [P_M B];

Контур произвольной формы:

dh

dl₁ dl₂ ®

B

®

 I

I_a

® a₁ ®

dl₁(X)F_Л dl₂(_*) F_Л ®

® a₂ B

I

dF₁ = I dl₁B sina₁ = IB dh

dF₂ = I dl₂B sina₂ = IB dh

dM = dF_*a = Iba dh = IB dS

M = ISB = P_MB

® ® ®

M = [P_M B]

dA = M da = P_MB sina da

dA = dW_p

A = W_p = ₀ò^aM da = -P_MB cosa + const – потенциальная энергия контура с током в магнитном поле.

a = p/2 ® W_p = const = 0

W_p = -P_MB cosa = -(P_M B)

41. Работа по перемещению контура с током в магнитном поле:

®

I

®

+ I

 l

¾ ® F_A

(X) B

®

I dx

dA = F_A dx = IB (l dx) = IB dS = I dФ;

dФ – поток магнитной индукции, пересекаемый проводником.

Если В (вектор) не ^ контуру, то

dA = Ibl cosa dx = IBn dS = I dФ, т.к.

dФ = B dS = B cosa dS = Bn dS

На совершение работы идет ресурс источника тока, его ЭДС.

Индукционный поток направлен противоположно току I.

1 2

® ®

I I

Ф_Н ® Ф₀ Ф_К

(X) B

 

 2  2

A₁ = I (Ф_Н – Ф₀)

А₂ = I (Ф₀ – Ф_K) (?)

A = A₁ + A₂ = I (Ф_К – Ф_Н) = I DФ.

®

I

®

 (X) B

A = -IBS – IBS = -2IBS.

42. Магнитное поле в веществе:

Первоначально поле в вещ-ве рассматривалось как поле от микротоков.

Движение зарядов обуславливает магнитный момент и они рассматриваются как некая система.

® ® ®

B = B₀ + B’.

Введем вектор, характеризующий магнитные св-ва и связанный с (_i=1å^NP_Mi)/DV:

®

J = (_i=1å^NP_Mi)/DV

[ J ] = A/м;

J = c H, где c - магнитная восприимчивость.

c_УД = c/r = [м ³/кг], где r - плотность вещ – ва.

c_МОЛ = c_*n_Кмоль [м³/Кмоль].

44. Описание магнитного поля в магнетике:

Существует 3 класса магнетиков:

1) Диамагнетики (c_МОЛ < 0, 10^¾7¸10^¾8 (м³/Кмоль));

2) Парамагнетики (c_МОЛ > 0, 10^¾6¸10^¾7 (м³/Кмоль));

3) Ферромагнетики (c_МОЛ < 0, 10³¸10⁴ (м³/Кмоль)).

Электрическое поле в веществе может только ослабляться. В магнитном поле оно либо усиливается, либо ослабляется.

® ® ® ® ®

H = B/m₀ – J = B/m₀ - cH

® ®

H(1 + c) = B/m₀

® ®

H = B/(m₀m); m = 1 + c.

Внесем в магнитное моле магнетик:

®

B₀

(X)(X)

(X)(X)

(X)(X) B’

 

dl микротоки

® ® ®

B = B₀ + B’

B’ = m_0*I_l

dP_M = I_l*S_*dl

dP_M/dV = J = I_l

® ® ®

B = B₀ + m₀J

® ® ® ® ®

H = B/m₀ – J = B₀/m₀ = H₀ (теоретически)

® ® ®

H = H₀ – H₀, где Н₀ – размагничивающее поле;

® ®

H₀ = N_*J (фактор размагничивания)

N = 1 для тонкого диска;

N = 1/3 для шарика.

Если однородный магнетик помещается во внешнее однородное поле, то внутреннее поле магнетика так – же будет однородным.

45. Поведение векторов В и Н на границе двух магнетиков:

®

n ®

B

m₁

b

m₂

®

n

oò BdS = -Bn₁S + Bn₂ + <Bn>S_БОК = 0, где (<Bn>S_БОК) = 0;

B₁n = B₂n

Компонента вектора индукции магнитного поля неприрывна.

m₀m₁H₁n = m₀m₂H₂n

H₁n/H₂n = m₂/m₁

a₁

m₁ I a

b

m₂ I

a₂

m₁ > m₂

® ®

oòH dl = H₁t_*a - H₂t_*a + <H>_*2b = 0

H₁t = H₂t

B₁t/(m₀m₁) = B₂t/(m₀m₂) Û B₁t/B₂t = = m₁/m₂

tg a₁/tg a₂ = m₁/m₂.

46. Магнитные механические явления:

Представления Бора:

u

® ®

M r P_M

 

е

I = en = e (w/2p) = e [u/(2pr)] – величина силы тока, создаваемого электронами.

L = Jw = mr²_*u/r = mur – механический момент. (m - ?)

Замена L ® M:

P_M = IS = I_*pr² = (eur)/2 – магнитный момент.

P_M/M = -l/(2m) – гиромагнитное отклонение.

åM ¹ 0 – суммарный механический момент электронов.

-åM_i ¹ 0 – суммарный механический момент атомов.

Магнетик в магнитном поле приобретает отличные от нуля суммарные механические моменты атомов и электронов, в вследствие чего он начинает вращаться, что приводит к намагничиванию магнетика.

Собственный механический момент:

~

M_S = h/2 – этому кратен собственный механический момент для электрона.

~

h = h/2p = 1,05_*10^{– 34} (Дж_*с)

Собственный механический момент (спин) равен половине постоянной Планка (h), которая играет роль элементарного магнитного импульса.

Собственный магнитный момент:

P_MS/M_S = - l/m;

~

P_MS = - (l h)/(2m);

~

m_Б = (l h)/2m – магнетон Бора.

Каждый атом, его магнитный момент складывается из орбитальных и силовых моментов электронов.

Было исследовано поведение атомов в магнитном поле:

F = P_M (¶B/¶x) cos(a), a - угол между направлением магнитного момента и индукцией. Магнитные моменты атомов имеют произвольные углы ориентации.

48. Пара- и ферромагнетики:

У парамагнетиков магнитная восприимчивость немногим > 0.

m у парамагнетиков мало отличается от 1.

У ферромагнетиков (железо, никель, кобальт и др.) магнитная восприимчивость » 10¹⁰ раз больше, чем у парамагнетиков.

У ферромагнетиков:

 J

H

 B

H_C

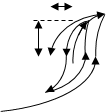
B_ОБ

H

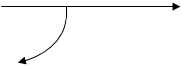
m

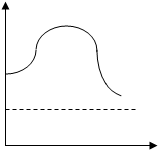
H

 

49. Электромагнитная индукция, ЭДС индукции, токи Фуко:

В электропроводящем контуре при изменении проходящего через него потока возникает ток, независящий от способа изменения потока, и называемый индукционным. В контуре так же возникает ЭДС.

I_ИНД = dФ/dt (скорость изменения потока).

Если контур заполнен магнетиком с проницаемостью m, то это приводит к увеличению потока в m раз.

Правило Ленца:

Индукционный ток I имеет такое направление, чтобы препятствовать причине, его вызывающей.

ЭДС индукции:

®

I

®

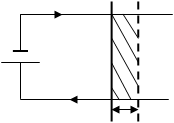
(X) n ®

e +  R u

¾ ®

(X) B

®

I

DФ

Ie dt = dA – работа сторонних сил внутри источника.

Если R неподвижен, то dQ =I²R dt – тепло, выделяющееся в R, dA = dQ.

Если R перемещается, то

dA = dQ + I dФ

eI dt = I²R dt + I dФ

I = (e - dФ/dt)/R.

Поток магнитной индукции Ф измеряется в веберах (Вб).

e_i = - dФ/dt.

Если витков несколько:

Ф ® y = N_*Ф₁

e_i = -dy/dt = -N(dФ₁/dt), где y - потокосмещение.

При перемещении проводника с током:

®

(X) B

(e)

F_И ®

U ®

u

®

F_Л

 ® ® ® ®®

dA = F_ЛU dt + F_И u dt

dA = F_Л U dt - F_И u dt = e u B U dt - - e U B u dt = 0.

Токи Фуко:

Возникают в проводах, по которым текут переменные токи. Направлены они так, что ослабляют токи внутри провода и усиливают их внутри поверхности. В результате быстропеременный ток оказывается распределенным по сечению проводника неравномерно, он как бы вытесняется на поверхность проводника. Это явление называется скин – эффектом. Из-за него внутренняя часть в высокочастотных проводниках оказывается бесполезной, и обычно такие проводники представляют из себя трубки

Токи Фуко приводят к тепловым потерям. Используются в индукционных печах.

50. Явление самоиндукции:

Если по проводнику течет ток, то его контур пронизывает магнитный поток.

Ф ® y (y - потокосмещение);

y ~ B ~ I ® y = L_*I

L – коэффициент пропорциональности (индуктивность). Определяется геометрическими размерами контура, у ферромагнетиков еще и материалом среды.

Если контур жесткий и не может быть деформирован, то L – const.

Индуктивность солинойда:

B = m₀mnI (n – число витвов на единицу длины);

Ф = BS, y = ФN = m₀mnISnl = = m₀mn²IV;

L = m₀mn²V, где V – объем соленоида.

Возникает самоиндукция:

e_S = -dy/dt = -(L_*dI/dt + I_*dL/dt) – ЭДС самоиндукции;

L – const, то e_S = -L_*dI/dt.

51. Энергия магнитного поля:

L

R

В центре всегда есть индуктивность, скорость установления тока всегда конечна.

dA = e_SI dt = /- любая совершаемая работа/ = -dy/dt Idt = -dyI, где dy - величина изменения потока за время dt.

dy = L dI

dA = -LI dI;

A переходит в ленц - джоулевое тепло, выделяемое в проводах схемы.

0

A = òdA = -L ò I dI = LI²/2.

I₀

L = m₀mn²V

H = nI

A = W = LI²/2 = 1/2_*(m₀mH²)_*V

W – энергия маг. поля в соленоиде.

W/V = w_H = 1/2_*(m₀mH²) = BH/2 = = B²/(2m₀m).

52. Уравнения Максвелла:

Открытие тока смещения позволило Максвеллу создать единую теорию электрических и магнитных явлений, объяснившую многие из экспериментальных фактов и предсказала новые. Основным стал вывод о существовании электромагнитных волн, распространяющихся со скоростью света, что привело Максвелла к созданию электромагнитной теории света.

Основой теории стали уравнения Максвелла. Первую пару уравнений образуют:

[DE] = -¶B/¶t (связывает значение Е с изменениями вектора В во времени);

DВ = 0 (указывает на отсутствие источников магнитного поля, т.е. магнитных зарядов).

Вторая пара:

[DH] = j + ¶D/¶t (устанавливает связь между токами проводимости и смещения и порождаемым ими магнитным полем);

DD = r (показывает, что источником вектора D служат сторонние заряды).

Для расчета полей нужно дополнить имеющиеся уравнения уравнениями, связывающими D и j c E, a так же H c B:

D = e₀eE;

B = m₀mH;

j = sE.

Перечисленные уравнения Максвелла и их дополняющие образуют основу электродинамики покоящихся сред.

Уравнения Максвелла в дифференциальной форме:

Первая пара:

о_Гò E dl = -d/dt _SòBdS (закон эл.-маг. индукции Фарадея, получается путем интегрирования ур-я в диф. форме с; последующим преобразованием левой части в интеграл с контуром Г, ограничивающему поверхность S)

o_SòBdS = 0 (отсутствие магнитных зарядов);

Вторая пара:

о_ГòHdl = _SòjdS + d/dt _SòDdS (теорема полного тока);

o_SòDdS = _Vòr dV (теорема Гаусса).