Волновая функция и волновое уравнение

2.1.3. Волновая функция и волновое уравнение.

Так как электронам присущи волновые свойства и они обладают неопределенностью положения в пространстве, их движение характеризуется при помощи волновой функции и описывается волновым уравнением. Физический смысл волновой функции заключается в том, что ее квадрат ² пропорционален вероятности нахождении электрона в элементарном объеме атома V с координатами x, y, z.

Значение волновой функции находят при решении волнового уравнения Шредингера:

²/x² + ²/y² +²/z² +82m/h²*(E–U)=0

В этом сложном дифференциальном уравнении с частными производными: Е–полная энергия частицы, U – потенциальная энергия, –волновая функция.

Волновая функция, получаемая при решении уравнения Шредингера, может иметь ряд значений. Эти значения зависят от квантовых параметров n, l, m_e, названных квантовыми числами

n

 l

m_e

В итоге – значения квантовых чисел есть не что иное как результат решения уравнения Шредингера. Следовательно, при решении уравнения Шредингера получены значения волновой функции и возможные /допустимые/ значения квантовых чисел.

2.1.4. Квантовые числа. Атомные орбитали.

Так как электрон имеет четыре степени свободы, то для характеристики его поведения в атоме требуется четыре квантовых числа.

Главное квантовое число n определяет удаленность атомной орбитали от ядра и характеризует общий запас энергии электрона на данном энергетическом уровне. n принимает целочисленные значения от единицы до бесконечности. В зависимости от цифровых значений главного квантового числа приняты буквенные обозначения квантовых уровней n=1, 2, 3, 4,…

обозначение К, L, M, N,…

Чем больше n, тем слабее электрон связан с ядром и более емким становится квантовый уровень. Числовые значения n определяют также и количество подуровней, содержащееся на данном квантовом уровне /т.е. числовые значения n определяют емкость квантового уровня/. Так, если n=3, то это значит, что имеем третий квантовый уровень, который состоит из трех подуровней.

Орбитальное квантовое число l характеризует момент количества движения электрона относительно центра орбитали. Наличие такого движения приводит к делению квантового уровня на подуровни. Орбитальное квантовое число характеризует так же пространственную форму электронного облака. Это квантовое число предопределяется главным квантовым числом n и принимает ряд целочисленных значений от нуля до n–1. В зависимости от числовых значений l приняты буквенные обозначения подуровней:

n=1, 2, 3, 4,…

l=0, 1, 2, 3,…,–1

обозначение подуровня: s, p, d, f,…

форма орбитали

Магнитное квантовое число m_l характеризует магнитный момент электрона. Определяет ориентацию квантового подуровня в пространстве. Число проекций подуровня на направление магнитных силовых линий квантуется и оно равно количеству орбиталей на данном подуровне. Можно сказать, что магнитное квантовое число определяет количество орбиталей на подуровне. m_l принимает значения от –l через ноль до +l.

m_l = –l,…,+1, 0, –1,…, +l.

Рассмотрим подуровень s. Для него: l=0, m_l=0

H рис.2.1.

У подуровня шарообразной формы может быть только одна проекция. (рис.2.1.), имеющая значение «ноль». Следовательно, на s -подуровне только одна s-орбиталь.

Подуровень Р имеет l=1, а m_l = –1, 0, +1

l=1

В данном случае согласно правил квантования уже три проекции.

Следовательно на р-подуровне три р-орбитали. рис2.2.

Для d-подуровня: l=2, m_l = –2, –1, 0, +1, +2. Это значит, что согласно квантовой теории d-подуровень состоит из пяти d-орбиталей.

Подуровень f имеет l=3, m_l = –3, –2, –1, 0, +1, +2, +3. Следовательно f-подуровень состоит из семи f-орбиталей.

Число орбиталей на подуровне можно определить из выражения m_l =2l+1:

значение l: 0, 1, 2, 3, …….

подуровень: s, p, d, f, …….

число орбиталей: 1, 3, 5, 7, …….

Спиновое квантовое число m_s характеризует собственный момент количества движения, возникающий как бы из-за «вращения» электрона вокруг собственной оси. Принимает два значения: +1/2 и –1/2, что соответствует двум возможным направлениям вращения электрона.

m_s= +1/2; –1/2.

Оно получено из опытов Штерна и Герлаха.

Рассмотренные квантовые числа определяют энергию электрона, объем и форму пространства, в котором вероятно его пребывание в околоядерном объеме, т.е. размер, форму и ориентацию орбитали в пространстве.

Так как волновая функция является решением уравнения Шредингера при всевозможных значениях квантовых чисел, то можно сказать, что волновая функция является в свою очередь функцией рассмотренных квантовых параметров n, l и m_l, где:

n= 1, 2, 3, 4,…,

l= 0, 1, 2, 3,…,n–1

m_l=–l,…, –1, 0, +1,…, +l

Атомные орбитали. Так как вероятность нахождения электрона в пространстве далеком от ядра очень мала, когда говорят об орбиталях, то имеют в виду такую область вокруг ядра атома внутри которой сосредоточено 90–95% электронного заряда. С точки зрения квантовой механики атомные орбитали являются геометрическим изображением волновой функции  (n, l, m_l).

Z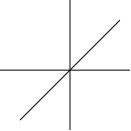 Электронное облако. Если бы в каждый момент времени

y определяли положение электрона в трехмерном пространстве и

ставили в том месте точку, то через множество таких определений

X получили бы картину в виде пространственного облака изображен-

ного точками с размытыми краями /рис.2.3.)

рис.2.3.

Такое зарядовое облако называют электронным облаком. Его плотность, пропорциональная ², является непосредственной мерой вероятности нахождения электрона. Граничная поверхность облака, внутри которой содержится 90–95% электронного заряда, дает форму орбитали.

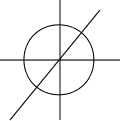Z s-орбиталь. Она существует при l=0. Значение m_l тоже равно

Y нулю. Имеем только одно значение m_l =0. Следовательно,

s-орбиталь имеет максимальную симметричность. У нее

X сферическая форма (рис.2.4.). В этом случае вероятность на–

хождения электрона в околоядерном пространстве определя–

рис.2.4. ется только радиусом-вектором и не зависит от угла координат.

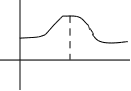 Радиальное распределение электронной плотности для 1s

электрона соответствует кривой с максимумом (рис.2.5.).

Максимум распространения вероятности находится на

0 r₁ r,A⁰ расстоянии от ядра r₁, которые соответствует радиусу

рис.2.5. первой боровской орбиты.

р-орбиталь. Существует при l=1. m_l = –1, 0, +1.

Z р-орбиталь появляется на втором и всех последующих

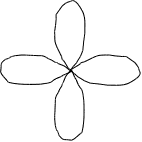
Рz уровнях. Так как m_l имеет три значения, то на р-подуров-

Y не каждого уровне может быть три р-орбитали. р-орбиталь

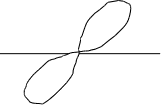имеет гонтелеобразную форму. Все три р-орбитали распо-

X лагаются в пространстве по направлению координатных

Px осей. Их называют соответственно р_х, р_y, р_z-орбитали

Py (рис.2.6.).

Р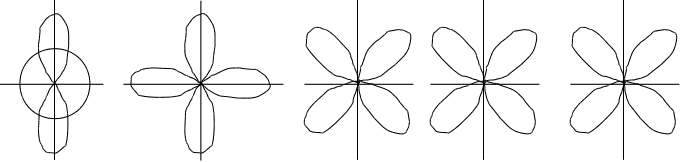ис.2.6. Z Y Y Z Z

X X X X Y

dz² dx² y² dxy dxz dyz

рис.2.7.

d-орбиталь. Появляется при l=2 на третьем квантовом уровне. На d-подуровне может быть уже пять различных состояний электронов, поэтому на d-подуровне каждого квантового уровня содержится пять d-орбиталей. В этом случае m_l принимает пять значений: m_l = –2, –1, 0, +1, +2, d-орбитали имеют более сложную форму, чем р-орбитали, они либо в виде четырех лепестков либо в виде гантели с ободком (рис.2.7.).

f-орбиталь. Появляется при значении l=3. f-орбитали могут быть только на четвертом и более отдаленных уровнях. Так как при l=3 m_l имеет 7 значений /–3, –2, –1, 0, +1, +2, +3/, то на f-подуровне может быть семь орбиталей. Форма f-орбиталей еще более сложная, чем у d-орбиталей. f-орбитали изображают в виде сложных шестилепестковых фигур.

Форма орбиталей и ее направленность играют существенную роль при образовании химических связей, т.к. эти два фактора определяют характер и степень перекрывания электронных облаков соединяющихся атомов.