Навигация
Методы прогнозирования финансовых показателей
1.Модель с аддитивной компонентой
Аддитивную модель прогнозирования можно представить в виде формулы:
F = T + S + E
где: F – прогнозируемое значение; Т – тренд; S – сезонная компонента;
Е – ошибка прогноза.
Алгоритм построения прогнозной модели
Для прогнозирования объема продаж, имеющего сезонный характер, предлагается следующий алгоритм построения прогнозной модели:
1.Определяется тренд, наилучшим образом аппроксимирующий фактические данные. Существенным моментом при этом является предложение использовать полиномиальный тренд, что позволяет сократить ошибку прогнозной модели.
2.Вычитая из фактических значений объёмов продаж значения тренда, определяют величины сезонной компоненты и корректируют таким образом, чтобы их сумма была равна нулю.
3.Рассчитываются ошибки модели как разности между фактическими значениями и значениями модели.
Применение алгоритма рассмотрим на следующем примере.
Исходные данные: Объемы фактических расходов бюджета _________ района, взяты из месячной и годовой отчетности финансового управления администрации ________ района. Данная статистика характеризуется тем, что значения объёма продаж имеют выраженный сезонный характер с возрастающим трендом. Исходная информация представлена в табл. 1.
табл.1
| Объем фактических расходов | |
| 1 кв. 1999 г. | 24518 |
| 2 кв. 1999 г. | 23778 |
| 3 кв. 1999 г. | 25143 |
| 4 кв. 1999 г. | 27622 |
| 1 кв. 2000 г. | 26149 |
| 2 кв. 2000 г. | 24123 |
| 3 кв. 2000 г. | 27580 |
| 4 кв. 2000 г. | 30854 |
| 1 кв. 2001 г. | 29147 |
| 2 кв. 2001 г. | 26478 |
| 3 кв. 2001 г. | 30159 |
| 4 кв. 2001 г. | 33149 |
| 1 кв. 2002 г. | 32451 |
Реализуем алгоритм построения прогнозной модели, описанный выше. Решение данной задачи рекомендуется осуществлять в среде MS Excel, что позволит существенно сократить количество расчётов и время построения модели.
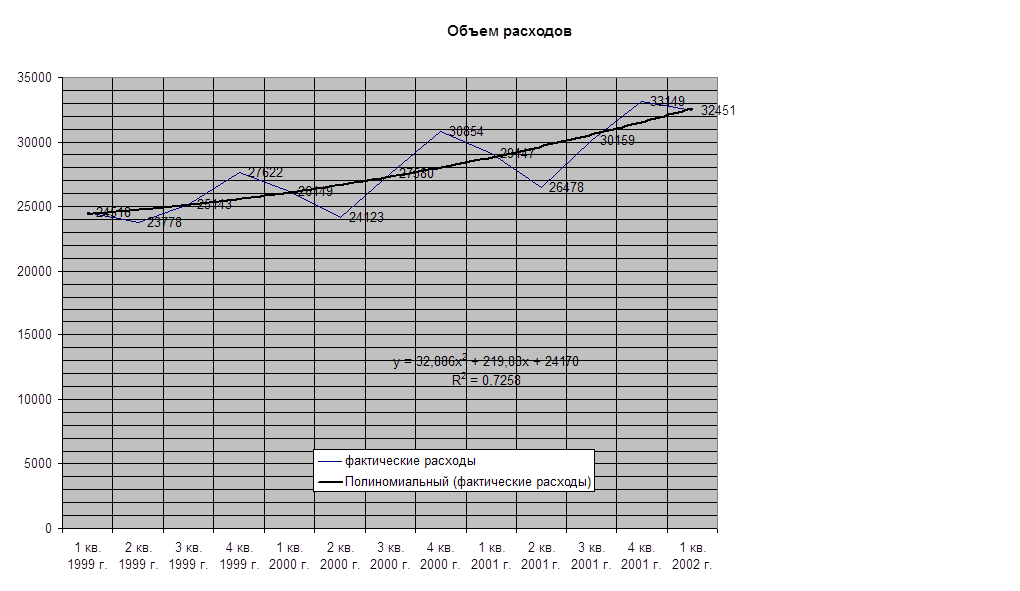 1. Определяем тренд, наилучшим образом аппроксимирующий фактические данные. Для этого рекомендуется использовать полиномиальный тренд, что позволяет сократить ошибку прогнозной модели)
1. Определяем тренд, наилучшим образом аппроксимирующий фактические данные. Для этого рекомендуется использовать полиномиальный тренд, что позволяет сократить ошибку прогнозной модели)
Таблица 2.
Расчёт значений сезонной компоненты
| Значение тренда | Сезонная компонента | ||
| 1 кв. 1999 г. | 24518 | 24518 | 0 |
| 2 кв. 1999 г. | 23778 | 24962 | -1184 |
| 3 кв. 1999 г. | 25143 | 25012 | 131 |
| 4 кв. 1999 г. | 27622 | 25217 | 2405 |
| 1 кв. 2000 г. | 26149 | 26098 | 51 |
| 2 кв. 2000 г. | 24123 | 26958 | -2835 |
| 3 кв. 2000 г. | 27580 | 27495 | 85 |
| 4 кв. 2000 г. | 30854 | 28017 | 2837 |
| 1 кв. 2001 г. | 29147 | 28964 | 183 |
| 2 кв. 2001 г. | 26478 | 29617 | -3139 |
| 3 кв. 2001 г. | 30159 | 30498 | -339 |
| 4 кв. 2001 г. | 33149 | 31485 | 1664 |
| 1 кв. 2002 г. | 32451 | 32451 | 0 |
Скорректируем значения сезонной компоненты таким образом, чтобы их сумма была равна нулю.
| Таблица 3. Расчет средних значений сезонной компоненты | ||||||
| 1999 г. | 2000 г. | 2001 г. | Итого | Среднее | Сезонная компонента | |
| 1 кв. | 0 | 51 | 183 | 234 | 78 | 89,75 |
| 2 кв. | -1184 | -2835 | -3139 | -7158 | -2386 | -2374,25 |
| 3 кв. | 131 | 85 | -339 | -123 | -41 | -29,25 |
| 4 кв. | 2405 | 2837 | 1664 | 6906 | 2302 | 2313,75 |
| Сумма | -47 | 0 | ||||
| -11,75 | ||||||
3. Рассчитываем ошибки модели как разности между фактическими значениями и значениями модели.
Таблица 4.
Расчёт ошибок
| расходы | Значение модели | Отклонение | |
| 1 кв. 1999 г. | 24518 | 24607,75 | -89,75 |
| 2 кв. 1999 г. | 23778 | 22587,75 | 1190,25 |
| 3 кв. 1999 г. | 25143 | 24982,75 | 160,25 |
| 4 кв. 1999 г. | 27622 | 27530,75 | 91,25 |
| 1 кв. 2000 г. | 26149 | 26187,75 | -38,75 |
| 2 кв. 2000 г. | 24123 | 24583,75 | -460,75 |
| 3 кв. 2000 г. | 27580 | 27465,75 | 114,25 |
| 4 кв. 2000 г. | 30854 | 30330,75 | 523,25 |
| 1 кв. 2001 г. | 29147 | 29053,75 | 93,25 |
| 2 кв. 2001 г. | 26478 | 27242,75 | -764,75 |
| 3 кв. 2001 г. | 30159 | 30468,75 | -309,75 |
| 4 кв. 2001 г. | 33149 | 33798,75 | -649,75 |
| 1 кв. 2002 г. | 32451 | 32540,75 | -89,75 |
Находим среднеквадратическую ошибку модели (Е) по формуле:
Е= Σ О2 : Σ (T+S)2
где:
Т- трендовое значение объёма расходов;
S – сезонная компонента;
О- отклонения модели от фактических значений
Е=(3079106/(361151*361151))*100% = 0,002361%
Величина полученной ошибки позволяет говорить, что построенная модель хорошо аппроксимирует фактические данные, т.е. она вполне отражает экономические тенденции, определяющие объём расходов, и является предпосылкой для построения прогнозов высокого качества.
Похожие работы
... трех месяцев со дня наступления сроков платежей. Оценку вероятности банкротства можно провести с помощью финансового анализа, так как именно он располагает широким арсеналом средств по прогнозированию банкротства предприятия и дает возможность заблаговременно продумать и реализовать меры по выходу предприятия из кризисной ситуации. Финансовое состояние предприятия представляет собой отражение ...
... : - долгосрочные; - среднесрочные; - краткосрочные; 8. По степени локализации периода: - точечные; - интервальные; 9. По характеру изменения объекта прогнозирования: - непрерывные; - дискретные. Особенности экономических прогнозов: - представляет его аргументированное заключение о будущих изменениях; - ...
... Счет операций с капиталом (счет накопления); 4. Платежный баланс – счет операций по взаимодействию с внешним миром. По каждому из этих четырех счетов возможны детализации. 2.3 Методы прогнозирования макроэкономических показателей и экономического роста В настоящее время существует приблизительно 150 методов прогнозирования, но на практике используются около 20-30 основных методов. Метод ...
... на платные работы и услуги существенно отличаются от данных баланса и имеют гораздо меньшие темпы роста в действительности. 2.2. Анализ структуры стоимости имущества предприятия и средств вложенных в него. Анализ финансовой деятельности специализированного строительного управления за период 1999-2000 года проводится по данным бухгалтерского баланса, отчёта о финансовых результатах и их ...


0 комментариев