Навигация
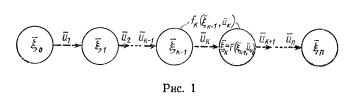
Управление системы S в графическом изображении
рис.2.2
В общем случае, когда состояние системы описывается n параметрами xi (i=1,2,…,n), областью возможных состояний служит n-мерное пространство, а уравление изображается перемещением точкиS из какой-то начальной области S0 в конечную Skпо некоторой “траектории” этого пространства.
Таким образом, задаче динамического программирования можно дать следующую геометрическую интерпретацию. Из всех траекторий, принадлежащих области возможных состояний системы и соединяющих области S0 и Sk , необходимо выбрать такую, на которой критерий W принимает оптимальное значение.[7].
Чтобы рассмотреть общее решение задач динамического программирования, введем обозначения и сделаем для дальнейших изложений предположения.
Будем считать, что состояние рассматриваемой системы S на K-м шаге (k=1,n) определяется совокупностью чисел X(k) =(x1 (k) , x2(k) ,…, xn(k) ), которые получены в результате реализации управления uk, обеспечившего переход системы S из состояния X(k-1) в состояние X(k). При этом будем предполагать, что состояние X(k) , в которое перешла система S , зависит от данного состояния
X(k-1) и выбранного управления uk и не зависит от того, каким образом система S пришла в состояние X(k-1) .
Далее будем считать, что если в результате реализации k-го шага обеспечен определенный доход или выигрыш, также зависящий от исходного
состояния системы X(k-1) и выбранного управления uk и равный Wk(X(k-1), uk), то общий доход или выигрыш за n шагов составляет
n
F=∑ Wk(X(k-1), uk ). (2.1)
k=1
Таким образом, задача динамического программирования должна удовлетворять два условия. Первое условие обычно называют условием отсутствия последействия, а второе – условием аддитивности целевой функции задачи.
2.2 Информационно-методическое обеспечение метода
Выполнение для задачи динамического программирования первого условия позволяет сформулировать для нее принцип оптимальности Беллмана. Прежде чем сделать это, надо дать определение оптимальной стратегии управления. Под такой стратегией понимается совокупность управлений U*=(u1*, u2*, …, un*), в результате реализации которых система S за n шагов переходит из начального состояния X(0) в конечное X(k) и при этом функция (2.1) принимает наибольшее значение.
Принцип оптимальности: какое бы не было состояние системы перед очередным шагом, надо выбрать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным.
Отсюда следует, что оптимальную стратегию управления можно получить, если сначала найти оптимальную стратегию управления на n-м шаге, затем на двух последних шагах, затем на трех последних шагах и т.д., вплоть до первого шага. Таким образом, решение рассматриваемой задачи динамического программирования целесообразно начинать с определения оптимального решения на последнем, n-м шаге. Для того чтобы найти это решение, очевидно, нужно сделать различные предположения о том, как мог окончиться предпоследний шаг, и с учетом этого выбрать управление un0 , обеспечивающее максимальное значение функции Wn(X(n-1), un). Такое управление un0 выбранное при определенных предположениях о том, как окончился предыдущий шаг, называется условно оптимальным управлением. Следовательно, принцип оптимальности требует находить на каждом шаге условно оптимальное управление для любого из возможных исходов предшествующего шага.
Чтобы это можно было осуществить практически, необходимо дать математическую формулировку принципа оптимальности. Для этого введем некоторые дополнительные обозначения. Обозначим через Fn(X0) максимальный доход, получаемый за n шагов при переходе системы S из начального состояния X(0) в конечное состояние X(k) при реализации оптимальной стратегии управления U=(u1, u2, …, un), а через Fn-k(X(k)) –максимальный доход, получаемый при переходе из любого состояния X(k) в конечное состояние X(n) при оптимальной стратегии управления на оставшихся n-k шагах. Тогда:
Fn(X0)=max[W1(X(0), u1)+…+ Wn(X(n-1), un)]; (2.2)
Uk+j
Fn-k(X(k))=max[Wk+1(X(k), uk+1)+Fn-k-1(Xk+1))](k=0, n-1). (2.3)
Uk+1
Последнее выражение представляет собой математическую запись принципа оптимальности и носит название основного функционального уравнения Беллмана или рекуррентного соотношения. Используя данное уравнение можно найти решение задачи динамического программирования.
Полагая k=n-1 в рекуррентном соотношении (2.3) , получим следующее функциональное уравнение:
F1(X(n-1)=max[Wn(X(n-1), un)+F0(X(n))]. (2.4)
un
В этом уравнении F0(X(n)) будем считать известным. Используя теперь уравнение (1.4) и рассматривая всевозможные допустимые состояния системы S на (n-1)-м шаге X1(n-1), X2(n-1), …, Xm(n-1), …, находим условные оптимальные решения
un0(x1(n-1)), un0(x2(n-1)),…, un0(xm(n-1)),…
и соответствующие значения функции (2.4)
F10 (X1(n-1)), F10 (X2(n-1)), …, F10 (Xm(n-1)),… .
Таким образом, на n-м шаге находим условно оптимальное управление при любом допустимом состоянии системы S после (n-1)-го шага. То есть, в каком бы состоянии система ни оказалась после (n-1)-го шага, будет известно, какое следует принять решение на n-м шаге. Известно также и соответствующее значение функции (2.4). Рассмотрим функциональное уравнение при k=n-2:
F2(X(n-1))=max[Wn-1(X(n-2), un-1)+F1(X(n-1))]. (2.5)
Un-1
Для того чтобы найти значения F2 для всех допустимых значений X(n-2), необходимо знать Wn-1(X(n-2), un-1) и F1(X(n-1)). Что касается значений F1(X(n-1)), то они уже определены.Поэтому нужно произвести вычисления для Wn-1(X(n-2), un-1) при некотором отборе допустимых значений X(n-2) и соответствующих управлений un-1 . Эти вычисления позволят определить условно оптимальное управление u0n-1 для каждого X(n-2) . Каждое из таких управлений совместно с уже выбранным управлением на последнем шаге обеспечивает максимальное значение дохода на двух последних шагах.
Последовательно осуществляя описанный выше итерационный процесс, дойдем до первого шага. На этом шаге известно, в каком состоянии может находиться система. Поэтому уже не требуется делать предположений о допустимых состояниях системы, а остается лишь только выбрать управление, которое является наилучшим с учетом условно оптимальных управлений, уже принятых на всех последующих шагах.
Таким образом, в результате последовательного прохождения всех этапов от конца к началу определяется максимальное значение выигрыша за n шагов и для каждого из них находим условно оптимальное управление.
Чтобы найти оптимальную стратегию управления, то есть определить искомое решение задачи, нужно теперь пройти всю последовательность шагов, только на этот раз от начала к концу. А именно: на первом шаге в качестве оптимального управления u1* возьмем найденное условно оптимальное управление u10. На втором шаге найдем состояние X1* , в которое переводит систему управление u1*. Это состояние определяет найденное условно оптимальное u20 , которое теперь считается оптимальным. Зная u2*, находим X2*, а значит, определяем u3* и т.д. В результате этого найдется решение задачи, то есть максимально возможный доход и оптимальную стратегию управления U*, включающую оптимальные управления на отдельных шагах: U*= (u1*, u2*, …, un*).
Итак, из нахождения решения задачи динамического программирования видно, что этот процесс является довольно громоздким. Поэтому более сложные задачи решают с помощью ЭВМ.[1].
Динамическую задачу по замене оборудования возможно также решить и графическим методом. На оси Х откладывают номер шага (к). на оси У – возраст оборудования (t). Точка (к-1;t) на плоскости соответствует началу К-ого шага по эксплуатации оборудования в возрасте t лет.
![]() Любая траектория переводящая точку S(k-1;t) из состояния S0 S, . Состоит из отрезков, то есть из шагов соответствующих годам эксплуатации. Нужно выбрать такую траекторию при которой затраты на эксплуатацию будут минимальны. Если известны зависимость производительности установленного на предприятии оборудования от времени его использования R(t) и зависимость затрат на ремонт оборудования при различном времени его использования S(t) и затраты связанные с приобретением нового оборудования, то показателем эффективности в этом случае является прибыль которая максимизируется.
Любая траектория переводящая точку S(k-1;t) из состояния S0 S, . Состоит из отрезков, то есть из шагов соответствующих годам эксплуатации. Нужно выбрать такую траекторию при которой затраты на эксплуатацию будут минимальны. Если известны зависимость производительности установленного на предприятии оборудования от времени его использования R(t) и зависимость затрат на ремонт оборудования при различном времени его использования S(t) и затраты связанные с приобретением нового оборудования, то показателем эффективности в этом случае является прибыль которая максимизируется.
Похожие работы
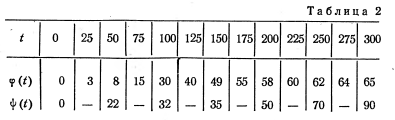
... . При t = 10= = = 7 (замена). Из табл.1 видно, что r(t) - λ(t) с ростом t убывает. Поэтому при t > 9 оптимальной будет политика замены оборудования. Чтобы различать, в результате какой политики получается условно-оптимальное значение прибыли, будем эти значения разграничивать (до t = 9 включительно оптимальной является политика сохранения). Для заполнения второй строки табл.1, используем ...
... параметрами, показателями объекта именно в то время. Дискретные модели отображают состояние объекта управления в отдельные, фиксированные моменты времени. Имитационными называют экономико-математические модели, используемые с целью имитации управляемых экономических объектов и процессов с применением средств информационной и вычислительной техники. По типу математического аппарата, применяемого в ...
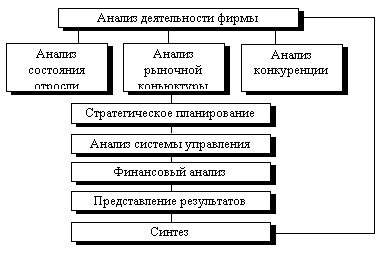
... контактов и связей. Основой такого подхода к резервам являются финансы. 2. Доступ к кредитам - выработка финансовой политики, управления активами и пассивами. 1.3 Этапы разработки внутрифирменного плана. Процесс стратегического планирования состоит из семи взаимосвязанных этапов; осуществляется совместно руководством фирмы и сотрудниками маркетинговых служб. Формирование стратегических ...
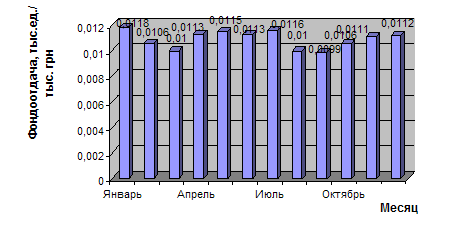
... ,9 тыс. грн. Найдём производную от валовых издержек, тогда имеем: ВИ’ (Vпр)=ПрИ(Vпр) =0,1119*(Vпр) – 5,6098*(Vпр) + 91,676, грн / ед. 2.3 Определение оптимального объёма производства Определим оптимальный объём производства: 1) аналитическими методами: Ⅰ Сравнение валовых издержек с валовым доходом. Из метода сравнения валовых издержек с валовым доходом имеем что, оптимальный ...
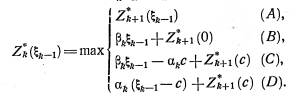




0 комментариев