Навигация
РАСЧЕТ ПОКАЗАТЕЛЕЙ ЭКОНОМИКО-МАТЕМАТИЧЕСКОЙ МОДЕЛИ И ЭКОНОМИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ РЕЗУЛЬТАТОВ
3. РАСЧЕТ ПОКАЗАТЕЛЕЙ ЭКОНОМИКО-МАТЕМАТИЧЕСКОЙ МОДЕЛИ И ЭКОНОМИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ РЕЗУЛЬТАТОВ
В этой задаче в качестве системы S выступает оборудование. Состояние этой системы определяются фактическим временем использования оборудования (его возрастом) t, то есть описываются единственным параметром t.
В качестве управлений выступают решения о замене и сохранении оборудования, принимаемые в начале каждого года. Обозначим через Xc решение о сохранении оборудования, а через Xз –решение о замене оборудования. Тогда задача состоит в нахождении такой стратегии управления, определяемой решениями, принимаемыми к началу каждого года, при которой общая прибыль предприятия за восемь лет является максимальной.
Эта задача обладает свойствами аддитивности и отсутствия последействия. Следовательно, ее решение можно найти с помощью алгоритма, реализуемого в два этапа. На первом этапе при движении от начала 10-го года периода к началу 1-го года для каждого допустимого состояния оборудования найдем условное оптимальное управление (решение), а на втором этапе при движении от начала 1-го года периода к началу 10-года из условных оптимальных решений для каждого года составим оптимальный план замены оборудования на десять лет.
Для определения условных оптимальных решений сначала необходимо составить функциональное уравнение Беллмана. Так как было предположено, что к началу k-го года (k=1,2,3,4,5,6,7,8,9,10) может приниматься только одно из двух решений – заменять или не заменять оборудование, то прибыль предприятия за k-ый год составит:
![]() Z*k = max r(t)-s(t)+Zk+1(t+1) ; Xc
Z*k = max r(t)-s(t)+Zk+1(t+1) ; Xc
r(0)-s(0)-P0+Zk+1(1) ;Xз (3.1)
где t –возраст оборудования к началу k-го года (k=1,2,3,4,5,6,7,8,9,10); Xk –управление, реализуемое к началу k-го года; P0 –стоимость нового оборудования.
Используя теперь уравнение (3.1) , находим решение исходной задачи. Это решение начинается с определения условно оптимального управления (решения) для последнего (10-го) года периода, в связи с чем находим множество допустимых состояний оборудования к началу данного года. Так как к началу периода имеется новое оборудование (t =0), то возраст оборудования к началу 10-го года может составлять 1,2,3,4,5,6,7,8,9 лет. Для каждого из этих состояний найдем условно оптимальное решение и соответствующее значение функции Z*10(t).
 Z*10(1)=max
8,99 = 8,99; Xc
Z*10(1)=max
8,99 = 8,99; Xc
-0,07
 Z*10(2)=max
8,06 = 8,06; Xc
Z*10(2)=max
8,06 = 8,06; Xc
-0,07
 Z*10(3)=max
6,89 = 6,89; Xc
Z*10(3)=max
6,89 = 6,89; Xc
-0,07
 Z*10(4)=max
6,07 = 6,07; Xc
Z*10(4)=max
6,07 = 6,07; Xc
-0,07
 Z*10(5)=max
6,14 = 6,14; Xc
Z*10(5)=max
6,14 = 6,14; Xc
-0,07
 Z*10(6)=max
4,04 = 4,04; Xc
Z*10(6)=max
4,04 = 4,04; Xc
-0,07
 Z*10(7)=max
3,00 = 3,00; Xc
Z*10(7)=max
3,00 = 3,00; Xc
-0,07
 Z*10(8)=max
0,89 = 0,89; Xc
Z*10(8)=max
0,89 = 0,89; Xc
-0,07
 Z*10(9)=max 0,14 = 0,14; Xc
Z*10(9)=max 0,14 = 0,14; Xc
-0,07
Полученные результаты сведены в таблицу 3.1
Таблица 3.1
Возможное состояние оборудование к началу 10-го года периода
| Возраст оборудования t (лет) | Значения функции Z*10(t) (тыс.д.ед.) | Условно оптимальное решение Х |
| 1 | 8,99 | Xc |
| 2 | 8,06 | Xc |
| 3 | 6,89 | Xc |
| 4 | 6,07 | Xc |
| 5 | 6,14 | Xc |
| 6 | 4,04 | Xс |
| 7 | 3 | Xс |
| 8 | 0,89 | Xс |
| 9 | 0,14 | Xс |
Рассмотрим возможное состояние оборудование к началу 9-го года периода и найдем соответствующие значения функции Z*9(t).
 Z*9(1)=max 17,05 = 17,05; Xc
Z*9(1)=max 17,05 = 17,05; Xc
8,92
 Z*9(2)=max
14,95 = 14,95; Xc
Z*9(2)=max
14,95 = 14,95; Xc
8,92
 Z*9(3)=max 12,96 = 12,96; Xc
Z*9(3)=max 12,96 = 12,96; Xc
8,92
 Z*9(4)=max
12,21 = 12,21; Xc
Z*9(4)=max
12,21 = 12,21; Xc
8,92
 Z*9(5)=max
10,18 = 10,18; Xc
Z*9(5)=max
10,18 = 10,18; Xc
8,92
 Z*9(6)=max
7,04 = 8,92; Xc
Z*9(6)=max
7,04 = 8,92; Xc
8,92
 Z*9(7)=max 3,89 = 8,92; Xc
Z*9(7)=max 3,89 = 8,92; Xc
8,92
 Z*9(8)=max
4,04 = 8,92; Xc
Z*9(8)=max
4,04 = 8,92; Xc
8,92
Полученные результаты записаны в таблице 3.2
Таблица 3.2
возможное состояние оборудование к началу 9-го года периода
| Возраст оборудования t (лет) | Значения функции Z*9(t) (тыс.д.ед.) | Условно оптимальное решение Х |
| 1 | 17,05 | Xc |
| 2 | 14,95 | Xc |
| 3 | 12,96 | Xс |
| 4 | 12,21 | Xс |
| 5 | 10,18 | Xс |
| 6 | 8,92 | Xз |
| 7 | 8,92 | Xз |
| 8 | 8,92 | Xз |
Определим условно оптимальное решение для каждого из допустимых состояний оборудования к началу 8-го года периода.
В соответствии с уравнением 3.1 имеем:
 Z*8(1)=max23,94 = 23,94 ; Xc
Z*8(1)=max23,94 = 23,94 ; Xc
 16,98
16,98
Z*8(2)=max21,02 = 21,02 ; Xc
16,98
 Z*8(3)=max19,10 = 19,10 ; Xc
Z*8(3)=max19,10 = 19,10 ; Xc
16,98
 Z*8(4)=max16,25 = 16,98 ; Xз
Z*8(4)=max16,25 = 16,98 ; Xз
16,98
 Z*8(5)=max 15,06= 16,98 ; Xз
Z*8(5)=max 15,06= 16,98 ; Xз
16,98

Z*8(6) =max 12,96 =16,98 ; Xз
 16,98
16,98
Z*8(7)=max16,98 = 16,98 ; Xз,Xс
16,98
Полученные результаты сведены в таблицу 3.3
Таблица 3.3
Возможное состояние оборудование к началу 8-го года периода
| Возраст оборудования t (лет) | Значения функции Z*8(t) (тыс.д.ед.) | Условно оптимальное решение Х |
| 1 | 23,94 | Xc |
| 2 | 21,02 | Xc |
| 3 | 19,10 | Xc |
| 4 | 16,98 | Xз |
| 5 | 16,98 | Xз |
| 6 | 16,98 | Xз |
| 7 | 16,98 | Xc,Xз |
Рассмотрим возможное состояние оборудование к началу 7-го года периода и найдем соответствующие значения функции Z*7(t).
 Z*7(1)=max 8,99 +21,02 = 30,01 ; Xc
Z*7(1)=max 8,99 +21,02 = 30,01 ; Xc
 9,93-10+23,94
9,93-10+23,94
Z*7(2)=max 8,06+19,10 = 27,16 ; Xc
 23,87
23,87
Z*7(3)=max 6,89+16,98 = 23,87 ; Xз ,Xс
23,87
 Z*7(4)=max
6,07+16,98 = 23,87 ; Xз
Z*7(4)=max
6,07+16,98 = 23,87 ; Xз
23,87
 Z*7(5)=max
6,14+16,98 = 23,87 ; Xз
Z*7(5)=max
6,14+16,98 = 23,87 ; Xз
23,87

Z*7(6)=max 4,04+16,98 = 23,87 ; Xз
23,87
Полученные результаты записаны в таблице 3.4
Таблица 3.4
возможное состояние оборудование к началу 7-го года периода
| Возраст оборудования t (лет) | Значения функции Z*7(t) (тыс.д.ед.) | Условно оптимальное решение Х |
| 1 | 30,01 | Xc |
| 2 | 27,16 | Xc |
| 3 | 23,87 | Xз,Xс |
| 4 | 23,87 | Xз |
| 5 | 23,87 | Xз |
| 6 | 23,87 | Xз |
Определим условно оптимальное решение для каждого из допустимых состояний оборудования к началу 6-го года периода.
В соответствии с уравнением 3.1 имеем:

Z*6(1)=max 8,99+ 27,16 = 36,15 ; Xc
29,94

Z*6(2)=max 8,06+23,87 = 31,93 ; Xc
29,94

Z*6(3)=max 6,89+23,87 = 30,76 ; Xс
29,94
 Z*6(4)=max 6,07+23,87 = 29,94 ; Xз , Xс
Z*6(4)=max 6,07+23,87 = 29,94 ; Xз , Xс
29,94

Z*6(5)=max 6,14+23,87 = 30,01 ; Xс
29,94
Из значения функции Z*6(4) видно, что если к началу 6-го года периода возраст оборудования составляет 4 года, то независимо от того, будет ли принято решение Xc или Xз, величина прибыли окажется одной и той же. Это означает, что в качестве условно оптимального решения можно взять любое. Полученные значения для Z*6(t) записаны в таблице 3.5
Таблица 3.5
возможное состояние оборудование к началу 6-го года периода
| Возраст оборудования t (лет) | Значения функции Z*6(t) (тыс.д.ед.) | Условно оптимальное решение Х |
| 1 | 36,15 | Xc |
| 2 | 31,93 | Xc |
| 3 | 30,76 | Xс |
| 4 | 29,94 | Xс,Xз |
| 5 | 30,01 | Xс |
Рассмотрим возможное состояние оборудования к началу 5-го года и найдем для каждого из них условно оптимальное решение и соответствующее значение функции Z*5(t).
 Z*5(1)=max 8,99+31,93 = 40,92 ; Xc
Z*5(1)=max 8,99+31,93 = 40,92 ; Xc
36,08
 Z*5(2)=max 8,06+30,76 = 38,82 ; Xc
Z*5(2)=max 8,06+30,76 = 38,82 ; Xc
36,08
 Z*5(3)=max 6,89+29,94 = 36,83 ; Xс
Z*5(3)=max 6,89+29,94 = 36,83 ; Xс
36,08
 Z*5(4)=max 6,07+30,01 = 36,08 ; Xз ,Xс
Z*5(4)=max 6,07+30,01 = 36,08 ; Xз ,Xс
36,08
Полученные результаты записаны в таблице 3.6.
Таблица 3.6
возможное состояние оборудование к началу 5-го года периода
| Возраст оборудования t (лет) | Значения функции Z*5(t) (тыс.д.ед.) | Условно оптимальное решение Х |
| 1 | 40,92 | Xc |
| 2 | 38,82 | Xc |
| 3 | 36,83 | Xс |
| 4 | 36,08 | Xс,Xз |
Определим условно оптимальное решение для каждого из допустимых состояний оборудования к началу 4-го года периода. В соответствии с уравнением (3.1):
 Z*4(1)=max 8,99+38,82 = 47,81 ; Xc
Z*4(1)=max 8,99+38,82 = 47,81 ; Xc
40,85
 Z*4(2)=max 8,06+ 36,83 = 44,89 ; Xc
Z*4(2)=max 8,06+ 36,83 = 44,89 ; Xc
40,85
 Z*4(3)=max 6,89+36,08 = 42,97 ; Xс
Z*4(3)=max 6,89+36,08 = 42,97 ; Xс
40,85
Полученные результаты записаны в таблице 3.7.
Таблица 3.7
возможное состояние оборудование к началу 4-го года периода
| Возраст оборудования t (лет) | Значения функции Z*4(t) (тыс.д.ед.) | Условно оптимальное решение Х |
| 1 | 47,81 | Xc |
| 2 | 44,89 | Xc |
| 3 | 42,97 | Xс |
Рассмотрим возможное состояние оборудования к началу 3-го года и найдем для каждого из них условно оптимальное решение и соответствующее значение функции Z*3(t).

Z*3(1)=max 8,99+44,89 = 53,88 ; Xc
47,74
 Z*3(2)=max 8,06+42,97 = 51,03 ; Xc
Z*3(2)=max 8,06+42,97 = 51,03 ; Xc
47,74
Полученные результаты записаны в таблице 3.8.
Таблица 3.8
Возможное состояние оборудование к началу 3-го года периода
| Возраст оборудования t (лет) | Значения функции Z*3(t) (тыс.д.ед.) | Условно оптимальное решение Х |
| 1 | 53,88 | Xc |
| 2 | 51,03 | Xc |
Теперь рассматриваются допустимые состояния оборудования к началу 2-го года периода. На данный момент времени возраст оборудования может быть равен только лишь одному году. Поэтому предстоит сравнить лишь два возможных решения: сохранить оборудование или произвести замену.
 Z*2(1)=max 8,99+51,03 = 60,02 ; Xc
Z*2(1)=max 8,99+51,03 = 60,02 ; Xc
53,81
К началу второго года периода оборудование требуется сохранить.
Согласно условию к началу периода установлено новое оборудование (t=0). Поэтому проблема выбора между сохранением и заменой оборудования не существует: оборудование следует сохранить. Значит, условно оптимальным решением является Xc, а значение функции: Z*1(1)=9,93+60,02 =69,95.
Таким образом, максимальная прибыль предприятия может быть равной 69,95 тыс.д.ед. Она соответствует оптимальным планам замены оборудования, т.к. оптимальный план не единственный. Оптимальные планы получаются на основе данных таблиц 3.1, 3.2, 3.3, 3.4, 3.5, 3.6, 3.7, 3.8, то есть в результате вычислительного процесса, состоящего в прохождении всех рассмотренных шагов с начала 1-го до начала 10-го года периода. Для 1-го года периода решение единственно – следует сохранить оборудование. Значит возраст оборудования к началу 2-го года периода равен одному году. Тогда оптимальным решением для 2-го года периода является решение о сохранении оборудования. Реализация такого решения приводит к тому, что возраст оборудования к началу 3-го года периода становится равным двум годам. При таком возрасте (см. табл.3.8) оборудование в 3-м году периода следует сохранить. После сохранения оборудования его возраст к началу 4-го года периода составит три года. Как видно из таблицы 3.7 , при таком возрасте оборудование следует сохранить. Поэтому возраст оборудования к началу 5-го года периода составит четыре года. Из таблицы 3.6 следует, что оборудование следует сохранить или заменить и в случае сохранения его возраст к началу 6-го периода составит пять лет, и оборудование вновь следует сохранить (см. таблицу 3.5). Если мы оборудование сохраняем к началу 7-го года периода, то возраст оборудования будет шесть лет, а из таблицы 3.4 следует, что оборудование следует заменить. К началу 8-го года периода возраст оборудования составит один год, а это значит, оборудование следует сохранить (см. таблицу 3.3). К началу 9-го года периода возраст оборудования составит два года и в соответствие с таблицей 3.2 оно опять сохраняется. К началу 10-го года периода оборудование сохраняется (см. таблицу 3.1).
Рассмотрим следующий оптимальный план:
Для этого вернемся к началу 5-го года периода, когда возраст оборудования будет равным четырём годам. При таком возрасте (см. табл.3.6) оборудование в 5-м году периода следует сохранить или заменить. В отличие от предыдущего оптимального плана, заменим оборудование. После замены оборудования его возраст к началу 6-го года периода составит один год. Как видно из таблицы 3.5, при таком возрасте оборудование следует сохранить. Поэтому возраст оборудования к началу 7-го года периода составит два года. Из таблицы 3.4 следует, что оборудование следует сохранить и его возраст составит три года, значит, к началу 8-го года оборудование следует сохранить (см. таблицу 3.3). Если мы оборудование сохраняем к началу 9-го года периода, то возраст оборудования будет четыре года, а из таблицы 3.2 следует, что оборудование следует сохранить. К началу 10-го года периода возраст оборудования составит пять лет, а это значит, оборудование следует сохранить (см. таблицу 3.1).
Таблица 3.9
Оптимальные планы замены оборудования
| Возраст оборудования t | Оптимальные планы | |
| I | II | |
| 1 | Сохранить | |
| 2 | Сохранить | |
| 3 | Сохранить | |
| 4 | Сохранить | |
| 5 | Сохранить | Заменить |
| 6 | Сохранить | |
| 7 | Заменить | Сохранить |
| 8 | Сохранить | |
| 9 | Сохранить | |
| 10 | Сохранить | |
Запишем в таблицу 3.9 данные нашей задачи, и на основании этой таблицы построим график зависимости производительности оборудования от времени его использования предприятием.
Таблица 3.10
Данные задачи замены оборудования
| Годы эксплуатации | Затраты S(t) | Годовая продукция r(t) | r(t)-S(t) | |||
| 0 | 15,07 | 25 | 9,93 | |||
| 1 | 15,01 | 24 | 8,99 | |||
| 2 | 15,94 | 24 | 8,06 | |||
| 3 | 16,11 | 23 | 6,89 | |||
| 4 | 16,93 | 23 | 6,07 | |||
| 5 | 16,86 | 23 | 6,14 | |||
| 6 | 17,96 | 22 | 4,04 | |||
| 7 | 18 | 21 | 3 | |||
| 8 | 19,11 | 20 | 0,89 | |||
| 9 | 19,86 | 20 | 0,14 | |||
10 | 20,18 | 20 | -0,18 |
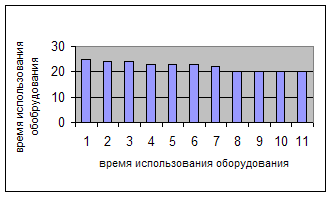
Зависимость производительности оборудования от времени его использования предприятием
Рис.3.1
Из графика видно, что производительность оборудования со временем падает, то есть оборудование стареет и требует ремонта или замены.
В таблице 3.10 сведены значения оптимальных планов замены оборудования.
Таблица 3.10
Значения оптимальных планов замены оборудования
| I | II |
| 69,95 | 69,95 |
| 60,02 | 60,02 |
| 51,03 | 51,03 |
| 42,97 | 42,97 |
| 36,08 | 36,08 |
| 30,01 | 36,15 |
| 23,87 | 27,16 |
| 23,94 | 19,10 |
| 14,95 | 12,21 |
| 6,89 | 6,14 |
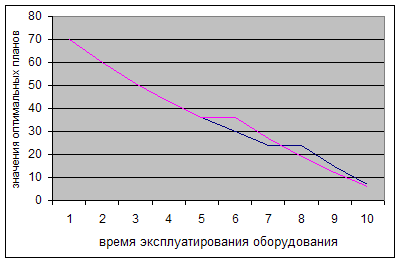
Зависимость получаемой прибыли предприятием от времени использования эксплуатируемого оборудования при оптимальных планах его замены
Рис.3.2
На рисунке 3.2 изображено два оптимальных плана. Из рисунка видно, что к началу 5-го года значения всех оптимальных планов одинаковы.
ЗАКЛЮЧЕНИЕ
Динамическое программирование – это область математического программирования, включающая совокупность приемов и средств для нахождения оптимального решения, а также оптимизации каждого шага в системе и выработке стратегии управления, то есть процесс управления можно представить как многошаговый процесс. Динамическое программирование, используя поэтапное планирование, позволяет не только упростить решение задачи, но и решить те из них, к которым нельзя применить методы математического анализа. Упрощение решения достигается за счет значительного уменьшения количества исследуемых вариантов, так как вместо того, чтобы один раз решать сложную многовариантную задачу, метод поэтапного планирования предполагает многократное решение относительно простых задач. Планируя поэтапный процесс, исходят из интересов всего процесса в целом, т.е. при принятии решения на отдельном этапе всегда необходимо иметь в виду конечную цель.
Однако динамическое программирование имеет и свои недостатки. В отличие от линейного программирования, в котором симплексный метод является универсальным, в динамическом программировании такого метода не существует. Каждая задача имеет свои трудности, и в каждом случае необходимо найти наиболее подходящую методику решения. Недостаток динамического программирования заключается также в трудоемкости решения многомерных задач. Задача динамического программирования должна удовлетворять два условия. Первое условие обычно называют условием отсутствия последействия, а второе –условием аддитивности целевой функции задачи.
На практике встречаются такие задачи планирования, в которых заметную роль играют случайные факторы, влияющие как на состояние системы, так и на выигрыш. Существует разница между детерминированной и стохастической задачами динамического программирования. В детерминированной задаче оптимальное управление является единственным и указывается заранее как жесткая программа действий. В стохастической задаче оптимальное управление является случайным и выбирается в ходе самого процесса в зависимости от случайно сложившейся ситуации. В детерминированной схеме, проходя процесс по этапам от конца к началу, тоже находится на каждом этапе целый ряд условных оптимальных управлений, но из всех этих управлений, в конечном счете осуществлялось только одно. В стохастической схеме это не так. Каждое из условных оптимальных управлений может оказаться фактически осуществленным, если предшествующий ход случайного процесса приведет систему в соответствующее состояние.
Принцип оптимальности является основой поэтапного решения задач динамического программирования. Типичными представителями экономических задач динамического программирования являются так называемые задачи производства и хранения, задачи распределения капиталовложений, задачи календарного производственного планирования и другие. Задачи динамического программирования применяются в планировании деятельности предприятия с учетом изменения потребности в продукции во времени. В оптимальном распределении ресурсов между предприятиями в направлении или во времени.
Описание характеристик динамического программирования и типов задач, которые могут быть сформулированы в его рамках, по необходимости должно быть очень общим и несколько неопределенным, так как существует необозримое множество различных задач, укладывающихся в схему динамического программирования. Только изучение большого числа примеров дает отчетливое понимание структуры динамического программирования.
СПИСОК ЛИТЕРАТУРЫ
1.Акулич И.Л. Математическое программирование в примерах и задачах.- М.: Высшая школа, 1993.
2.Вентцель Е.С. Элементы динамического программирования.- М.: Наука, 1964.
3. Дудорин В.И. Моделирование в задачах управления производством.-М.: Статистика, 1980.
4. Исследования операций в экономике: учебное пособие для ВУЗов / под ред. Кремера Н.Ш. –М.: Банки и Биржи , ЮНИТИ, 1997.
5. Карасев А.И., Кремер Н.Ш., Савельева Т.И. Математические методы и модели в планировании.-М.: Экономика, 1987.
6. Карманов В.Г. Математическое программирование. –М.: Наука, 1986.
7.Колемаев В.А. Математическая экономика.- М.: Юнити,1998.
8. Лотов А.В. введение в экономико-математическое моделирование.-М.: Наука, 1984.
9. Ромакин М.И. Оптимизация планирования производства: экономико-математические модели и методы.-М.: Финансы и статистика, 1981.
10. Таха Х.А. Введение в исследование операций. Кн.1 и2.-М.:Мир, 1985.
11. Терехов Л.Л. Экономико-математические методы.- М.: Статистика, 1972.
12. Фатхутдинов Р.А. Разработка управленческого решения. Учебное пособие.-М.:Интер-Синтез, 1997.
13. Фатхутдинов Р.А. Система менеджмента.-М.: Интер-Синтез, 1996.
14. Хедли Дж. Нелинейное и динамическое программирование.- М.: Мир, 1967.
ПРИЛОЖЕНИЯ
Приложение 1
Таблица 1.1
Затраты на содержание и ремонт аналогичного оборудования других предприятий
| Порядковые годы эксплу-атации оборудования | Показатели | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | Затраты, тыс. д.ед. | 14,7-14,9 | 14,9-15,1 | 15,1-15,3 | 15,3-15,5 | 15,5 и более |
| Коли-чество пред-приятий | 4 | 5 | 2 | 2 | 1 | |
| 1 | Затраты, тыс. д.ед. | 14,6-14,8 | 14,8-15,0 | 15,0-15,2 | 15,2-15,4 | 15,4 и более |
| Коли-чество пред-приятий | 3 | 4 | 4 | 2 | 1 | |
| 2 | Затраты, тыс. д.ед. | 15,4-15,6 | 15,6-15,8 | 15,8-16,0 | 16,0-16,2 | 16,2 и более |
| Коли-чество пред-приятий | 2 | 3 | 2 | 4 | 3 | |
| 3 | Затраты, тыс. д.ед. | До 15 | 15,5-16,0 | 16,0-16,5 | 16,5-17,0 | 17,0 и более |
| Коли-чество пред-приятий | 3 | 4 | 3 | 2 | 2 | |
| 4 | Затраты, тыс. д.ед. | 16,5-16,7 | 16,7-16,9 | 16,9-17,1 | 17,1 и более | |
| Коли-чество пред-приятий | 3 | 3 | 4 | 4 | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 5 | Затраты, тыс. д.ед. | До 16,0 | 16,0-16,5 | 16,5-17,0 | 17,-17,5 | 17,5 и более |
| Коли-чество пред-приятий | 2 | 2 | 4 | 3 | 3 | |
| 6 | Затраты, тыс. д.ед. | 17,5-17,7 | 17,7-17,9 | 17,9-18,1 | 18,1-18,3 | 18,3 и более |
| Коли-чество пред-приятий | 3 | 3 | 4 | 2 | 2 | |
| 7 | Затраты, тыс. д.ед. | До17,8 | 17,8-18,0 | 18,0-18,2 | 18,2 и более | |
| Коли-чество пред-приятий | 3 | 4 | 4 | 3 | ||
| 8 | Затраты, тыс. д.ед. | 18,0-18,5 | 18,5-19,0 | 19,0-19,5 | 19,5-20,0 | 20,0 и более |
| Коли-чество пред-приятий | 3 | 4 | 3 | 2 | 2 | |
Похожие работы
... . При t = 10= = = 7 (замена). Из табл.1 видно, что r(t) - λ(t) с ростом t убывает. Поэтому при t > 9 оптимальной будет политика замены оборудования. Чтобы различать, в результате какой политики получается условно-оптимальное значение прибыли, будем эти значения разграничивать (до t = 9 включительно оптимальной является политика сохранения). Для заполнения второй строки табл.1, используем ...
... параметрами, показателями объекта именно в то время. Дискретные модели отображают состояние объекта управления в отдельные, фиксированные моменты времени. Имитационными называют экономико-математические модели, используемые с целью имитации управляемых экономических объектов и процессов с применением средств информационной и вычислительной техники. По типу математического аппарата, применяемого в ...
... контактов и связей. Основой такого подхода к резервам являются финансы. 2. Доступ к кредитам - выработка финансовой политики, управления активами и пассивами. 1.3 Этапы разработки внутрифирменного плана. Процесс стратегического планирования состоит из семи взаимосвязанных этапов; осуществляется совместно руководством фирмы и сотрудниками маркетинговых служб. Формирование стратегических ...
... ,9 тыс. грн. Найдём производную от валовых издержек, тогда имеем: ВИ’ (Vпр)=ПрИ(Vпр) =0,1119*(Vпр) – 5,6098*(Vпр) + 91,676, грн / ед. 2.3 Определение оптимального объёма производства Определим оптимальный объём производства: 1) аналитическими методами: Ⅰ Сравнение валовых издержек с валовым доходом. Из метода сравнения валовых издержек с валовым доходом имеем что, оптимальный ...
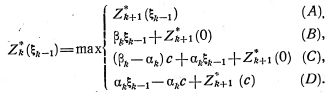
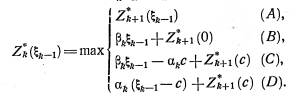




0 комментариев