Навигация
Классификация и принципы построения математических моделей
2. Классификация и принципы построения математических моделей
Можно выделить следующие основные этапы построения математической модели:
Определение цели, т.e. чего хотят добиться, решая поставленную задачу.
Определение пapaметров модели, т.е. заранее известных фиксированных факторов, на значения которых исследователь не влияет.
Формирование управляющих переменных, изменяя значение которых можно приближаться к поставленной цели. Значения управляющих переменных являются решениями задачи.
Определение области допустимых решений, т.е. тех ограничений, которым должны удовлетворять управляющие переменные.
Выявление неизвестных факторов, т.е. величин, которые могут изменяться случайным или неопределенным образом.
Выражение цели через управляющие переменные, параметры и неизвестные факторы, т.e. формирование целевой функции, называемой также критерием эффективности или критерием оптимальности задачи.
Введем следующие условные обозначения:
- параметры модели;
x - управляющие переменные или решения;
X - область допустимых решений;
- случайные или неопределенные факторы;
W - целевая функция или критерий эффективности (критерий оптимальности).
W=W (x, , )
В соответствии с введенными терминами, математическая модель задачи имеет следующий вид:
W=W (x, , ) max (min) (2.1)
x X
Решить задачу - это значит найти такое оптимальное решение xX, чтобы при данных фиксированных параметрах и с учетом неизвестных факторов значения критерия эффективности W было по возможности максимальным (минимальным).
W=W (x, , ) = max (min) W (x, , )
x X
Таким образом, оптимальное решение - это решение, предпочтительное перед другими по определенному критерию эффективности (одному или нескольким).
Перечислим некоторые основные принципы построения математической модели:
Необходимо соизмерять точность и подробность модели, во-первых, с точностью тex исходных данных, которыми располагает исследователь, и, во-вторых, с теми результатами, которые требуется получить.
Математическая модель должна отражать существенные черты исследуемого явления и при этом не должна его сильно упрощать.
Математическая модель не может быть полностью адекватна реальному явлению, поэтому для его исследования лучше использовать несколько моделей, для построения которых применены разные математические методы. Если при этом получаются сходные результаты, то исследование заканчивается. Если результаты сильно различаются, то следует пересмотреть постановку задачи.
Любая сложная система всегда подвергается малым внешним и внутренним воздействиям, следовательно, математическая модель должна быть устойчивой (сохранять свойства и структуру при этих воздействиях).
По числу критериев эффективности математические модели делятся на однокритериальные и многокритериальные. Многокритериальные математические модели содержат два и более критерия.
По учету неизвестных факторов математические модели делятся на детерминированные, стохастические и модели с элементами неопределенности.
В стохастических моделях неизвестные факторы - это случайные величины, для которых известны функции распределения и различные статистические характеристики (математическое ожидание, дисперсия, среднеквадратическое отклонение и т.п.). Среди стохастических характеристик можно выделить:
- модели стохастического программирования, в которых либо в целевую функцию (2.1), либо в ограничения (2.2) входят случайные величины;
- модели теории случайных процессов, предназначенные для изучения процессов, состояние которых в каждый момент времени является случайной величиной;
- модели теории массового обслуживания, в которой изучаются многоканальные системы, занятые обслуживанием требований. Также - к стохастическим моделям можно отнести модели теории полезности, поиска и принятия решений.
Для моделирования ситуаций, зависящих от факторов, для которых невозможно собрать статистические данные и значения которых не определены, используются модели с элементами неопределенности.
В моделях теории игр задача представляется в виде игры, в которой участвуют несколько игроков, преследующих разные цели, например, организацию предприятия в условиях конкуренции.
В имитационных моделях реальный процесс разворачивается в машинном времени, и прослеживаются результаты случайных воздействии на него, например, организация производственного процесса.
В детерминированных моделях неизвестные факторы не учитываются. Несмотря на кажущуюся простоту этих моделей, к ним сводятся многие практические задачи, в том числе большинство экономических задач. По виду целевой функции и ограничений детерминированные модели делятся на: линейные, нелинейные, динамические и графические.
В линейных моделях целевая функция и ограничения линейны по управляющим переменным. Построение и расчет линейных моделей являются наиболее развитым разделом математического моделирования, поэтому часто к ним стараются свести и другие задачи либо на этапе постановки, либо в процессе решения. Для линейных моделей любого вида и достаточно большой размерности известны стандартные методы решения.
Hелинейные модели - это модели, в которых либо целевая функция, либо какое-нибудь из ограничений (либо все ограничения) нелинейны по управляющим переменным. Для нелинейных моделей нет единого метода расчета. В зависимости от вида нелинейности, свойств функции и ограничений можно предложить различные способы решения. Однако может случится и так, что для поставленной нелинейной задачи вообще не существует метода расчета. В этом случае задачу следует упростить, либо сведя ее к известным линейным моделям, либо просто линеаризовав модель.
В динамических моделях, в отличие от статических линейных и нелинейных моделей, учитывается фактор времени. Критерий оптимальности в динамических моделях может быть самого общего вида (и даже вообще не быть функцией), однако для него должны выполняться определенные свойства. Расчет динамических моделей сложен, и для каждой конкретной задачи необходимо разрабатывать специальный алгоритм решения.
Графические модели - используются тогда, когда задачу удобно представить в виде графической структуры.
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://www.monax.ru
Похожие работы
... лишь прагматическими представителями значительно более широкого перечня алгоритмов, применяющихся в планировании и других экономических расчетах. IV. Заключение Как видно из всего вышесказанного, значение математических моделей и информатики в управлении велико. В ближайшие 10 лет мир изменится сильнее, чем за предыдущие 50. И от того, насколько правильно мы сможем организовать свою жизнь, ...
... ситуации является определяющим фактором [7]. В зависимости от того, какой метод анализа модели выбран, факторныe разложения могут различаться. Глава 2. Применение детерминированных экономико-математических моделей и методов факторного анализа на примере РУП «ГЗЛиН». 2.1 Характеристика РУП «ГЗЛиН» 9 октября 1979 - издан приказ М 272 Министерства машиностроения для животноводства и ...
... и качественные характеристики этого элемента представлены ниже в таблице 1 за временной период с мая 2005 по май 2006. Для построения экономико-математической модели применен метод математической статистики. Расчеты по модели и анализ полученных результатов при использовании данного метода включает в себя этапы: 1.Графическое представление характеристик. 2.Предварительный статистический ...
... поколений. Естественно, особенно они заметны, если популяция находится в изоляции, т.е. отсутствует миграция генов извне. Известны сообщества такого рода в человеческом обществе. Часть 2 Математические модели нейронных систем Изучение нейронных систем -одно из самых романтических направлений научных исследований, поскольку нейронные системы присущи как человеку, так и животным. Самая ...
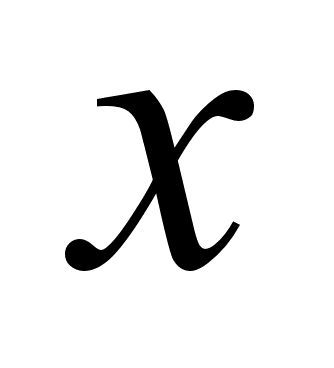
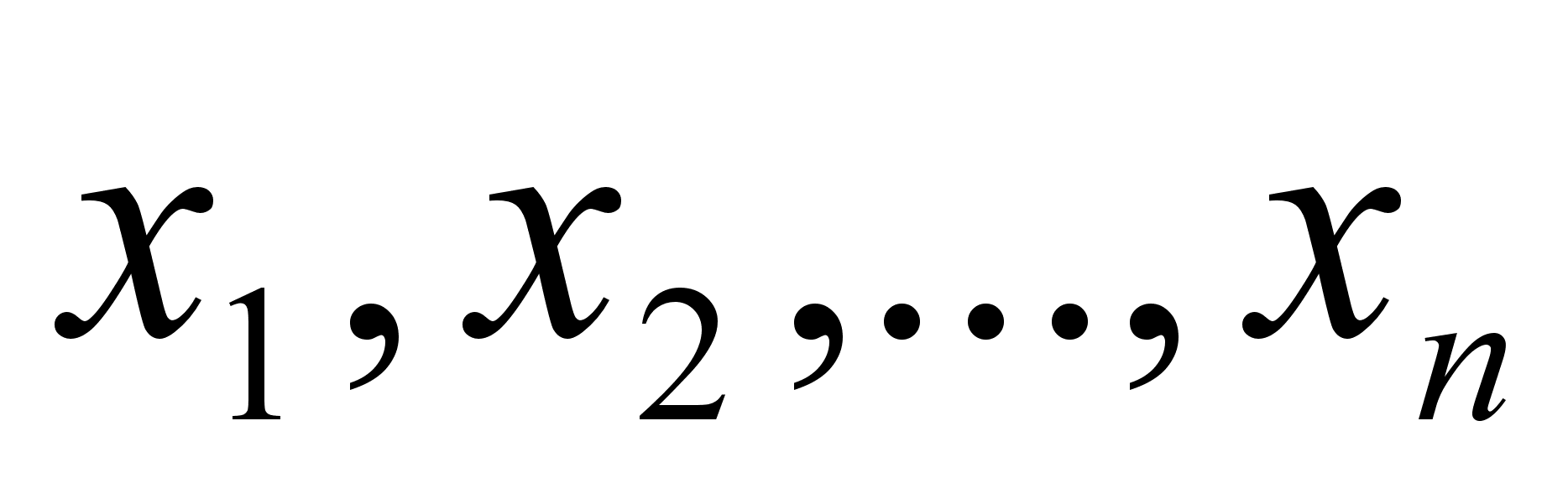
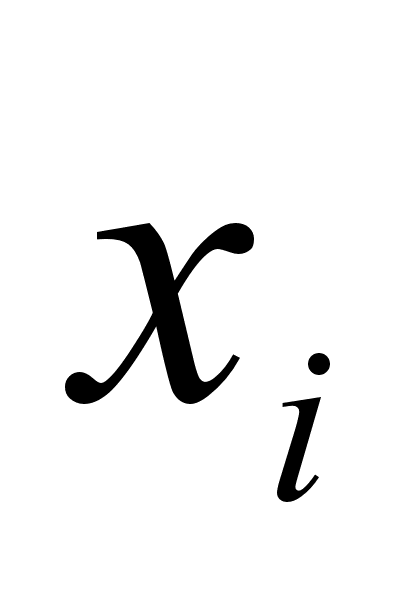

0 комментариев