Навигация
5.2. Пространство
Для изучения вопроса о пространстве вернемся к вопросу о его размерности. В начале статьи в ходе рассуждений мы пришли к выводу, что наше пространство должно обладать свойствами жидкости или газа, а материя представляет собой возмущения этой жидкости. Теперь обратимся к вопросу меры пространства, иными словами, каким образом мы оказались в трехмерном мире. Чисто феноменологически, нет оснований считать, что нет четвертого, пятого или какого-то еще измерения. Но тогда возникает вопрос о выделенности нашего трехмерного мира. То есть, если бы существовало измерение выше третьего, то мы могли бы наблюдать несоблюдение законов сохранения, но многолетней историей доказано обратное, по крайней мере в пределах доступных нам масштабов длин и времени.
Единственное, чем можно объяснить в рассматриваемой нами модели, выделенность трехмерного мира - это наличие границы раздела многомерной, конкретно 4-мерной, жидкости. Поэтому попробуем изучить некоторые поверхностные явления в такой жидкости. Для начала, чтобы получить наглядное представление о их,
рассмотрим некоторые поверхностные явления в трехмерной несжимаемой жидкости.
Самым характерным явлением в жидкости, как известно, являются вихри. В качестве системы координат возьмем поверхность жидкости, а третью координату будем считать нормалью к поверхности. То обстоятельство, что мы рассматриваем поверхностные явления, выражается в том, что третья координата представлена чисто мнимой.
Тогда запишем выражение вихря в жидкости. Условимся обозначать операции по действительным координатам символами κ, μ и λ, а символом ,3 и i,3 - если операция производится над 3-действительным и 4-комплексным векторами соответственно. Для общего случая n комплексных и m действительных осей комплексного пространства, обозначение будет выглядеть как ni,m.
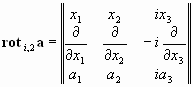
Псевдотензор вихря, как известно [4], запишется
![]()
Или в развернутой записи
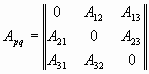
Рассмотрим каждую компоненту в отдельности. Из (2) можно получить выражение для dx
![]() (40)
(40)
Граничное условие на поверхности раздела выразится в том, что распространение “звука” должно происходить внутрь жидкости, таким образом, из (41) получим
![]() (41)
(41)
Тогда, следуя тем же рассуждениям, что и в [4], можно записать
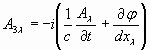
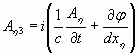
Где ![]() . Или, вводя новые обозначения
. Или, вводя новые обозначения
![]()
![]()
![]()
Окончательно, в таких обозначениях тензор поверхностного вихря запишется как
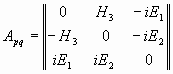
В случае 4-х мерной жидкости, рассуждения будут аналогичны и мы придем к выражению для тензора электромагнитного поля. Здесь не приведены эти выкладки, так как это известное выражение, к тому же все они аналогичны 3-х мерному случаю, в частности в [4], [6] приведены подробные выкладки. Просто запишем готовый результат
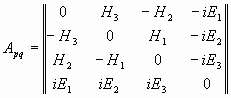 (42)
(42)
Окончательно, теперь запишем (42) в векторных обозначениях
![]() (43)
(43)
соответственно
![]() (44)
(44)
![]() (45)
(45)
Важно, что мы выполнили замену мнимой пространственной координаты на выражение ict, которое получено из предположений о 4-х мерной жидкости. Данный подход любопытен еще и тем, что в принципе позволяет изучать поверхностные явления в n-мерном пространстве путем замены его на комплексное пространство с действительными осями, принадлежащими изучаемой поверхности.
6. Живые системы
В главе, посвященной вопросу времени, мы пришли к тому, что для любой открытой, в том числе информационной системы, можно применить квантово-механическое описание. Тогда запишем выражение (32) для рассматриваемого нами живого объекта
![]() (46)
(46)
Далее можно применять для нашего объекта те же рассуждения, что и для квантового. Как известно, из свойства эрмитовости оператора ![]() следует [6]
следует [6]
![]() (47)
(47)
Из (47) следует, что у объекта должны существовать стационарные состояния. Физический смысл оператора ![]() в данном случае можно описать как воздействие внешней по отношению к объекту среды на него. Следовательно, в стационарном состоянии, внешнее воздействие среды на объект не приводит к изменению его внутреннего состояния. В связи с данным замечанием, будем считать, что стационарные состояния соответствуют обученной или адаптированной системе, а нестационарные - соответственно необученной и будем считать переходные процессы из одного стационарного состояния в другое обучением или адаптацией системы.
в данном случае можно описать как воздействие внешней по отношению к объекту среды на него. Следовательно, в стационарном состоянии, внешнее воздействие среды на объект не приводит к изменению его внутреннего состояния. В связи с данным замечанием, будем считать, что стационарные состояния соответствуют обученной или адаптированной системе, а нестационарные - соответственно необученной и будем считать переходные процессы из одного стационарного состояния в другое обучением или адаптацией системы.
Так как функция ψ - есть функция состояния, то она является скаляром. В то же время в стационарных состояниях в системе должно оставаться неизменным не только полный интеграл от ψ, но и пространственное распределение скалярных величин, то есть должна сохраняться внутренняя структура объекта. Это требование, принимая во внимание (13), выразиться в следующем соотношении
![]() (48)
(48)
То есть полная производная ![]() должна быть равна нулю. Рассматривая явления в жидкости (48), можно выразить через скалярный потенциал, а полную производную в (48) записать [2] как
должна быть равна нулю. Рассматривая явления в жидкости (48), можно выразить через скалярный потенциал, а полную производную в (48) записать [2] как
![]() (49)
(49)
![]() (50)
(50)
Там же, в [2], говориться, что условие (49) - есть условие параллельного переноса, то есть из (48) в стационарных состояниях оператор ![]() является оператором полной производной состояния.
является оператором полной производной состояния.
Вообще говоря, в (46) физический смысл оператора ![]() заключается в том, что система переходит из одного состояния в другое под воздействием некоторых факторов. Эти факторы делятся на две группы - внутренние и внешние по отношению к системе, так что можно выделить две составляющие оператора
заключается в том, что система переходит из одного состояния в другое под воздействием некоторых факторов. Эти факторы делятся на две группы - внутренние и внешние по отношению к системе, так что можно выделить две составляющие оператора![]() , обозначим соответственно внутренний оператор
, обозначим соответственно внутренний оператор ![]() , а внешний -
, а внешний - ![]() тогда
тогда
![]()
![]() (51)
(51)
Естественно, (51) имеет смысл только в том случае, когда можно говорить о внутренних и внешних воздействиях.
Сравнивая (51) с (50), можно записать
![]() (52)
(52)
соответственно
![]() (53)
(53)
![]() (54)
(54)
Введем представление вектора тока ![]() , такой что,
, такой что,
![]() (55)
(55)
![]() (56)
(56)
Теперь можно попробовать развернуть (53) и (54). Тогда из (53) получим
![]() (57)
(57)
Далее из (54) соответственно
![]() (58)
(58)
Раскрывая (58) получим для оператора потенциала
![]() (59)
(59)
или используя (56)
![]() (60)
(60)
Окончательно можно теперь переписать (51) в виде
 (61)
(61)
Следуя обозначениям из [8, с.70] , ![]() , то (61) можно теперь записать в новых обозначениях
, то (61) можно теперь записать в новых обозначениях
![]() (62)
(62)
Для систем, удовлетворяющих (48) получим систему двух уравнений
![]() (63)
(63)
![]()
Или, применяя выражение (42)
![]() (64)
(64)
![]()
При этом необходимо дополнительно выделить скалярные и векторные уравнения в (64). Для этого, однако, придется выделить скалярное и векторное слагаемое в тензоре ![]() .
.
Для чего мы все это проделали? Это нужно, в первую очередь, для того, чтобы попытаться раскрыть связь в уже известных, но, на первый взгляд, несвязанных явлениях. Как уже было сказано, (48) описывает стационарные системы, то есть такие системы, у которых не происходит изменения внутреннего состояния, или, по-другому, такие, которые можно рассматривать как твердые тела. Что касается другого класса систем, для которых несправедливо выражение (48), то такие системы по определению являются нестационарными. Это такие системы, в которых происходят фазовые превращения, сопровождающиеся изменением внутренней энергии и, соответственно, внутреннего времени. Очевидно, такие системы должны быть открытыми для того чтобы происходил энергетический обмен с внешней средой, однако обратное утверждение, вообще говоря, неверно, то есть определенный класс открытых систем может быть описан выражением (48).
Чтобы замкнуть (63), осталось выяснить как связан тензор ![]() c ψ-функцией. Здесь мы уже сделаем еще одно предположение - предположение о том, что H и E выражают соответственно магнитные и электрические поля. Очевидно, если связывать E и H с электромагнитным полем, то
c ψ-функцией. Здесь мы уже сделаем еще одно предположение - предположение о том, что H и E выражают соответственно магнитные и электрические поля. Очевидно, если связывать E и H с электромагнитным полем, то ![]() должен каким-то образом включать в себя выражения электрического заряда и тока, при этом, он, по определению, является тензором кривизны. Кроме того, выражение (42), полученное ранее, будет соответствовать, в таком случае, тензору электромагнитного поля.
должен каким-то образом включать в себя выражения электрического заряда и тока, при этом, он, по определению, является тензором кривизны. Кроме того, выражение (42), полученное ранее, будет соответствовать, в таком случае, тензору электромагнитного поля.
Из (64) можно заметить, что в отсутствие искривления i,3 - пространства (64) вырождается и в таком пространстве должно отсутствовать электромагнитные поле.
![]()
![]() (65)
(65)
![]()
Обратно, при наличии электромагнитного поля, возникает искривление - пространства. Ниже мы еще вернемся к обсуждению этого вопроса, и также вопроса о связи электромагнитного поля и гравитационной массы.
Похожие работы
... в лабораторных экспериментах и астрономических наблюдениях. Эти составные элементы космомикрофизики имеют свою специфику, к обсуждению которой мы и переходим. 4. Космические лучи Развитие физики элементарных частиц тесно связало с изучением космического излучения — излучения, приходящего на Землю практически изотропно со всех направлений космического пространства. Измерения интенсивности ...
... и искомыми величинами. Последовательность действий, которые надо выполнить, чтобы от исходных данных перейти к искомым величинам, называют алгоритмом. 2. Историческое развитие моделей элементарных частиц 2.1 Три этапа в развитии физики элементарных частиц Этап первый. От электрона до позитрона: 1897-1932гг (Элементарные частицы - "атомы Демокрита" на более глубоком уровне) Когда греческий ...
... тяготения электрона , где r2 ~ 2.5 × 10-31 см дает значения для порядка 1.8 эв. Масса покоя vm и vt практически не отличается от , если не учитывать поправок, вносимых mвирт 4,5 (n = 4,5), а именно, , . 5. Космологическая постоянная (плотность вакуума) и соотношение космических энергий Обнаруженная в последних астрономических наблюдениях, величина плотности вакуума составляет , Где r пл – ...
... непосредственно зафиксировать гравитоны очень сложно. Классификация частиц на лептоны, адроны и переносчики взаимодействий исчерпывает мир известных нам субатомных частиц. Каждый вид частиц играет свою роль в формировании структуры материи и Вселенной. 3. Теории элементарных частиц 3.1. Квантовая электродинамика (КЭД) Квантовая механика позволяет описывать движение элементарных частиц, но не ...

0 комментариев