Навигация
В заключение автор хотел бы подчеркнуть еще три момента
9. В заключение автор хотел бы подчеркнуть еще три момента.
Первый момент. Приведенные выше утверждения и соображения еще не стали “ общим местом” , еще не сформировали новый стереотип мышления геофизиков, занимающихся вопросами теории и практики интерпретации геофизических данных. Необходима огромная работа в этом направлении.
Второй момент. Изложенные в работе идеи никогда не станут эффективным средством решения задач геофизики, если на их основе не будет создано (по единому плану!) соответствующие компьютерные технологии. Нужна специальная (высокого уровня, желательно – государственного) программа создания таких технологий.
Третий момент. Изложенные в работе идеи не смогут быть быстро внедрены в сознание широкого круга геофизиков-производственников, если они не будут (притом самым быстрейшим образом) внедрены в высшее геофизическое образование. Подобное же внедрение требует целого ряда мероприятий, и прежде всего – написания принципиально новых учебников.
Автор надеется, что высказанные им соображения, утверждения и предложения станут предметом обсуждения на страницах геофизических журналов.
Обстоятельная конкретизация, в собственно математическом плане, приведенных в работе положений и утверждений, будет дана в серии последующих работ автора.
Список литературы
1. Страхов В.Н. Геофизика и математика // Физика Земли. 1995. № 12. С.4-23.
2. Страхов В.Н. Критический анализ классической теории линейных некорректных задач // Геофизика. 1999. № 3. С.3-9.
3. Страхов В.Н. Три парадигмы в теории и практике интерпретации потенциальных полей (анализ прошлого и прогноз будущего) // Известия секции наук о Земле РАЕН. 1999. № 2. С.95-135.
4. Страхов В.Н. О построении аналитических аппроксимаций аномальных гравитационных и магнитных полей // Основные проблемы теории интерпретации гравитационных и магнитных аномалий. М.: ОИФЗ РАН, 1999. С.65-125.
5. Страхов В.Н. Общая теория нахождения устойчивых приближенных решений систем линейных алгебраических уравнений с приближенно заданными правыми частями и матрицами, возникающих при решении задач геофизики // Вопросы теории и практики геологической интерпретации гравитационных, магнитных и электрических полей. М.: ОИФЗ РАН, 1997.С.38-42.
6. Страхов В.Н. Математический аппарат, используемый при конструировании алгоритмов нахождения устойчивых приближенных решений систем линейных алгебраических уравнений, возникающих в задачах гравиметрии и магнитометрии // Вопросы теории и практики геологической интерпретации гравитационных, магнитных и электрических полей. М.: ОИФЗ РАН, 1997. С.43-75.
7. Страхов В.Н. Экстремальные задачи, непараметрическая регуляризация и фильтрация в теории нахождения устойчивых приближенных решений систем линейных алгебраических уравнений с приближенно заданными правыми частями и матрицами // Вопросы теории и практики геологической интерпретации гравитационных, магнитных и электрических полей. М.: ОИФЗ РАН, 1997. С.76-88.
8. Страхов В.Н. Обобщенные QR-алгоритмы нахождения устойчивых приближенных решений систем линейных алгебраических уравнений с приближенно заданной правой частью, возникающих при решении линейных задач гравиметрии и магнитометрии // Вопросы теории и практики геологической интерпретации гравитационных, магнитных и электрических полей. М.: ОИФЗ РАН, 1997. С.87-88.
9. Страхов В.Н. Третья парадигма в теории и практике интерпретации потенциальных полей (гравитационных и магнитных аномалий). Ч. III // Электр. науч.-инф. журн. “Вестник ОГГГГН РАН”, № 1(3)'1998, М.:ОИФЗ РАН, 1998.
URL: http://www.scgis.ru/russian/cp1251/dgggms/1-98/3par3_00.htm
10. Страхов В.Н., Страхов А.В. Основные методы нахождения устойчивых приближенных решений систем линейных алгебраических уравнений, возникающих при решении задач гравиметрии и магнитометрии. I. М.: ОИФЗ РАН, 1999. 40 с.
11. Страхов В.Н., Страхов А.В. Основные методы нахождения устойчивых приближенных решений систем линейных алгебраических уравнений, возникающих при решении задач гравиметрии и магнитометрии. II. М.: ОИФЗ РАН, 1999. 52 с.
12. Страхов В.Н., Страхов А.В. К теории регуляризации линейных некорректных задач гравиметрии и магнитометрии. Ч. I // Электр. науч.-инф. журн. “Вестник ОГГГГН РАН”, № 1(7)'1999, М.:ОИФЗ РАН, 1999.
URL: http://www.scgis.ru/russian/cp1251/h_dgggms/1-99/strakh-1.htm#begin
13. Страхов В.Н., Страхов А.В. К теории регуляризации линейных некорректных задач гравиметрии и магнитометрии. Ч. II // Электр. науч.-инф. журн. “Вестник ОГГГГН РАН”, №3(9)'1999, М.:ОИФЗ РАН, 1999.
URL: http://www.scgis.ru/russian/cp1251/h_dgggms/3-99/strakh-2.htm#begin
14. Страхов В.Н., Страхов А.В. О решении систем линейных алгебраических уравнений с приближенно заданной правой частью, возникающих при решении задач гравиметрии и магнитометрии. М.: ОИФЗ РАН, 1999. 68 с.
15. Страхов В.Н., Страхов А.В. О решении систем линейных алгебраических уравнений, возникающих при решении задач гравиметрии и магнитометрии. 1. Редукция к системам в канонической форме // Докл. РАН. 1999. Т.368, № 4. С.545-548.
16. Страхов В.Н., Страхов А.В. О решении систем линейных алгебраических уравнений, возникающих при решении задач гравиметрии и магнитометрии. 2. Методы решения систем в канонической форме // Докл. РАН. 1999. Т.368, № 5. С.683-686.
17. Страхов В.Н., Страхов А.В.Аппроксимационный подход к решению задач гравиметрии и магнитометрии. I. Основная вычислительная проблема – регуляризация систем линейных алгебраических уравнений // Российский журнал наук о Земле. Т.1, № 4, июль 1999. С.271-299.
18. Страхов В.Н., Страхов А.В. Аппроксимационный подход к решению задач гравиметрии и магнитометрии. II. Новые методы нахождения устойчивых приближенных решений систем линейных алгебраических уравнений с приближенно заданной правой частью // Российский журнал наук о Земле. Т.1, № 5, сентябрь 1999. С.353-400.
19. Страхов В.Н. Основы новой теории регуляризации систем линейных аналитических уравнений с приближенными данными // Вопросы теории и практики геологической интерпретации гравитационных, магнитных и электрических полей: материалы 27-й сессии Международного семинара им. Д.Г. Успенского, Москва, 31 января – 4 февраля 2000 г. М.: ОИФЗ РАН, 2000. С.178-179.
20. Страхов В.Н. Субоптимальные алгоритмы нахождения устойчивых приближенных решений систем линейных алгебраических уравнений, возникающих при решении задач гравиметрии и магнитометрии // Докл. РАН. 2000. Т.373, № 4.
21. Страхов В.Н., Страхов А.В. Метод блочного координатного спуска для нахождения устойчивых приближенных решений систем линейных алгебраических уравнений с приближенно заданной правой частью большой и сверхбольшой размерности, возникающих при решении задач гравиметрии и магнитометрии // Докл. РАН. 2000.
Похожие работы
... чиновником, а мате- матические трактаты публиковались рядом с текстами по чайной церемонии или искусству икебана. Может быть даже в большой степени, чем японская культура, японская наука является изначально старательной ученицей китайской. В 646 г. благодаря реформам Тайка (тайка (яп.)- великая перемена), осуществленным императором Котоку, Япония приняла государ- ственную модель ...
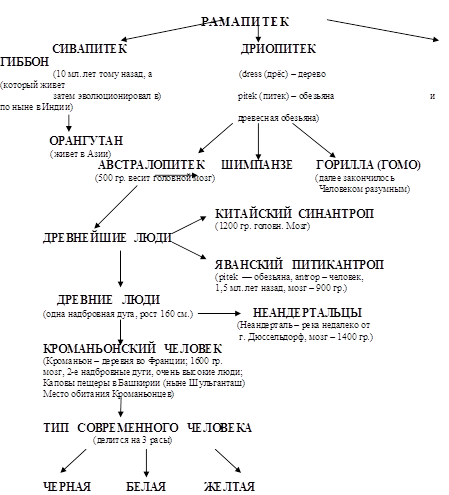
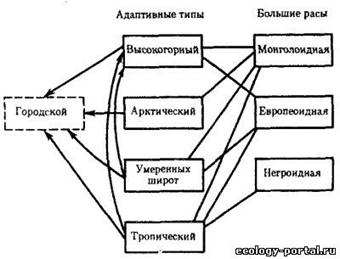
... важнейших вопросов антропологии, этнографии, демографии, исторической и медицинской географии. Расы - это территориальные группы людей, выделяемые на основе их генетического родства, которое проявляется в определенном физическом сходстве. Большинство отечественных антропологов различают три большие расы человечества - монголоидную ("желтую"), европеоидную ("белую") и негроидно-австролоидную (" ...


0 комментариев