Навигация
Математическое моделирование потребностей регионов в педагогических кадрах
Н.В. Перцев, Омский государственный педагогический университет, кафедра математического анализа
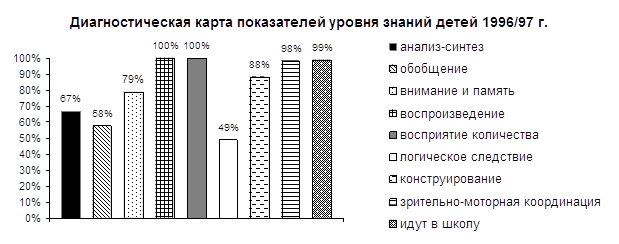
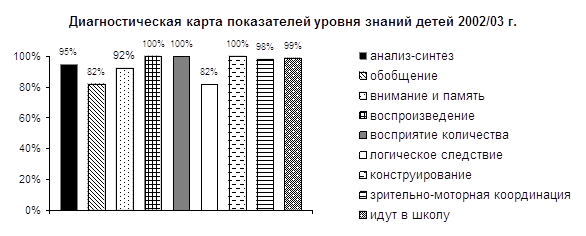
1. ВведениеПотребность некоторого региона в педагогических кадрах зависит от сочетания различных факторов демографического и социально-экономического характера. Эти факторы подвержены изменениям, которые влияют на количество учителей, работающих в школах региона, поэтому количество учителей может быть недостаточным, избыточным или соответствующим потребности в них. Соотношения между количеством работающих учителей и потребностью в них могут регулироваться за счет изменения некоторых параметров, численно выражающих влияние указанных факторов. К ним относятся, в частности, такие параметры, как средняя нагрузка учителей, граница допустимого возраста работы в школе (свыше пенсионного возраста), планы наборов в педвузы и училища, включая обучение на коммерческой основе. Конкретные значения этих параметров могут задаваться руководителями системы образования под влиянием реальной демографической и социально-экономической ситуации в регионе. В данной работе описан один из возможных подходов, позволяющий определять наиболее рациональные значения перечисленных параметров. Предлагаемый подход опирается на прогноз динамики количества учителей в школах региона с помощью математической модели. Определение искомых параметров сводится к постановке и решению задачи о нахождении оптимальных значений некоторых из параметров модели.
2. Описание моделиДинамика педагогических кадров в школах региона определяется балансовыми соотношениями между числом ежегодно увольняющихся и принимаемых на работу учителей. Пусть моменты времени t = t0, t1, t2, означают начало очередного учебного года, причем tk = tk-1+1, k=1, 2, , t0 - фиксировано, например, t0 = 1996. Примем, что величина y(t) задает общую численность учителей некоторой специальности, например, учителей математики в рассматриваемом регионе. Распределение численности учителей по возрасту будем описывать величинами y0(t), y1(t), , ym(t), такими, что y(t) = mi=0 yi(t). Здесь индекс i = 0, 1, , m означает условный возраст учителей, i=0 задает наименьший возраст (для выпускников педвузов и училищ), i = 1 - следующий возраст, , i = m задает границу допустимого возраста работы в школе (этой границей может быть пенсионный или больший возраст). Пусть qi(t) - средние доли ежегодно увольняющихся учителей условного возраста i, 0 qi(t) 1, 0 i m, (без учета выхода на пенсию). Тогда величина
|
равна общему количеству учителей, оставшихся работать в школах к началу очередного учебного года t (здесь и далее выражение [a] обозначает целую часть числа a).
Прием на работу в школы учителей условного возраста i будем описывать с помощью неотрицательных функций fi(t), которые показывают, сколько учителей данного условного возраста принято на работу в начале учебного года t, 0 i m. Предположим, что возрастной состав учителей y0(t-1), y1(t-1), , ym(t-1) в учебный год t-1 известен. Тогда возрастной состав учителей в учебный год t будет вычисляться по формулам
y0(t) = f0(t), y1(t) = [(1 - q0(t-1)) y0(t-1)] + f1(t), ..............................................................., yk(t) = [(1 - qk-1(t-1)) yk-1(t-1)] + fk(t), ................................................................, ym(t) = [(1 - qm-1(t-1)) ym-1(t-1)] + fm(t).
Установим вид функций fi(t), входящих в эти формулы. Пусть S(t) означает потребность региона в учителях фиксированной специальности на начало учебного года t. Значение S(t) определяется учебным планом по данному предмету и количеством классов-комплектов в школах региона при условии, что все учителя работают на ставку. Далее будем считать, что S(t) 1 при всех t t0. Примем, что (t) описывает среднюю нагрузку учителей на начало учебного года t. Предполагаем, что (t) может принимать некоторые значения из диапазона 1 (t) 2, где параметры 1 0, 2 1 задают нижнюю и верхнюю допустимые границы средней нагрузки учителей, например, 1 - 1,5 ставки. Зафиксируем S(t)/(t). Тогда величина d(t) = S(t)/(t)-y0(t) описывает разность между потребностью в учителях и их фактическим количеством на начало учебного года t. При d(t) 0 оставшихся учителей хватает, и новых учителей на работу можно не принимать. Если же d(t) 0, то можно либо увеличить (t), либо принять новых учителей, которые заполнят вакантные места. Общее количество вакантных мест V(t) и среднюю нагрузку (t) в учебном году t будем задавать соотношениями: если S(t) 1 y0(t), то V(t) = 0, (t) = 1, если же верно неравенство S(t) q1y0(t), то полагаем, что
V(t) = min{x}, x = 0, 1, 2, , 1(y0(t) + x) S(t) 2(y0(t) + x), (t) = S(t)/(y0(t) + V(t)).
Обозначим через A0(t), A1(t), , Am(t) количество учителей соответствующего условного возраста, обращающихся для трудоустройства в школы региона, по состоянию на начало учебного года t. Общее число A(t) учителей, принятых на работу к началу учебного года t, очевидно, равно
|
Весь набор условных возрастов 0 i m предcтавим в виде списка (i0, ,ik, , im), который устанавливает приоритетность приема на работу учителей определенного возраста. Например, если i0 = 0, то в первую очередь на работу принимаются молодые специалисты (выпускники педвузов и училищ). Далее полагаем
fi0(t) = min{Ai0(t), max{0, A(t)}}, fi1(t) = min{Ai1(t), max{0, A(t) - fi0(t)}},
|
Похожие работы
... ; технологическая функция имеет подфункции экономии учебного времени и учебного материала, устранения его дублирования и т.д. ГЛАВА 4. СОДЕРЖАНИЕ ИСНТРУМЕНТАЛЬНО-МЕТОДОЛОГИЧЕСКОГО ОБЕСПЕЧЕНИЯ ПЕДАГОГИЧЕСКОЙ ИНТЕГРАЦИИ 4.1. Типология интегративно-педагогического исследования В связи с поднимаемой в данном параграфе проблемой большой интерес вызывает монография В.М.Полонского "Оценки ...
... установить процентные соотношения различных показателей и на основании этого принять меры к усовершенствованию определенных сторон педагогической деятельности. Количественные или математические методы в педагогике являются аппаратом для прогнозирования, моделирования, компьютеризации педагогических процессов. 12. Содержание образования, как фундамент базовой культуры личности Для успешного ...
... нашего исследования математического развития ребенка дошкольного и младшего школьного возраста предложено возможное решение: непрерывная преемственная методическая система математического развития ребенка в системе дошкольного и начального школьного образования. Многолетняя апробация разработанной в ходе исследования системы хорошо себя зарекомендовала и подтвердила ее практическую значимость. ...
... ". Эта инициатива выдвинута 26 декабря 2003 года на совместном заседании Ассоциации "Роспрофтех", Академии профессионального образования и Российского клуба директоров. 2.2 Инновационные педагогические технологии на законодательном За время, прошедшее с принятия Федерального закона "Об утверждении Федеральной программы развития образования", в российской системе образования и ее финансовом ...
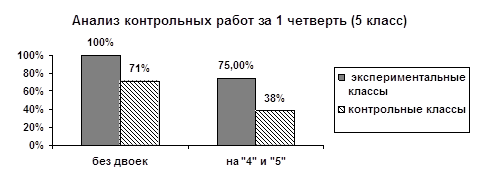
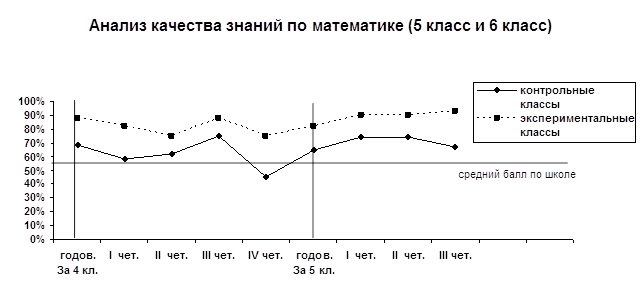
0 комментариев