Навигация
Некоторые подготовительные результаты
18285
знаков
0
таблиц
1
изображение
4. Некоторые подготовительные результаты.
Во введении мы уже говорили, что для задачи с ожиданием основной характеристикой качества обслуживания является длительность ожидания требованием начала обслуживания. Длительность ожидания представляет собой случайную величину, которую обозначим буквой g. Рассмотрим сейчас только задачу определения распределения вероятностей длительности ожидания в уже установившемся процессе обслуживания. Обозначим далее через P{g > t} вероятность того, что длительность ожидания превзойдет t, и через Pk{g > t} вероятность неравенства, указанного в скобке, при условии, что в момент поступления требования, в очереди уже находится k требований. В силу формулы полной вероятности имеем равенство
P{g > t}=
. (16)
Прежде чем преобразовать эту формулу к виду, удобному для пользования, приготовим некоторые необходимые нам для дальнейшего сведения. Прежде всего для случаев m=1 и m=2 найдем простые формулы для P0. несложные преобразования приводят к таким равенствам: при m=1
P0=1-r, (17)
а при m=2
(18)
Вычислим теперь вероятность того, что все приборы будут заняты в какой-то наудачу взятый момент. Очевидно, что эта вероятность равна
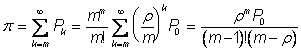(19)
Эта формула для m=1 принимает особенно простой вид:
p=r, (20)
при m=2
(21)
Напомним, что в формуле (19) r может принимать любое значение от 0 до m (включительно). Так что в формуле (20) r < 1, а в (21) r < 2.
5. определение функции распределения длительности ожидания.
Если в момент поступления требования в очереди уже находились k-m требований, то поскольку обслуживание происходит в порядке очередности, вновь поступившее требование должно ожидать, когда будут обслужены k-m+1 требований. Пусть qs(t) означает вероятность того, что за промежуток времени длительности t после поступления интересующего нас требования закончилось обслуживание ровно требований. Ясно, что k ³ m имеет место равенство
Так как распределение длительности обслуживания предположено показательным и независящим ни от того, сколько требований находится в очереди, ни от того, как велики длительности обслуживания других требований, то вероятность за время t не завершить ни одного обслуживания (т.е. вероятность того, что не освободится ни один из приборов) равна
Если все приборы заняты обслуживанием и еще имеется достаточная очередь требований, которые ожидают обслуживания, то поток обслуженных требований будет простейшим. Действительно, в этом случае все три условия - стационарность, отсутствие последействия и ординарность - выполнены. Вероятность освобождения за промежуток времени t ровно s приборов равна (это можно показать и простым подсчетом)
Итак,
и, следовательно,
Но вероятности Pk известны:
поэтому
очевидными преобразованиями приводим правую часть последнего равенства к виду
Из формул (13) и (19) следует, что 
, поэтому при t>0
(22)
Само собой разумеется, что при t<0 
.
Функция 
имеет в точке t=0 разрыв непрерывности, равный вероятности застать все приборы занятыми.
Похожие работы
... и эффективным средством выработки оптимальных управленческий решений, главной особенностью которых в современных условиях становится их своевременность. 2 Применение теории массового обслуживания в экономическом анализе 2.1 Теория массового обслуживания Теория массового обслуживания – вероятностные модели реальных систем обслуживания населения, при которых время обслуживания будет ...
... сообщение (требование). В таком случае, если в очереди есть сообщения * (требования), переходим в очереди новое состояние: уменьшаем количество сообщений * (требований), ожидающих в обслуживания очереди на 1. */ if (this.getCurrentPort().getName().equals("fromNext")) { serverIsFree = true; /* Если в очереди было одно сообщение (требование), то теперь там не будет ни ...
... коммерческой деятельности. Для решения перечисленных задач существует эффективный метод моделирования, включающий и объединяющий достижения разных наук, в том числе математики. 1.2 Моделирование систем массового обслуживания Переходы СМО из одного состояния в другое происходят под воздействием вполне определенных событий - поступления заявок и их обслуживания. Последовательность появления ...
... сколько их уже исправно и ждет наладки. Классификация СМО далеко не ограничивается приведенными разновидностями, но этого достаточно.2. Системы массового обслуживания с ожиданием 2.1 Одноканальная СМО с ожиданием Рассмотрим простейшую СМО с ожиданием — одноканальную систему (n - 1), в которую поступает поток заявок с интенсивностью ; интенсивность обслуживания (т.е. в среднем непрерывно ...
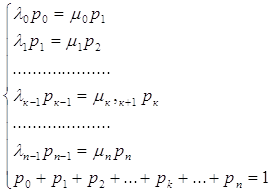
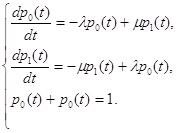
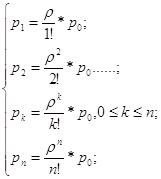
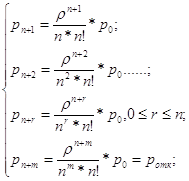
0 комментариев