Навигация
Описание тестовой диагностики
37815
знаков
9
таблиц
6
изображений
1.3. Описание тестовой диагностики.
Проблема тестового диагностирования цифровых схем возникает на различных этапах их производства и эксплуатации и включает взаимосвязанные задачи. Первая из них заключается в определении, в каком состоянии находится исследуемая схема.[3] Основным состоянием цифровых схем является исправное - это такое техническое состояние схемы, при котором она удовлетворяет всем требованиям, установленным технической документацией. В противном случае схема находится в одном из неисправных состояний.
Если установлено, что цифровая схема неисправна, то решается вторая задача: осуществляется поиск неисправности схемы, цель которого - определение места и вида неисправности.
Из множества различных видов неисправностей выделяется класс логических неисправностей, которые изменяют логические функции элементов цифровой схемы. Для их описания в большинстве случаев используются следующие математические модели.
Константные неисправности: константный нуль и константная единица, что означает наличие постоянного уровня логического нуля или логической единицы на входах и выходе неисправного логического элемента.
Неисправности типа “короткое замыкание” (мостиковые неисправности) появляются при коротком замыкании входов и выходов логических элементов и подразделяются на два вида: неисправности, вызванные коротким замыканием входов логического элемента, и неисправности типа обратной связи.
Инверсные неисправности описывают физические дефекты цифровых схем, приводящие к появлению фиктивного инвертора по входу или выходу логического элемента, входящего в данную схему.
Неисправности типа “перепутывание” заключаются в перепутывании связей цифровой схемы и вызываются ошибками, возникающими при проектировании и производстве цифровых схем, которые изменяют функции, выполняемые схемой.
Классическая стратегия тестирования цифровых схем основана на формировании тестовых последовательностей, позволяющих обнаруживать заданные множества их неисправностей. При этом, для проведения процедуры тестирования, хранятся как сами тестовые последовательности, так и эталонные выходные реакции схем на их воздействие. В процессе тестирования при соответствии полученных реакций схемы эталонным она считается исправной, в противном случае схема содержит неисправность и находится в неисправном состоянии.
Структурные блоки, на которые разбивается задача диагностики, приведены на рис. 1.1.
 | |||
 | |||
Рис.1.1. Основные функциональные блоки, используемые при тестировании цифровой схемы.
ГТВ – генератор тестовых воздействий (генератор М- последовательности)
ЦС – цифровая схема
МСА – многоканальный сигнатурный анализатор
Блок эталонных реакций - блок, хранящий сжатые выходные реакции
Логическая взаимосвязь функциональных блоков построена следующим образом: с генератора тестовых воздействий через цифровую схему сигналы поступают на схему сжатия информации (сигнатурный анализатор). Сжатые выходные реакции (сигнатуры) попадают на схему сравнения, где они сравниваются с эталонными сигнатурами, которые хранятся в блоке эталонных реакций. Далее информация попадает в устройство вывода информации о состоянии схемы.
Все данные блоки реализованы в виде математической модели на компьютере.
В данной работе в качестве блока сжатия информации смоделирован многоканальный сигнатурный анализатор.
1.4. Принципы генерирования случайных и псевдослучайных последовательностей.
В задачах активных экспериментальных исследований современных сложных технических систем с применением статистических методов важное место принадлежит генерированию сигналов возбуждения.[4] Диктуется это не только необходимостью подачи на объект требуемого числа воздействий с заданными свойствами, но и максимальной скорости их выработки. Одним из наиболее распространённых в настоящее время методов формирования таких процессов является преобразование сигналов, получаемых с помощью так называемых генераторов белого шума (ГБШ). В применении к цифровым методам генерирования под белым шумом понимается последовательность некоррелированных чисел или цифр, распределённых, как правило, по равномерному закону.
Известны два основных метода получения цифрового белого шума: физический - генерирование случайных двоичных чисел с помощью специальных устройств - генераторов случайных чисел (ГСЧ); математический - формирование псевдослучайных числовых последовательностей (ПСЧП) по специальным программам или с использованием генераторов псевдослучайных чисел (ГПСЧ).
Принцип действия ГСЧ состоит в преобразовании случайного сигнала на выходе физического источника шума в импульсную последовательность с вероятностью появления импульса p(1)=0,5.
Общими и наиболее существенными недостатками, затрудняющими применение ГСЧ, являются ограниченное быстродействие, определяемое первичным аналоговым источником шума; низкая стабильность основных вероятностных характеристик, объясняемая нестабильностью первичных источников, дрейфом параметров преобразующих схем, источников питания и др., что требует периодической статистической проверки качества генерируемой последовательности; сложность аппаратурной реализации, вызываемая наличием нескольких источников питания; невозможность воспроизведения и предсказания генерируемых последовательностей в силу их случайной природы и т.д.
Указанные недостатки физических ГСЧ явились причиной всё более широкого распространения математических методов получения шумовых числовых последовательностей. Мгновенные значения таких псевдослучайных последовательностей в отличие от случайных в принципе могут быть предсказаны заранее. В то же время все оценки статистических характеристик конкретной реализации ПСЧП совпадают с оценками соответствующей ей случайной выборки. Любую статистическую характеристику псевдослучайной числовой последовательности можно получить, используя реализацию длиной в один период повторения ПСЧП. Для истинно случайной последовательности это потребовало бы бесконечно большую длину реализации. Искусственное увеличение периода ПС - сигнала неограниченно приближает его структуру к структуре одной из возможных реализаций истинно случайного процесса. Однако и при ограниченных величинах периода в определённых условиях псевдослучайные числовые последовательности могут заменить случайные. При анализе псевдослучайной реализации равной или меньшей длине периода вообще практически невозможно определить, является ли она отрезком регулярной или случайной последовательности. С другой стороны, если записать конкретную случайную реализацию на каком-либо носителе, и периодически воспроизводить её, то получим регулярную ПСЧП.
Таким образом, с точки зрения реальных характеристик трудно установить границу между случайными и псевдослучайными числовыми последовательностями. В то же время применение ПСЧП имеет ряд существенных преимуществ: периодический характер псевдослучайного сигнала обуславливает низкий уровень дисперсии оценок, получаемых при усреднении в течение целого числа периодов; характеристики ПСЧП абсолютно стабильны и определяются алгоритмом формирования псевдослучайных чисел; последовательность можно повторить с любого желаемого участка реализации, для чего не требуется сложных запоминающих устройств и др.
Работу генератора М-последовательности, сумматоры по модулю два которого включены в межразрядные связи, а порождающий полином равен 
M(x)= 1
1x2x2...mxm, можно описать выражением
AM(k)=VMAM(k-1),
где m-мерные вектора AM(k)=(a1M(k), a2M(k),..., amM(k)) и AM(k-1)= =(a1M(k-1), a2M(k-1),..., amM(k-1)) определяют состояния РС генератора в k-й и (k-1)-й такты работы соответственно, а матрица VM, описывающая структуру генератора, имеет вид:
0 0 0 . . . 0 1
1 0 0 . . . 0 1
VM= 0 1 0 . . . 0 2
. . . . . . . .
0 0 0 . . . 1 m-1
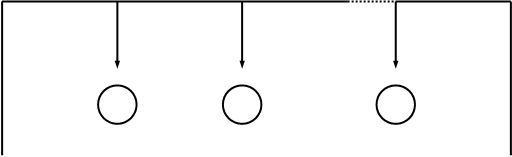
Структурная схема генератора М - последовательности, построенного по способу включения сумматоров в межразрядные связи регистра сдвига представлена на рис.1.2.
12m-1
 |  |  | |||||||||||||||||
 |  |  | |||||||||||||||||
 |  |  |  | ||||||||||||||||
a1(k)a2(k)a3(k)am(k)
Рис.1.2. Генератор М - последовательности с сумматорами по модулю два,
стоящими в межразрядных связях регистра сдвига:
Можно показать [5], что между состояниями AM(k) и A(k) РС генераторов обоих типов при AM(0)= A(0)=1000...0 существует зависимость, определяемая соотношением:
a1M(k) m m-1 m-2 . . . 2 1 a1(k)
a2M(k) 0 m m-1 . . . 3 2 a2(k)
a3M(k) = 0 0 m . . . 4 3 a3(k)
. . . . . . . . . . . . . . . . . . . . .
amM(k) 0 0 0 . . . 0 0 am(k)
При этом, порождающий полином (x) M-последовательности, генератор которой содержит сумматоры по модулю два в цепи обратной связи, является взаимно обратным к полиному M(x), т.е. (x)= M-1(x)=xmM(x-1).
Похожие работы
... Студент группы 220352 Чернышёв Д. А. Справка— отчет о патентном и научно- техническом исследовании Тема выпускной квалификационной работы: телевизионный приёмник с цифровой обработкой сигналов. Начало поиска 2. 02. 99. Окончание поиска 25.03.99 Предмет поиска Страна, Индекс (МКИ, НКИ) № ...
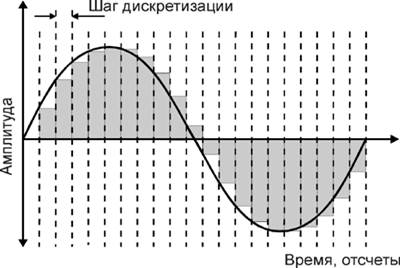
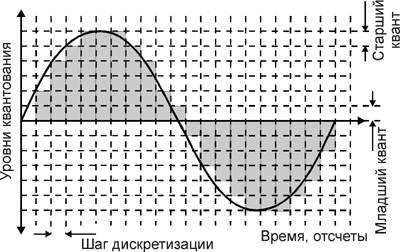
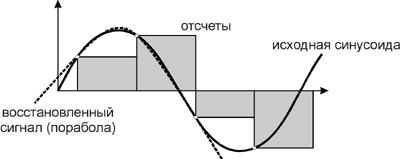
... 1 – «-» Причем 1-ый разряд слева – знаковый разряд. 16 14 12 10 8 6 4 2 Т 2Т 2. Связи между аналоговыми и дискретными сигналами. При обработке сигнала на ЭВМ необходимо в максимальной степени, чтобы дискретный или цифровой сигнал содержал все признаки аналогового сигнала. При дискретизации возможна потеря информации, которая ...
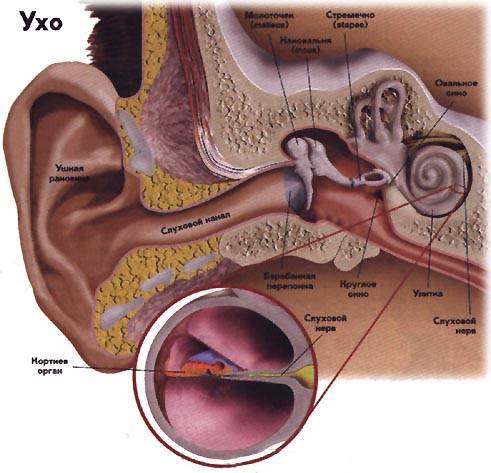
... примерно 6%. В общем, в районе 1 - 4 кГц чувствительность уха по всем параметрам максимальна, и составляет не так уж и много, если брать не логарифмированные значения, с которыми приходится работать цифровой технике. Примите на заметку - многое из того, что происходит в цифровой обработке звука, может выглядеть ужасно в цифрах, и при этом звучать неотличимо от оригинала. В цифровой обработке ...
... несущими и амплитудно-фазовая модуляция с одной боковой полосой (АФМ-ОБП). 3. Выбор длительности и количества элементарных сигналов, используемых для формирования выходного сигнала В реальных каналах связи для передачи сигналов по частотно ограниченному каналу используется сигнал вида , но он бесконечен во времени, поэтому его сглаживают по косинусоидальному закону. , где - ...
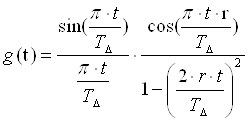
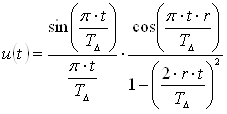
0 комментариев