Навигация
Алгоритм построения многоканального сигнатурного анализатора
37815
знаков
9
таблиц
6
изображений
2.5. Алгоритм построения многоканального сигнатурного анализатора.
Для заданных значений 
и 
, где определяет достоверность диагностирования, алгоритм построения многоканального сигнатурного анализатора состоит из следующих этапов.
1. Вычисляются постоянные коэффициенты 
где 
2. Определяются коэффициенты 
причём значения коэффициентов 
вычисляются на основании соответствующей системы уравнений, а значения остальных коэффициентов определяются согласно выражению 
3. Строится функциональная схема многоканального сигнатурного анализатора на основании полученной системы уравнений
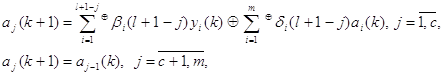
При этом используются результаты этапов 1 и 2, позволяющих однозначно определить топологию связей многовходовых сумматоров по модулю два, на выходах которых формируются значения 
.
2.6. Применение многоканальных анализаторов для диагностики неисправностей.
С помощью многоканальных сигнатурных анализаторов можно существенно ускорить процедуру контроля цифровых схем, которая практически увеличивается в n раз, где n – количество входов применяемого анализатора. В случае совпадения реально полученной сигнатуры с её эталонным значением считается, что с достаточно высокой вероятностью проверяемая цифровая схема находится в исправном состоянии. На этом процедура её исследования оканчивается. В противном случае, когда схема содержит неисправности, реальная сигнатура, как правило, отличается от эталонной, что служит основным аргументом для принятия гипотезы о неисправном состоянии схемы. В тоже время вид полученной сигнатуры не несёт никакой дополнительной информации о характере возникшей неисправности. Более того, остаётся открытым вопрос о том, какие из n анализируемых последовательностей, инициирующих реальную сигнатуру, содержат ошибки, т.е. возникает задача локализации неисправности с точностью до последовательности, несущей информацию о её присутствии. Рассмотрим возможные варианты решения данной задачи для случая применения n – канальных анализаторов.
Предварительно докажем следующую теорему.
Теорема. Суммарная сигнатура S(x), полученная для последовательностей 
на n – канальном сигнатурном анализаторе, равна поразрядной сумме по модулю два сигнатур 
, 
, причём каждая из сигнатур 
, формируется для последовательности 
при условии, что 
.
Доказательство. В n – канальном анализаторе n входных последовательностей преобразуются в одну вида:
Такая входная последовательность, анализируемая n канальным сигнатурным анализатором, описывается следующим двоичным полиномом:
, (2.6.1)
который состоит из суммы по модулю два полиномов вида:
, (2.6.2)
описывающих выходные последовательности 
. Каждый полином 
можно представить в виде соотношения:
, (2.6.3)
где 
-полином, взаимно обратный полиному 
, используемому для реализации n – канального сигнатурного анализатора; 
- сигнатура последовательности 
.
Просуммировав по модулю два правые и левые части равенства (2.6.3), получим, что полином 
будет определяться как
(2.6.4)
для которого также справедливо соотношение 
, т.е.
(2.6.5)
В результате сравнения двух последних равенств можно заключить, что суммарная сигнатура S(x), полученная для последовательностей 
равна поразрядной сумме по модулю два сигнатур каждой из входных последовательностей:
(2.6.6)
что и требовалось доказать.
Основной результат данной теоремы, выраженный соотношением (2.6.5), справедлив для примитивного полинома и произвольных значений n и l. Следствием этой теоремы является возможность определения эталонной сигнатуры для произвольного множества входных последовательностей. Так, эталонное значение сигнатуры для первой, второй и пятой последовательностей будет вычисляться как
Используя результаты теоремы, можно формализовать процедуру контроля цифровой схемы. При этом входными последовательностями 
этого анализатора в общем случае могут быть последовательности, формируемые на входных, промежуточных и выходных полюсах схемы, для которых в результате предварительных исследований определены значения эталонных сигнатур 
. Не нарушая общности, предположим, что n=2d, и представим процедуру контроля в виде следующего алгоритма.
Алгоритм контроля цифровой схемы локализацией неисправности до первой последовательности, содержащей вызванные ею ошибки.
В результате анализа n=2d реальных последовательностей 
на n – канальном анализаторе определяется значение сигнатуры S*(x), которое соответствует соотношению:
По выражению
вычисляется эталонное значение сигнатуры S(x).
Реальное значение сигнатуры S*(x) сравнивается с эталонной сигнатурой S(x). В случае выполнения равенства S*(x) и S(x) считается процедура диагностики оконченной. В противном случае, когда S*(x)¹S(x) выполняется следующий этап алгоритма.
Все множество входных последовательностей разбивается на две группы, причём номера последовательностей 
составляют множество А1={1,2,3…n/2}, а номера последовательностей 
составляют множество А2={n/2+1,n/2+2,…n}. Значению i присваивается значение 1.
В результате анализа реальных последовательностей, номера которых задаются множеством А1 на n – канальном сигнатурном анализаторе при условии, что последовательности, номера которых определяет множество А2, являются нулевыми, определяется значение реальной сигнатуры.
На основании выражения
определяем S(x).
Проверяется справедливость равенства S*(x)=S(x), в случае выполнения множество А1 заменяется элементами множества А2.
Значение переменной i увеличивается на 1 и сравнивается с величиной n, если i<n, то совершают вышеприведённые действия с элементами множества А2.
Единственный элемент множества А1 представляет собой номер ошибочной последовательности.
Процедура контроля цифровой схемы считается законченной.
2.7. Оценка достоверности многоканального сигнатурного анализатора.
Учитывая эквивалентность функционирования n - канального сигнатурного анализатора и соответствующего ему одноканального анализатора относительно результата сжатия n входных последовательностей 
логично оценить достоверность МСА, используя результаты, полученные для одноканального сигнатурного анализатора. Действительно, в случае применения примитивного полинома вероятность необнаружения ошибок в последовательностях многоканальным сигнатурным анализатором для 
где m – старшая степень порождающего полинома, будет определяться соотношением:
Это соотношение справедливо для любого соотношения 
и , произведение которых равно 2m-1.[6] Приведённая интегральная характеристика эффективности МСА, также как и характеристика одноканального сигнатурного анализатора, является достаточно приближённой оценкой, справедливой для общих допущений. Более полной характеристикой МСА будет распределение вероятностей 
необнаружения возникшей ошибки кратности m в анализируемых последовательностях . При этом численное значение указанных вероятностей, как и в случае одноканального анализатора, определяется выражениями:
Попытка применить это выражение для оценки значений при анализе последовательности 
, когда 
на n – канальном анализаторе не всегда позволяет получить верные результаты.
Теорема. Множество ошибок последовательности 
необнаруживаемых одноканальным СА, реализованном на основании примитивного полинома , старшая степень которого равна m, соответствует множеству необнаруживаемых ошибок n = 2d – канальным анализатором, (d – целое положительное число) при условии отсутствия ошибок в последовательностях 
.
Таким образом, достоверность многоканального сигнатурного анализатора может быть оценена либо интегральной величиной 
, либо распределением вероятностей необнаружения m - кратной ошибки в анализируемых последовательностях . Более предпочтительным значением n является значение, удовлетворяющее требованию n = 2d. Анализ последовательности 
для 
на подобном анализаторе будет эквивалентен анализу на соответствующем одноканальном анализаторе.
Похожие работы
... Студент группы 220352 Чернышёв Д. А. Справка— отчет о патентном и научно- техническом исследовании Тема выпускной квалификационной работы: телевизионный приёмник с цифровой обработкой сигналов. Начало поиска 2. 02. 99. Окончание поиска 25.03.99 Предмет поиска Страна, Индекс (МКИ, НКИ) № ...
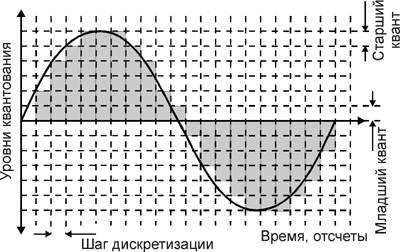
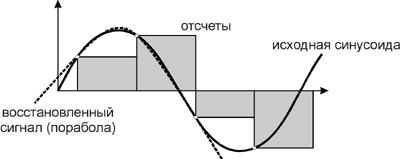
... 1 – «-» Причем 1-ый разряд слева – знаковый разряд. 16 14 12 10 8 6 4 2 Т 2Т 2. Связи между аналоговыми и дискретными сигналами. При обработке сигнала на ЭВМ необходимо в максимальной степени, чтобы дискретный или цифровой сигнал содержал все признаки аналогового сигнала. При дискретизации возможна потеря информации, которая ...
... примерно 6%. В общем, в районе 1 - 4 кГц чувствительность уха по всем параметрам максимальна, и составляет не так уж и много, если брать не логарифмированные значения, с которыми приходится работать цифровой технике. Примите на заметку - многое из того, что происходит в цифровой обработке звука, может выглядеть ужасно в цифрах, и при этом звучать неотличимо от оригинала. В цифровой обработке ...
... несущими и амплитудно-фазовая модуляция с одной боковой полосой (АФМ-ОБП). 3. Выбор длительности и количества элементарных сигналов, используемых для формирования выходного сигнала В реальных каналах связи для передачи сигналов по частотно ограниченному каналу используется сигнал вида , но он бесконечен во времени, поэтому его сглаживают по косинусоидальному закону. , где - ...
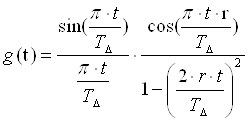
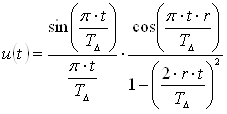
0 комментариев