Навигация
Особенности построения генераторов тестовых последовательностей
37815
знаков
9
таблиц
6
изображений
1.5. Особенности построения генераторов тестовых последовательностей.
При компактном тестировании для реализации тестовой последовательности используются простейшие методы, позволяющие избежать сложной процедуры синтеза.[2] К ним относятся следующие процедуры синтеза:
Формирование всевозможных входных тестовых наборов, т.е. полного перебора двоичных комбинаций. В результате применения подобного алгоритма генерируются так называемые счётчиковые последовательности.
Формирование случайных тестовых наборов с требуемыми вероятностями появления единичного и нулевого символов по каждому входу ЦС.
Формирование псевдослучайных тестовых последовательностей.
Основным свойством этих алгоритмов является то, что в результате их применения воспроизводятся последовательности очень большой длины. Поэтому на выходах проверяемой ЦС формируются её реакции, имеющие ту же длину. При этом если для генераторов тестовых последовательностей, формирующих счётчиковые, случайные и псевдослучайные последовательности, не существует проблемы их запоминания и хранения, то для выходных реакций каждой схемы такая проблема имеет место быть. Простейшим решением, позволяющим сократить объём хранимой информации об эталонных выходных реакциях, являются методы компактного тестирования.
Глава 2.Сигнатурный анализ.
2.1. Описание сигнатурного анализа.
В настоящее время в новой технике тестирования цифровых схем сигнатурный анализ применяется наиболее часто. Это было предопределено несколькими причинами [5], например такими: Равномерность закона распределения вероятности 
необнаружения ошибки кратности i и Множество необнаруживаемых ошибок V
кратности i включает в себя маловероятные конфигурации ошибочных бит в последовательности данных.
Построить сигнатурный анализатор можно двумя способами: 1)метод деления полиномов и 2)метод свёртки.
Главная идея сигнатурного анализа при использовании метода деления полинома на полином основывается на выполнении операции деления многочленов. В качестве делимого используется поток данных, формируемых на выходе анализируемого цифрового узла, который может быть представлен как многочлен p(x) степени 
-1, где - длина потока. Делителем служит примитивный неприводимый полином 
(x), в результате деления на который получается частное q(x) и остаток S(x), связанные соотношением
p(x)= q(x) 
(x)+ S(x),
где остаток S(x), представляющий собой полином степени, меньшей чем m=deg(x), называется сигнатурой.
M2 D TT M2 D TT M2 D TT
P(x)
C 0 C 1 C m-1
ТИ
 | |||||
 | |||||
 | |||||
& & &
 | |||
 | |||
0=1 1 m-1
Рис.2.1. Функциональная схема сигнатурного анализатора, построенного
по методу деления полиномов.
 | |
M2 M2
 |  | ||||
 |
P(x) & & &
M2 D TT D TT D TT
C 0 1 C 1 m-1 C m-1 m=1
ТИ
Рис.2.2. Функциональная схема сигнатурного анализатора, построенного
по методу свёртки.
При использовании метода свёртки сигнатурного анализа как метода сжатия реакций цифровой схемы сигнатура R6=a1()a2()...am() формируется по алгоритму:
a1(0)=a2(0)=...=am(0)=0, (2.1.1)
a1(k)=y(k)
i ai(k-1), (2.1.2)
aj(k)=aj(k-1), j=2,3...m, k=1,2... , (2.1.3)
где i
{0,1}, i=1,2...m, определяются на основании порождающего полинома (x)=11x12x2...mxm, используемого для реализации сигнатурного анализатора.
Однако, результат свёртки c(x) последовательности на сигнатурном анализаторе не есть остаток s(x) от деления на полином (x). В то же время между c(x) и s(x) существует однозначная связь, определяемая соотношением
1 2 ...m-1 1
2 3 ... 1 0
s(x)= c(x)
........................................
m-1 1 ... 0 0
1 0 ... 0 0
2.2. Одноканальный сигнатурный анализатор.
Типовая структурная схема сигнатурного анализатора состоит из регистра сдвига и сумматора по модулю 2, на входы которого подключены выходы разрядов регистра в соответствии с порождающим полиномом(x) (рис. 2.3.) [5]. Управляющими сигналами сигнатурного анализатора являются СТАРТ, СТОП и СДВИГ. Сигналы СТАРТ и СТОП формируют временной интервал, в течение которого осуществляется процедура сжатия информации на анализаторе. Под действием сигнала СТАРТ элементы памяти регистра сдвига устанавливаются в исходное состояние, как правило, нулевое, а сам регистр начинает выполнять функцию сдвига на один разряд вправо под действием синхронизирующих сигналов СДВИГ. По приходу каждого синхронизирующего импульса в первый разряд регистра сдвига записывается информация, соответствующая выражению (2.1.2), где y(k)
{0,1} - k-й символ сжимаемой последовательности {y(k)}, k=1,2... ; i{0,1} - коэффициенты порождающего полинома (x); ai(k-1){0,1} - содержимое i-го элемента памяти регистра сдвига в k-1 такт. Процедура сдвига информации в регистре описывается соотношением (2.1.3). Причём , как правило, принимается равным или
Сигнатура
M2 RG
 | |||||||||
 | |||||||||
 |  |  | |||||||
Сдвиг Старт Стоп
Рис.2.3. Структурная схема сигнатурного анализатора.
меньше величины 2m-1 и соответственно определяет длину сжимаемой последовательности. По истечении тактов функционирования сигнатурного анализатора на его элементах памяти фиксируется двоичный код, который представляет собой сигнатуру, отображаемую в виде 16-ричного кода.
Таким образом, путём формирования тестовой последовательности на входах анализируемого цифрового устройства для каждого его полюса находим эталонные значения сигнатур, множество которых запоминается и в дальнейшем используется для сравнения со значениями сигнатур, снимаемых с проверяемых устройств. Любое отличие реально полученной сигнатуры от эталонной свидетельствует о том, что полюс схемы функционирует отлично от случая исправного состояния устройства. Причина, вызвавшая отличие сигнатур на данном полюсе, может быть установлена последовательным анализом сигнатур от указанного полюса к входам устройства.
Эффективность использования такого сигнатурного анализатора ограничивается наличием в нём только одного информационного входа, в то время как количество выходов сложных цифровых узлов достигает значительных величин. Исследование подобных узлов осуществляется с использованием нескольких сигнатурных анализаторов, путём свёртки по модулю два выходных последовательностей или с применением некоторых других схемных решений.[1] Применение таких подходов для анализа многовыходных цифровых схем приводит или к существенному увеличению аппаратурных затрат, или к уменьшению величины вероятности P обнаружения ошибки. Поэтому для многовыходных цифровых узлов создание высокоэффективных цифровых анализаторов весьма актуально.
Похожие работы
... Студент группы 220352 Чернышёв Д. А. Справка— отчет о патентном и научно- техническом исследовании Тема выпускной квалификационной работы: телевизионный приёмник с цифровой обработкой сигналов. Начало поиска 2. 02. 99. Окончание поиска 25.03.99 Предмет поиска Страна, Индекс (МКИ, НКИ) № ...
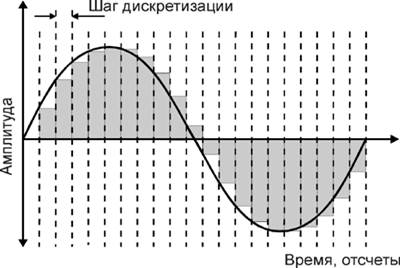
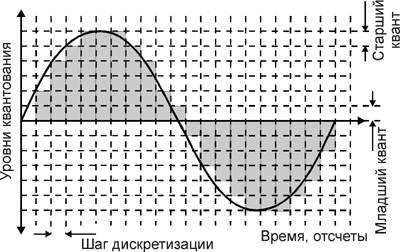
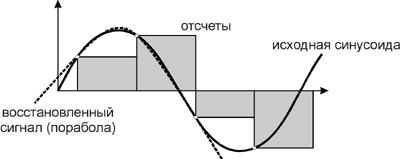
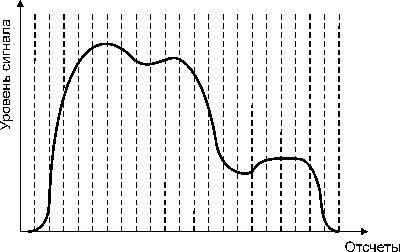
... 1 – «-» Причем 1-ый разряд слева – знаковый разряд. 16 14 12 10 8 6 4 2 Т 2Т 2. Связи между аналоговыми и дискретными сигналами. При обработке сигнала на ЭВМ необходимо в максимальной степени, чтобы дискретный или цифровой сигнал содержал все признаки аналогового сигнала. При дискретизации возможна потеря информации, которая ...
... примерно 6%. В общем, в районе 1 - 4 кГц чувствительность уха по всем параметрам максимальна, и составляет не так уж и много, если брать не логарифмированные значения, с которыми приходится работать цифровой технике. Примите на заметку - многое из того, что происходит в цифровой обработке звука, может выглядеть ужасно в цифрах, и при этом звучать неотличимо от оригинала. В цифровой обработке ...
... несущими и амплитудно-фазовая модуляция с одной боковой полосой (АФМ-ОБП). 3. Выбор длительности и количества элементарных сигналов, используемых для формирования выходного сигнала В реальных каналах связи для передачи сигналов по частотно ограниченному каналу используется сигнал вида , но он бесконечен во времени, поэтому его сглаживают по косинусоидальному закону. , где - ...
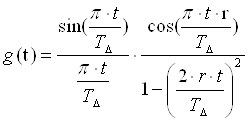
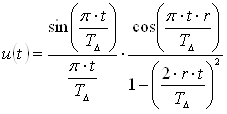
0 комментариев