Навигация
3.1.4. Выводы и рекомендации.
Результаты экспериментальных исследований, приведенных выше, дают основание рекомендовать две конструкции фрезы: первая конструкция фрезы отличается от стандартной лишь геометрическими параметрами режущих лезвий, поэтому практически не требует дополнительных затрат на ее изготовление.
Геометрические параметры этой фрезы имеют значения, приведенные в таблице (табл. 3.1.2).
Таблица 3.1.2
Геометрические параметры фрезы.
| | 1 | | | |
| 70 | 15 | 0 | 16 | 0 |
Вторая конструкция фрезы имеет такую же геометрию, как и первая, но отличается от нее наличием одного или нескольких зачистных зубьев (см. рис. 3.2), имеющих вспомогательную режущую кромку длиной 1.5 2 мм с 1 = 0. Остальная часть режущих кромок этих зубьев имеет 1 = 15. Фрезерование целесообразно проводить со скоростью резания = 80 м/мин и подачей Sz = 0.08 мм/зуб.
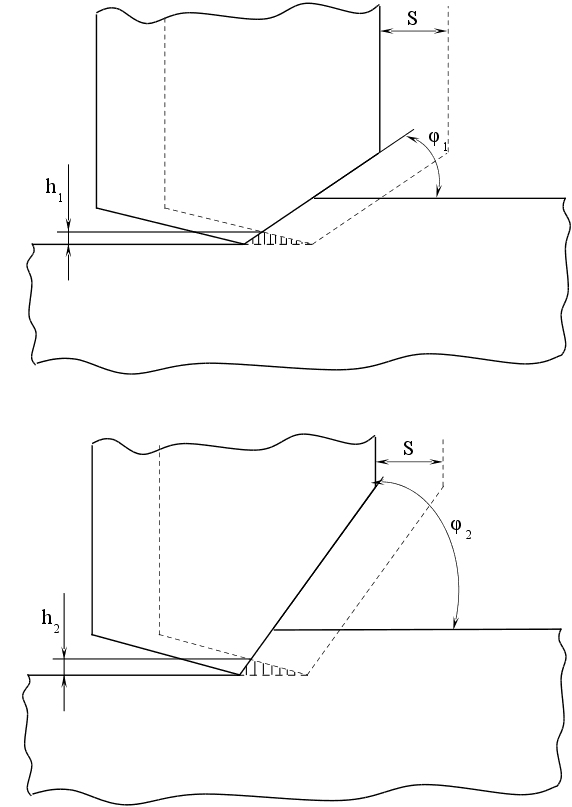
рис. 3.2 Влияние угла в плане на высоту заусенцев
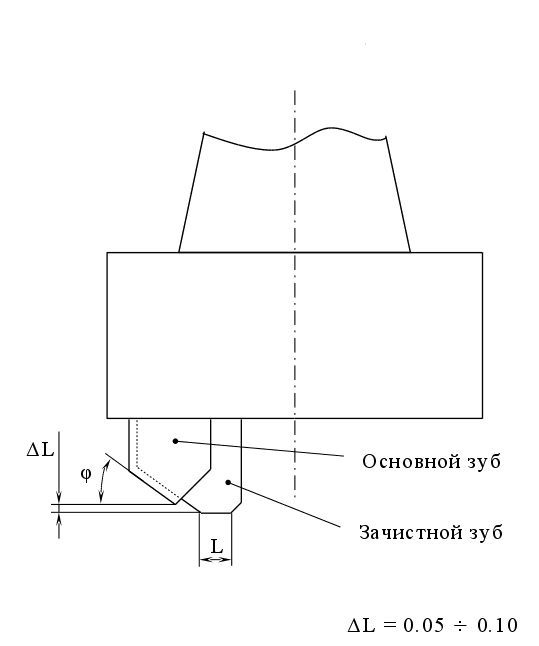
рис. 3.2 Конструкция фрезы с зачистным зубом
3.2. Прогнозирование точности и качества при проектировании технологических процессов механической обработки.
3.2.1. Цель проведения исследования.
Цель данного исследования – разработка программного пакета, прогнозирования точности обработки деталей на металлообрабатывающих станках, для ПЭВМ.
3.2.2. Содержание исследования.
В процессе работы было проведено исследование точности обработки деталей на металлообрабатывающих станках и, согласно методике, разработан алгоритм , приведенный в графической части дипломного проекта (см. 090202.ДП.ТМС.1.1.3.13.18), работы программы. Опыты проводились на токарно-винторезном станке. Результаты исследования занесены в таблицу (табл. 3.2.1).
3.2.3. Методика анализа точности обработки партии деталей, с помощью кривых распределения.
Для того, чтобы изделие экономично выполняло свое служебное назначение, оно должно обладать необходимым для этого качеством. Качество продукции – совокупность свойств продукции, обуславливающих ее пригодность удовлетворять определенные потребности в соответствии с ее назначением (ГОСТ 15467-79).
К основным показателям качества изделия можно отнести безотказность функционирования, долговечность, точность сопряжений, уровень шума, безопасность, коэффициент полезного действия, удобство и простоту обслуживания, степень механизации и т.д.
Количественное значение показателей качества может устанавливаться либо на стадии разработки проектного задания как уровень, к которому необходимо стремиться при проектировании деталей, либо в процессе проектирования просчитывается как результат, полученный при разработке данной конструкции. Качество изделия складывается из качества деталей, его составляющих и качества соединения этих деталей. Одним из наиболее важных показателей качества деталей считают прочность их изготовления. Под точностью детали понимают степень ее приближения к геометрически правильному ее прототипу. По-видимому, под геометрически правильным прототипом можно представить деталь, которая, работая в узле в сопряжении с деталями также геометрически правильно выполненными, обеспечивает максимальную долговечность изделия.
Точность механической обработки деталей на станках – это степень соответствия реальной поверхности обработанной детали идеальной схеме обработки, положенной в основу данного метода. Точность обработки – понятие чисто технологическое, характеризующее каждый из методов обработки.
После обработки партии деталей на настроенном станке (например, в течении одной смены) производят выбор некоторого количества деталей для обмера. В примере, приведенном ниже, анализ точности обработки партии деталей будет выполнен по результатам обмера диаметра у 50 деталей, который в операционном эскизе задан =160.08 В пределах указанной выборки (50 шт.) наибольший диаметр был Xmax = 16.05 мм, наименьший Xmin = 15.89 мм. Разница между Xmax и Xmin = = 0.16 мм, есть поле рассеивания размеров выборки.
Для определения закона нормального распределения случайных величин (и последующего определения по нему вероятного процента брака) первоначально по результатам замеров строят кривую эмпирического распределения размеров и определяют ее характеристики X – среднеарифметический размер партии и - среднее квадратичное отклонение, которое определяется по следующим зависимостям
X = (x1m1+x2m2+…+xkmk)/n = 1/nximi ; (3.2.1.)
![]() = =((x1-x)2m1+...+(xk-x)2mk)/n (3.2.2.)
= =((x1-x)2m1+...+(xk-x)2mk)/n (3.2.2.)
где xi – размер в соответствующем интервале
n – количество деталей в выборке
mi–абсолютная частота попадания размера в соответствующий интервал
k – число интервалов, на которые разбито поле рассеивания размеров.
Число интервалов рекомендуется определять по следующей зависимости
5lg(n)k (3.2.3.)
В нашем примере k = 5lg (50) 8. Зная и k, определяют цену деления по оси x
Cu = /k (3.2.4.)
Для построения графиков эмпирического и теоретического распределения размеров, для выполнения расчетов по формулам (3.2.3) и (3.2.4) а так же для определения оценочных критериев выборки целесообразно составить таблицу, которая для нашего примера будет содержать следующие данные
Табл. 3.2.
Значения расчетных величин.
| № | интервалы размеров xi | mi | среднее значение | ti | zt | k | Nx | Nx` | Nx-1/x |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
1 | 15.89…15.91 | 2 | 15.9 | 2.29 | 0.029 | 0.85 | 2 | 0.849 | 1.51 |
2 | 15.89…15.91 | 2 | 15.92 | 1.71 | 0.092 | 2.64 | 4 | 3.489 | 0.511 |
3 | 15.89…15.91 | 6 | 15.94 | 1.14 | 0.208 | 5.95 | 10 | 9.439 | 0.561 |
4 | 15.89…15.91 | 10 | 15.96 | 0.57 | 0.339 | 9.64 | 20 | 19.08 | 0.921 |
5 | 15.89…15.91 | 12 | 15.98 | 0.00 | 0.399 | 11.4 | 32 | 30.48 | 1.521 |
6 | 15.89…15.91 | 8 | 16.00 | 0.57 | 0.339 | 9.69 | 40 | 40.17 | 0.169 |
7 | 15.89…15.91 | 7 | 16.02 | 1.14 | 0.208 | 5.95 | 46 | 46.12 | 0.881 |
8 | 15.89…15.91 | 3 | 16.04 | 1.71 | 0.093 | 2.64 | 50 | 48.80 | 1.2 |
Пользуясь данными таблицы (колонки 2 и 3), строим график эмпирического распределения (рис. 3.3). При этом точки, принадлежащие каждому интервалу размеров, на графике наносятся против середины соответствующего интервала.
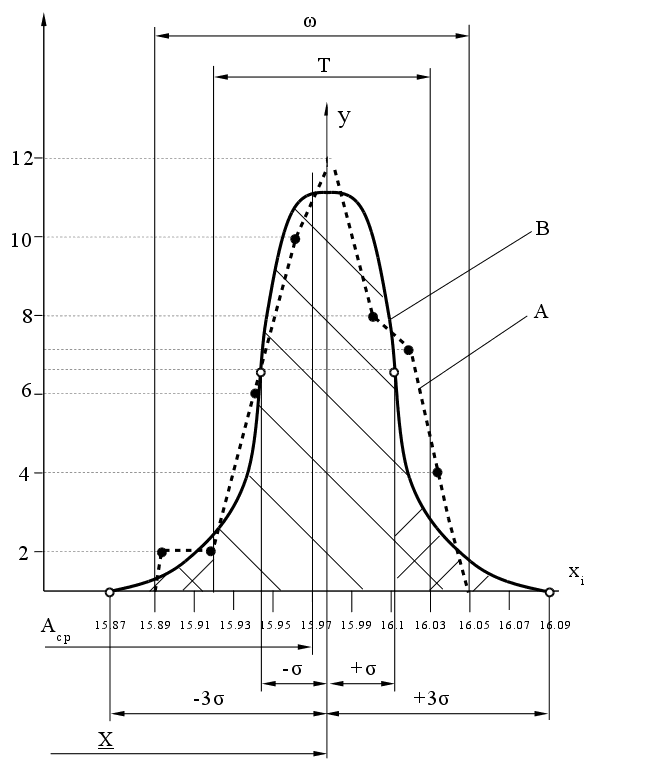
рис 3.3 График распределение размеров
На графике (см. рис. 3.3) измеренное поле рассевания размеров и допуск на изготовление Т. Пользуясь формулами вычислим характеристики эмпирического распределения.
Основной целью анализа распределения точности обработки партии деталей является прогнозирование вероятного количества бракованных и годных деталей на исследуемой операции. Выше было указано, что распределение размеров деталей на операциях механической обработки в большинстве случаев следует закону нормального распределения случайных величин. Это позволяет использовать указанный закон для анализа точности рассматриваемой операции. Для построения теоретической кривой нормального распределения (для последующего сравнения с эмпирической и установления возможности использования в расчетах закономерностей нормального распределения) используют следующую методику
Аналитически закон нормального распределения выражается уравнением
![]()
y = 1/(o2) e^(-(x-xo)2/2o2) (3.2.5.)
где e – основание натуральных логарифмов
x и о – параметры генеральной совокупности.
Под генеральной совокупностью следует понимать все количество деталей, которое будет выполнено по данному технологическому процессу. Для использования закона нормального распределения к анализу точности обработки партии деталей с некоторой погрешностью приравнивают соответствующий параметры экспериментального распределения и генеральной совокупности о xo = xo.
Для практических расчетов при n20 целесообразно использовать более точное соотношение с учетом погрешности эмпирических параметров распределния
![]() о
=
2
(3.2.6.)
о
=
2
(3.2.6.)
![]() xo
= x
n (3.2.7.)
xo
= x
n (3.2.7.)
С учетом использования экспериментальных данных полагают
y![]() = K`/(nCu)
= 1/(o2)
e^(-(x-xo)2/2o2) (3.2.8.)
= K`/(nCu)
= 1/(o2)
e^(-(x-xo)2/2o2) (3.2.8.)
где K` - теоретическая частота для любых значений x=m;
Cu – величина интервала по оси абсцисс.
Из (3.2.8) получаем
K` = nCu / o (3.2.9.)
t = (x-xo)/o (3.2.9.)
K![]() `
= nCu/o
1/2
e^(-(x-xo)2/2o2) (3.2.9.)
`
= nCu/o
1/2
e^(-(x-xo)2/2o2) (3.2.9.)
В математической статистике для проверки нормальности распределения выборки используется несколько критериев. Наиболее простым для вычисления является критерий академика А.Н.Колмогорова - .
Используем этот критерий для анализа нормальности распределения приведенной выше выборки.
Первоначально делается предположение о том, что партия деталей, из которой извлечена выборка, имеет нормальное распределение, следовательно, равенства (1) и (2) справедливы. Согласно методике
![]()
= (Nx
– N`xmax)/n (3.2.10)
= (Nx
– N`xmax)/n (3.2.10)
где N = mi – накопленные эмпирические частоты распределения случайной величины xi, которые подсчитываются в нашем примере по данным таблицы (табл.5.1 столбец 3).
Nx` - накопленные теоретические частоты распределения.
В числителе формулы (3.2.1) берется наибольшая абсолютная разность накопленных теоретических и эмпирических частот. Накопленные теоретические частоты подсчитываются на основе формулы (3.2.2).
- случайная величина, которая подчиняется нормальному закону распределения, по которому можно вычислить вероятность этой величины P().
Р() – выражает вероятность соответствия эмпирического распределения, полученного в примере, распределению генеральной совокупности. Для анализа распределений, рассматриваемых в технике, установлено, что если Р() g (3.2.11.)
где g – некоторое критическое значение критерия .
В связи с тем, что рассеивание размеров на исследуемой операции подчиняется закону нормального распределения, следовательно, практически размеры деталей могут находиться в пределах поля, ограниченного теоретической кривой. Годными же будут детали, размеры которых остаются в пределах поля допуска. (рис.3.2)
Вероятность получения количества деталей в пределах поля допуска равна отношению площади, заключенной между ординатами, проведенными через границу поля допуска и границы теоретической кривой. Для определения площади используют нормированную функцию Лапласа, которая получается после интегрирования уравнения кривой Гаусса, с использованием подстановки
t = (x-xo) / o (3.2.12.)
Значения функции Лапласа табулированы. В приведенном виде формула используется для определения половины площади под кривой, так как при t , Ф(t) стремится к 0.5. Для практических расчетов используют диапазон кривой Гаусса в пределах –3
Похожие работы
... использования материала.4. ОРГАНИЗАЦИЯ ПРОИЗВОДСТВА 4.1. Состав продукции цеха, регламент его работы и характеристика. Приспособление для восстановления внутренних поверхностей деталей выпускает специальный цех, специализированный на производстве приспособлений и инструментов для восстановления поверхностей деталей электромеханической обработкой. Цех работает в две рабочих смены, рабочих часов в ...
... работник, и автоматизированные, где контроль за безопасной работой и режимом тепловой обработки обеспечивает сам тепловой аппарат при помощи приборов автоматики. На предприятиях общественного питания тепловое оборудование может использоваться как несекционное или секционное, модулированное. Несекционное оборудование, это оборудование, которое различно по габаритам, конструктивному исполнению и ...
0 комментариев