Навигация
1. Теорема линейности.
Если x(nT) = ax1(nT) + bx2(nT) ,
то X(Z) = a X1(Z) + bX2(Z).
Теорема запаздывания.
Если x(nT) = x1(nT - QT) ,
то X(Z) = X1(Z) Z-Q.
Теорема о свертке сигналов.
Если X(nT) = ![]() x1(kT) x2(nT - kT) ,
x1(kT) x2(nT - kT) ,
то X(Z) = X1(Z) X2(Z).
Теорема об умножении сигналов.
Если x(nT) = x1(nT) x2(nT) ,
то X(Z) = ![]() X1(V) X2(
X1(V) X2(![]() ) V-1 dV,
) V-1 dV,
где V, Z - переменные на плоскости Z.
Теорема энергий (равенство Парсеваля).
![]() x2(nT) =
x2(nT) =![]() X(Z) X(Z-1) Z-1 dZ.
X(Z) X(Z-1) Z-1 dZ.
Z - преобразование дискретных сигналов имеет значение равное значению преобразования Лапласа непрерывных сигналов.
Дискретное преобразование Фурье.
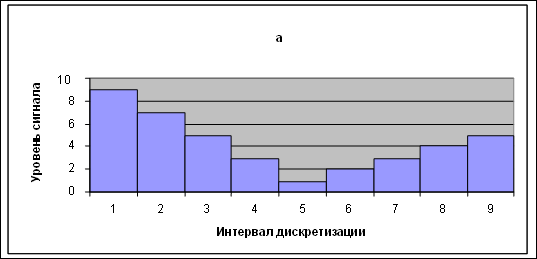
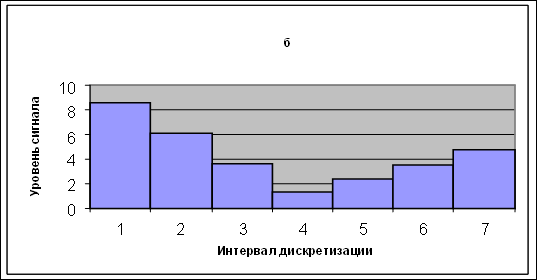
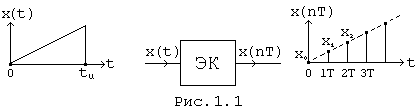
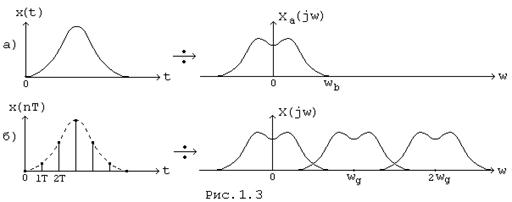
Если сигнал ограничен во времени значением tu , а его спектр - частотой wв , то он полностью характеризуется конечным числом отсчетов N как во временной, так и в частотной областях (Рис. 1.7, а, б) :
N = tu/T - во временной области, где T = 1/fд ,
N = fд/f1 - в частотной области, где f1 = 1/tu .

Дискретному сигналу соответствует периодический спектр, дискретному спектру будет соответствовать периодический сигнал. В этом случае отсчеты X(nT) = {X0 ; X1 ; … XN-1} являются коэффициентами ряда Фурье периодической последовательности X(jkw1), период, который равен wд. Соответственно, отчеты X(jkw1) = {X0 ; X1 ; … XN-1} являются коэффициентами ряда Фурье периодической последовательности X(nT), период, который равен tu.
Связь отсчетов сигнала и спектра устанавливается формулами дискретного преобразования Фурье (ДПФ). Формулы ДПФ следуют из формул Фурье для дискретных сигналов (1.5), если непрерывную переменную w заменить дискретной переменной kw1, то есть
w ® kw1 , dw ® w1.
После замены переменной в (1.5) получим
X(jkw1) = ![]() x(nT)
x(nT)![]() ,
,
x(nT) =![]()
![]() X(jkw1)
X(jkw1)![]() .
.
Отсюда после подстановки w1 = wд/N, T = 2p/wд формулы ДПФ принимают окончательный вид
X(jkw1) =![]() x(nT)
x(nT)![]() - прямое ДПФ ,
- прямое ДПФ ,
x(nT) =![]() X(jkw1)
X(jkw1)![]() - обратное ДПФ (1.10)
- обратное ДПФ (1.10)
Сигнал с ограниченным спектром имеет, строго говоря, бесконечную протяженность во времени и, соответственно бесконечное число отсчетов и непрерывный спектр. Спектр останется непрерывным, если число отсчетов сигнала ограничить конечным числом N. Формулы (1.10) в этом случае будут выражать связь между N отсчетами дискретного сигнала и N отсчетами его непрерывного спектра, который можно полностью восстановить по его отсчетам.
Пример. Определить отсчеты спектра сигнала на Рис. 1.5, а.
Здесь N = 2 поэтому X(jkw1) =![]() x(nT) e-jpkn следовательно
x(nT) e-jpkn следовательно
X(j0w1) =![]() x(nT)e-j0 = x(0T) + x(1T) = a + b
x(nT)e-j0 = x(0T) + x(1T) = a + b
X(j1w1) =![]() x(nT)e-jpn = x(0T) e-j0 + x(1T) e-jp = a - b
x(nT)e-jpn = x(0T) e-j0 + x(1T) e-jp = a - b
график отсчетов спектра приведен на Рис. 1.5, б, где w1 = wд/N = 0,5wд.
Сигнал с конечным числом отсчетов N имеет спектр, который повторяет с конечной погрешностью спектр сигнала с бесконечным числом отсчетов : спектры совпадают на отсчетных частотах kw1 и отличаются на других частотах. Отличие спектров тем меньше, чем больше N. В самом деле, реальные сигналы обладают конечной энергией и, следовательно, начиная с некоторого номера отсчета остальными номерами можно пренебречь ввиду их малости, что не окажет заметного влияния на спектр сигнала.
Пример. Осуществить дискретизацию экспоненциального импульса X(t) = Ae-at = 1 e-10t и сравнить спектры исходного и дискретного сигналов.
Решение.
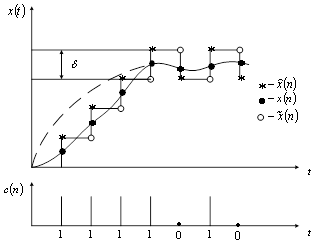
График сигнала X(t) представлен на Рис. 1.8

Пусть T = 0,02с. В этом случае плавным соединением отсчетов сигнала (штриховая линия на Рис. 1.8) сигнал восстанавливается удовлетворительно хотя заметны искажения в окрестности точки t = 0, поэтому ошибки наложения будут некоторым образом влиять на спектральные характеристики.
Пусть tu = 0,4с. В этом случае
N = tu/T = 20.
Расчет спектра по формуле прямого ДПФ в точке w = 0 (k = 0) запишется так
X(j0w1) = 1,0 + 0,8187 + 0,6703 + 05488 + 0,4493 + 0,368 + 0,3012 + 0,2466 + 0,2019 + 0,1653 + 0,1353 + 0,1108 + 0,09072 + 0,07427 + 0,06081 + 0,04979 + 0,04076 + 0,03337 + 0,02732 + 0,02237 = 5,41
Истинное значение спектра в точке w = 0 можно определить зная спектр аналогового экспоненциального импульса
Xa(jw) =![]() , следовательно Xa(j0) =
, следовательно Xa(j0) =![]() = 0,1.
= 0,1.
чтобы сравнить спектры дискретного и непрерывного сигналов, дискретный спектр необходимо денормировать умножением на T, так как формулы Фурье для дискретных сигналов применяются в нормированном виде. Поэтому
X(jow1) = 5,41 T = 5,42Ч0,02 = 0,1082.
Таким образом совпадение спектров Xa(jw) и X(jw) в точке w = 0 вполне удовлетворительное. Некоторая неточность объясняется влиянием ошибок наложения.
Уместно заметить, что выбор шага дискретизации достаточно контролировать в точках максимальной крутизны исходной функции X(t). В рассмотренном примере такой точкой является момент времени t = 0.
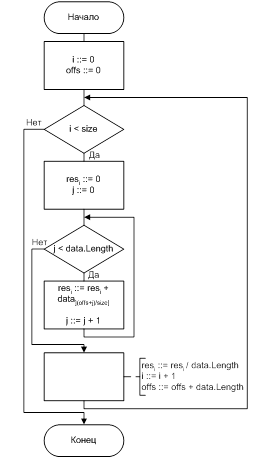
В заключение отметим, что формулы ДПФ упрощают расчетные процедуры по взаимному преобразованию сигналов и их спектров, что особенно важно для технических систем, функционирующих В реальном масштабе времени. В этих случаях применяется алгоритм быстрого преобразования Фурье (БПФ), основанный на формулах ДПФ. Ускоренная процедура расчетов по алгоритму БПФ достигается за счет исключения повторных арифметических операций, характерных для расчетов по формулам ДПФ.
Похожие работы
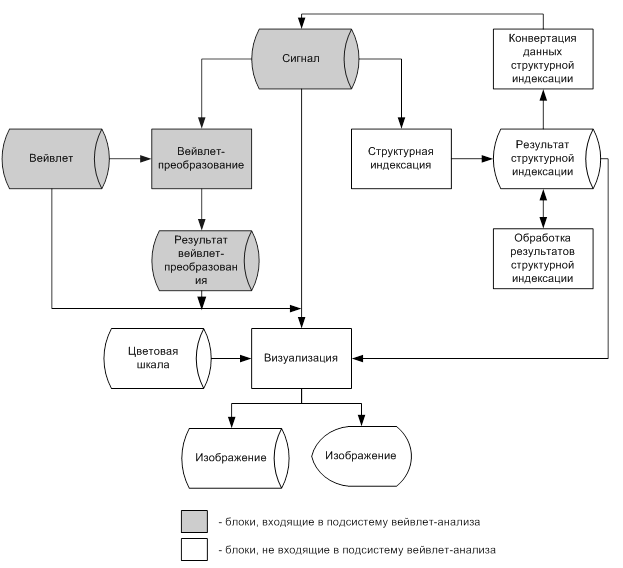
... для выявления нестационарных составляющих сигнала, что крайне полезно при подборе способов фильтрования сигнала с помощью структурной индексации. В результате построения подсистемы вейвлет-анализа система многомасштабного анализа дискретных сигналов (МАДС) дополнит свои функциональные возможности способностью выделения из исходного сигнала наиболее четких его составляющих, что должно быть учтено ...
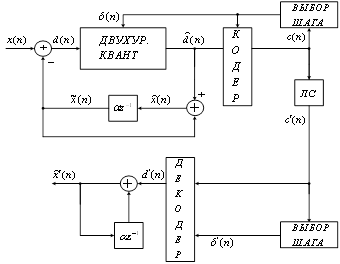
... сигналов. При этом необходимо на блоке отсчетов определять оптимальный порядок предсказателя и коэффициенты предсказания . Адаптация предсказателя может осуществляться по входному или выходному сигналу. Структурная схема системы АРИКМ с адаптивным предсказанием изображена на рисунке (рисунок 9). При адаптации по входу для восстановления сигнала в приемнике необходимо передавать , и . Пусть ...
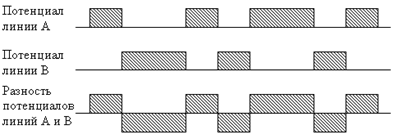
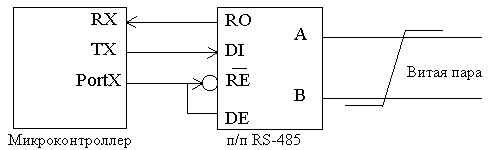
... количества байтов данных и данные для записи в регистры. Поле данных может не существовать (иметь нулевую длину) в определенных типах сообщений. В MODBUS – сетях используются два метода контроля ошибок передачи. Содержание поля контрольной суммы зависит от выбранного способа передачи. ASCII Когда используется ASCII-режим поле контрольной суммы содержит два ASCII-символа. Контрольная сумма ...
... кодовыми словами конечной размерности (ошибки квантования). Поэтому сигнал на выходе цифровой цепи отличается от идеального варианта на величину погрешности квантования. Цифровая техника позволяет получить высокое качество обработки сигналов несмотря на ошибки квантования: ошибки (шумы) квантования можно привести в норму увеличением разрядности кодовых слов. Рациональные способы конструирования ...

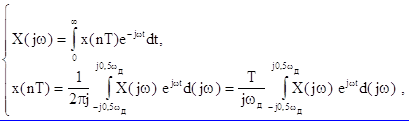
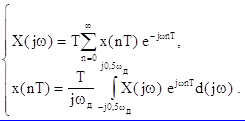
0 комментариев