Fm 3Fm f
X(t)
Ba(t)=Bб(t) ( т.к. скорости изменения одинаковы )
Восстановление и демонстрация цифровых изображений
Свойства системы зрения человека
Некоторые замечания о сокращении избыточности изображений
Схемы сокращения избыточности изображений с обработкой в пространственной области
Схемы сокращения избыточности изображений с обработкой в области преобразований
Отсчета
Повышение резкости изображений
Основные методы повышения резкости изображений
Повышение резкости изображения «вслепую» и методом уравнивания энергетических спектров
Замечания о восстановлении изображений в яркостной и плотностной областях
Повышение резкости изображений с характеристиками
Воспроизведение изображений по проекциям
Методы воспроизведения изображений
Повышение качества изображений
Навигация
Методы воспроизведения изображений
Дискретизация и квантование изображений
133817
знаков
3
таблицы
9
изображений
4.5.2. Методы воспроизведения изображений
Основная операция при воспроизведении изображения по проекциям следует из теоремы о проекции и сечении. Преобразование Фурье от проекции дает значения преобразования Фурье от исходного распределения вещества в некотором его сечении. Если получить достаточно плотный набор таких сечений, то все пространство спектров будет заполнено сечениями и с помощью обратного преобразования Фурье можно завершить процесс воспроизведения изображения.
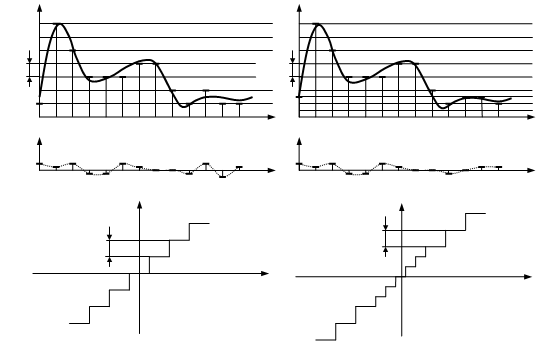
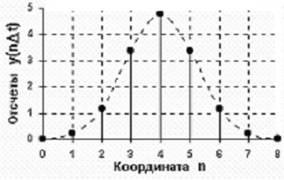
Рис. 4.21. Отсчеты в пространстве преобразований Фурье, полученные из набора проекций.
Каждая точка представляет значение F(w1,w2), полученное вычислением ДПФ проекции g(u) под углом 
.
Эта операция достаточно просто описывается, но для фактического ее выполнения необходимы весьма сложные и трудоемкие исследования. При воспроизведении изображения на основе сечений спектра важными являются следующие положения:
1. При вращении источника плоского луча для каждого из углов получается своя проекция. Число проекций, необходимых для достаточно полного заполнения пространства преобразований Фурье, очевидно, зависит от формы преобразования Фурье воспроизводимого распределения. Однако чем меньше шаг по углу, тем плотнее заполняется пространство спектров (см. рис. 4.21). На практике число проекций ограничивается двумя факторами: 1) увеличением объема вычислений, связанным с обработкой дополнительных проекций; 2) увеличением дозы облучения при получении дополнительных проекций (что очень важно в медицинских приложениях метода).
2. Сечения спектрального пространства образуют равномерную сетку в той системе координат, где на одной из осей откладывается угол поворота 
. Однако размещение отсчетов спектра в каждом из сечений не согласуется с обычными двумерными преобразованиями. Двумерное ДПФ вычисляется на прямоугольной сетке отсчетов, образующих строки и столбцы, а точки, в которых известны ДПФ сечений, образуют полярный растр, показанный на рис. 4.21. Поэтому необходимо с помощью интерполяции перейти к прямоугольному растру, что несложно с точки зрения теории, но нетривиально на практике, поскольку каждый отсчет, находящийся на концентрической полярной сетке, перед интерполяцией необходимо перевести в соответствующую прямоугольную систему координат. Такое преобразование двумерных координат и интерполяцию можно несколько упростить, пользуясь методом так называемого копцентрично - прямоугольного растра, но зато при этом интервалы дискретизации будут не одинаковыми [50].
3. Как видно из рис. 4.21, двумерное пространство преобразований Фурье очень плотно заполняется в области низких частот, а высокие частоты представлены гораздо реже. Поэтому для воспроизведения крупноструктурных элементов, описываемых низкочастотным спектром, требуется небольшое число проекций, например 20—30. Для достаточно четкого представления высокочастотных составляющих необходимо большое число проекций (100 и более). Если число проекций ограничено, то можно воспользоваться имеющимися проекциями и более плотно заполнить пространство спектров путем интерполяции. Это несколько улучшает результаты воспроизведения, но возможности данного метода ограничены, поскольку результаты интерполяции могут не соответствовать реальным значениям спектров. Качество и детали изображения определяются именно теми спектральными составляющими, которые нельзя предсказать путем интерполяции.
Другой метод воспроизведения изображений, в котором применяется цифровая обработка сигналов, называется методом свертки или «размазывания». Для пояснения метода рассмотрим две взаимно перпендикулярные проекции. Если каждую из проекций «размазать» (т.е. образовать двумерную функцию, не изменяющуюся по одной оси и совпадающую с исходной одномерной проекцией по второй оси) и значения обеих функций сложить как ортогональные векторы, то получится очень грубая аппроксимация исходного объекта. Читатель может проверить это, взяв для примера квадрат и построив проекции в направлениях, перпендикулярных его сторонам. В общем представляется возможным получить изображение «размазывая» проекции (это можно сделать путем свертки с подходящей функцией) и образуя сумму после соответствующего взвешивания отдельных слагаемых. Такой метод можно реализовать с помощью цифровой обработки, а также оптическими средствами. Однако данный метод крайне чувствителен к помехам, поскольку операции свертки и взвешивания влияют на обрабатываемые сигналы примерно так же, как дифференцирование.
Как образец результатов, получаемых при воспроизведении изображений цифровыми методами, на рис. 4.22 показано сечение человеческого мозга, полученное с помощью серийного рентгеновского аппарата для воспроизведения изображений внутреннего строения головы.
Этот краткий обзор не исчерпывает всех вопросов, связанных с воспроизведением изображений на основе проекций. С другими методами можно познакомиться по работам, указанным в списке литературы, составленном Мерсеро и Оппенгеймом [50].
Похожие работы
... сигнала уровень квантования называют также глубиной дискретизации или битностью. Глубина дискретизации измеряется в битах и обозначает количество бит, выражающих амплитуду сигнала. Чем больше глубина дискретизации, тем точнее цифровой сигнал соответствует аналоговому. В случае однородного квантования глубину дискретизации называют также динамическим диапазоном и измеряют в децибелах (1 бит ≈ ...
... иметь дело с данными, имеющими конечный размер, – например, с массивами чисел конечного размера и ограниченной разрядности. Рассмотренная выше теорема дискретизации дает такую возможность. Количество информации, энтропия источника сообщений Для сравнения между собой различных источников сообщений необходимо ввести некоторую количественную меру, которая дала бы возможность объективно ...
... функций в виде зависимости их значений от определенных аргументов Δвремени, линейной или пространственной координаты и т.п.) при анализе и обработке данных широко используется математическое описание сигналов по аргументам, обратным аргументам динамического представления. Так, например, для времени обратным аргументом является частота. Возможность такого описания определяется тем, что любой ...
... рисунков в формате А0-А1 со скоростью 10-30 мм/с. Фотонаборный аппарат Фотонаборный аппарат можно увидеть только в солидной полиграфической фирме. Он отличается своим высоким разрешением. Для обработки информации фотонаборный аппарат оборудуется процессором растрового изображения RIP, который функционирует как интерпретатор PostScript в растровое изображение. В отличие от лазерного принтера в ...
0 комментариев