Схемы сокращения избыточности изображений с обработкой в области преобразований

4.3.3. Схемы сокращения избыточности изображений с обработкой в области преобразований

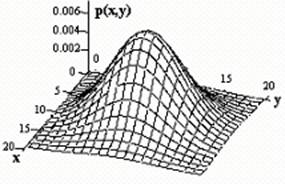
Для пояснения основных операций, выполняемых системой сжатия видеоинформации с обработкой в области преобразований, обратимся к ковариационной матрице, определяемой соотношением (4.20). Матрица [C_g] описывает корреляцию отсчетов изображения в плоскости (х, у), являющейся координатной плоскостью изображения. Важным методом многомерного статистического анализа служит исследование массива данных не только в их естественных координатах, но и в системах координат с более удобными свойствами. В частности, весьма полезными оказались системы координат, основанные на собственных значениях и собственных векторах ковариационной матрицы

[ C_g ] = [ Ф ] [ ] [ Ф ]^T= 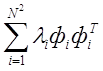, (4.24)

где [Ф] - матрица, составленная из ортогональных собственных вектор - столбцов Ф_i а [] - диагональная матрица собственных значений.

Преобразование координат, определяемое матрицей собственных векторов [Ф], обладает тем свойством, что оно производит преобразование заданного массива чисел в другой с некоррелированными элементами, причем получающиеся компоненты имеют убывающие дисперсии. Пусть собственные значения матрицы [C_g] расставлены в убывающем порядке и пронумерованы так, что

, (4.25)

и пусть собственные векторы, связанные с ними, расставлены в том же порядке. Тогда матрица собственных векторов [Ф] обладает тем свойством, что умножение ее на вектор-изображение g (образованный лексикографической расстановкой) дает вектор

G = [ Ф ]g , (4.26)

имеющий некоррелированные компоненты, причем компоненты вектора G оказываются расставленными в порядке убывания их дисперсий [29], что является свойством дискретного варианта разложения Карунена - Лоэва, фактически описанного соотношениями (4.24) - (4.26).

Полезность преобразования Карунена — Лоэва ( КЛ, или ковариационного) для сокращения избыточности изображений очевидна. Массив отсчетов изображения заменяется набором переменных, имеющих различные статистические веса ). Сжатие можно получить, отбрасывая переменные с малым статистическим весом и сохраняя остальные. Если, например, оставить M<N² компонент вектора G и передать их вместе со специальной информацией о том, какие компоненты сохранены, то можно сузить ширину полосы в N²/M раз. В приемнике из принятых М чисел образуют N² - компонентный вектор путем подстановки нулей вместо N²-М непереданных компонент. Из этого нового вектора, обозначенного как G' , с помощью преобразования

 g_c = [ Ф ]^TG’ (4.27)

восстанавливается исходное изображение. В процессе сжатия возникает средняя квадратическая ошибка

|| g - g_c || =  (4.28)

особенность КЛ - преобразования состоит в том, что из всех линейных преобразований именно оно обеспечивает минимальную величину этой ошибки.

Из соотношений (4.25) и (4.26) видно, что число операций, необходимых для выполнения КЛ - преобразования, пропорционально N⁴, так как исходный массив содержит N² отсчетов. Для типичных значений N ( N = 256 или 512 ) такое число чрезмерно велико. Еще труднее вычислить собственные значения и собственные векторы ковариационной матрицы [C_g] размером N²N² Эксперименты показал, что очень многие элементы этой матрицы близки к нулю, т.е. коэффициент корреляции между отсчетами быстро стремится к нулю с увеличением расстояния между соответствующими точками изображений. Расстояние, при котором коэффициент корреляции между яркостями элементов изображения становится настолько малым, что его можно приравнять нулю (например, 5 или 10 % максимального значения), называется радиусом корреляции отсчетов; его можно выразить через целое число отсчетов. Зная это расстояние, все изображение можно разбить на блоки, размер которых больше радиуса корреляции, но сравним с ним. Если размер каждого блока равен Р, то можно вычислить. ковариационную матрицу всех блоков, имеющую размер P²P²:

 [C_gp] = 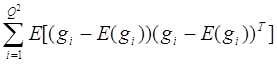, (4.29)

где Q=N/P, a g_i- вектор, построенный из отсчетов i-го блока. Тогда, если [Ф_p] - матрица собственных векторов, связанных с P² собственными значениями, расположенными так же, как в формуле (4.25), то операции по сокращению избыточности для каждого из блоков выполняются по формулам (4.26) и (4.27),. как для полного изображения, но матрица [Ф] заменяется на [Ф_p]. Как правило, радиус корреляции большинства изображений имеет такую величину, что Р=16 является разумным компромиссом между размером ковариационной матрицы и скоростью, с которой коэффициент корреляции отсчетов приближается к нулю [30]. Длительность вычислений, выполняемых при сжатии видеоинформации поблочно, пропорциональна Q²/P⁴.

Хотя разложение изображения на блоки и делает сжатие видеоинформации методом КЛ - преобразования реально осуществимым процессом, но эффективность его остается недостаточной. Большой объем вычислений препятствует использованию подобных методов для обработки изображений типа телевизионных.

Создание алгоритмов быстрых преобразований (Фурье, Адамара и т.д.) существенно повлияло на многие области применения цифровой обработки сигналов. Аналогичным образом оно - сказалось и на методах сокращения избыточности изображений. Любое линейное преобразование, подобное разложению Карунена - Лоэва, переводит изображение в новую систему координат. В силу свойств КЛ - преобразования случайные компоненты изображения в новых координатах оказываются некоррелированными. Резонно спросить: будут ли другие преобразования, особенно быстрые типа БПФ, обладать такими же полезными свойствами? К счастью, ответ оказывается положительным. Хотя быстрые преобразования и не приводят к полной некоррелированности компонент, как в случае КЛ - преобразования, но все же они дают очень хорошие результаты. Их достоинства, связанные с быстротой вычислений, полностью компенсируют некоторое понижение эффективности сжатия, характерное для них.

Схемы сжатия на основе быстрых преобразований можно описать примерно так же, как и схемы с КЛ - преобразованием. Дополнительным достоинством быстрых алгоритмов является их разделимость, так что двумерные преобразования можно выполнить с 'помощью одномерных операций. Кроме того, их проще описать математически. Если матрица [W] соответствует оператору ортогонального унитарного одномерного преобразования (как, например, матрицы ядер преобразований Фурье, Адамара и т.д. [31] ), то «поворот» изображения в новую систему координат выполняется по формуле

[ G ] = [ W ]^T [ g ] [ W ] , (4.30)

гдe ,[g] - исходная матрица отсчетов изображения размером NN, a [G] - преобразование матрицы [g]. Нетрудно заметить, что формула (4.30) описывает двухэтапное преобразование: сначала по строкам изображения, а затем по столбцам преобразований от строк. Записывая преобразование (4.30) в явном виде через элементы матриц, получим:

G(m,n) =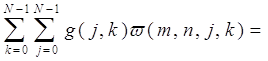

 (4.31)

=  

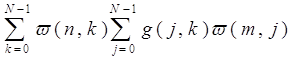
где второе равенство является следствием разделимости ядра преобразования. Свойством разделимости обладает ядро преобразования Фурье, наиболее часто применяемого на практике:

  (m,n,j,k) = exp [- ] =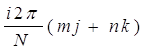

(4.32)

= exp [ -  ] exp [ -  ] ,

а также ядра менее известных преобразований, таких, как преобразования Адамара и Хаара. Более подробно этот вопрос рассмотрен в работе Эндрюса [31].

Собственные значения _i , получаемые методом КЛ - преобразования, соответствуют фактическим величинам дисперсий проекций вектора-изображения на координатные оси пространства, в котором вñå компоненты изображения некоррелированы. В системах координат, получаемых при быстром преобразовании, коэффициенты преобразования (т.е. элементы матрицы [G] ) равны проекциям вектора - изображения на оси координат, полученным с помощью матрицы преобразования [W], но не являются дисперсиями. Однако как при КЛ - преобразовании, так и в пространствах быстрых преобразований происходит концентрация энергии. В первом случае наибольшие

дисперсии (и, следовательно, наибольшие энергии) связаны с теми столбцами матрицы [Ф] или [Ф_р], которые соответствуют предпочтительным (или «естественным») направлениям наибольшего изменения видеоинформации. Аналогично в пространстве быстрого преобразования наибольшими являются коэффициенты, которые соответствуют предпочтительным (или «естественным») направлениям вектора-изображения. С этой точки зрения сжатие в пространстве преобразований (как для преобразования Карунена - Лоэва, так и для быстрых преобразований) является по существу разложением изображения в ряд по базисным векторам (или базисным изображениям, так как каждый вектор должен описывать двумерную структуру) и таким усечением разложения, при котором ошибка мала, а число отбрасываемых составляющих - большое. Усечение оказывается возможным потому, что небольшое число компонент содержит основную часть энергии изображения.

Для иллюстрации рассмотрим схему сжатия в пространстве-преобразовании, основанную на преобразовании Фурье. Из соотношений (4.31) и (4.32) видно, что (т, п)-й коэффициент преобразования G(m,n) является проекцией исходного изображения g(j,k) на базисный вектор (или базисное изображение), образованный при помощи (т, п)-_го  значения ядра Фурье

( m , n) = exp ( ) . (4.33)

Для типичных изображений характерно, что в области пространственных частот элементы с малыми индексами велики по сравнению с элементами с большими индексами. Таким образом, структура изображения обычно имеет низкочастотный характер. Низкочастотные составляющие определяют контуры предметов, а также яркость и контрастность изображения. Высокочастотные - составляющие создают резкие линии и определяют общую четкость изображения, но суммарная энергия их невелика. Так, 95% энергии типичного изображения может приходиться на низкочастотные составляющие, занимающие 5% от общей площади двумерной пространственно - частотной области преобразования Фурье. Сохраняя эти спектральные составляющие и достаточно много высокочастотных компонент, чтобы резкость изображения была приемлема для человеческого глаза, можно добиться существенного уменьшения объема избыточной информации.

После того как установлено, что основной принцип сжатия в пространстве преобразований заключается в избирательном сохранении коэффициентов разложения, задача создания системы сжатия изображений может показаться нетрудной. Сложность построения подобных схем кодирования обусловлена необходимостью сравнения свойств операторов различных преобразований и создания методов выбора коэффициентов преобразования, которые следует оставить. Кроме того, задача усложняется квантованием выбранных коэффициентов и кодированием квантованных чисел. Ниже приведены краткие результаты исследований, посвященных этим вопросам.

Был исследован ряд алгоритмов быстрого преобразования, таких, как преобразования Фурье, Адамара, Xaapa [32], слэнт - преобразование [33], косинусное преобразование [34], преобразование по дискретно - линейному базису [35]. Все алгоритмы сравнивались по эффективности сжатия с преобразованием Карунена - Лоэва (оптимальным). Для выявления оптимального алгоритма необходимо сравнивать все преобразования в одинаковых условиях - при одном и том же входном изображении и одинаковых параметрах схем выбора, квантования и кодирования коэффициентов. Этого не было сделано, но приводимые в литературе данные позволяют сделать следующие выводы.

1. Ни один из алгоритмов быстрого преобразования не обеспечивает оптимальной эффективности сжатия изображения, какая получается (при использовании преобразования Карунена - Лоэва.

2. По таким критериям качества, как средняя квадратическая ошибка, ближайшим к преобразованию Карунена - Лоэва, оказывается слэнт - преобразование, а за ним следуют по порядку преобразования Фурье, Адамара и Хаара, причем сравнение выполнялось для изображений небольшого формата, например 1616 или 32

Похожие работы

Дискретизация сигнала

Скачать

16809

0

4

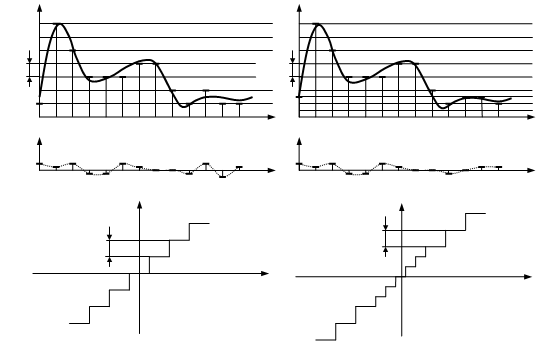
... сигнала уровень квантования называют также глубиной дискретизации или битностью. Глубина дискретизации измеряется в битах и обозначает количество бит, выражающих амплитуду сигнала. Чем больше глубина дискретизации, тем точнее цифровой сигнал соответствует аналоговому. В случае однородного квантования глубину дискретизации называют также динамическим диапазоном и измеряют в децибелах (1 бит ≈ ...

Квантование сообщений. Ошибки квантования. Энтропия источника сообщений

Скачать

14053

0

1

... иметь дело с данными, имеющими конечный размер, – например, с массивами чисел конечного размера и ограниченной разрядности. Рассмотренная выше теорема дискретизации дает такую возможность.   Количество информации, энтропия источника сообщений Для сравнения между собой различных источников сообщений необходимо ввести некоторую количественную меру, которая дала бы возможность объективно ...

Описание сигналов

Скачать

23730

0

8

... функций в виде зависимости их значений от определенных аргументов Δвремени, линейной или пространственной координаты и т.п.) при анализе и обработке данных широко используется математическое описание сигналов по аргументам, обратным аргументам динамического представления. Так, например, для времени обратным аргументом является частота. Возможность такого описания определяется тем, что любой ...

Автоматизированные системы обработки информации и управления

Скачать

326231

12

0

... рисунков в формате А0-А1 со скоростью 10-30 мм/с. Фотонаборный аппарат Фотонаборный аппарат можно увидеть только в солидной полиграфической фирме. Он отличается своим высоким разрешением. Для обработки информации фотонаборный аппарат оборудуется процессором растрового изображения RIP, который функционирует как интерпретатор PostScript в растровое изображение. В отличие от лазерного принтера в ...