Fm 3Fm f
X(t)
Ba(t)=Bб(t) ( т.к. скорости изменения одинаковы )
Восстановление и демонстрация цифровых изображений
Свойства системы зрения человека
Некоторые замечания о сокращении избыточности изображений
Схемы сокращения избыточности изображений с обработкой в пространственной области
Схемы сокращения избыточности изображений с обработкой в области преобразований
Отсчета
Повышение резкости изображений
Основные методы повышения резкости изображений
Повышение резкости изображения «вслепую» и методом уравнивания энергетических спектров
Замечания о восстановлении изображений в яркостной и плотностной областях
Повышение резкости изображений с характеристиками
Воспроизведение изображений по проекциям
Методы воспроизведения изображений
Повышение качества изображений
Навигация
X(t)
Дискретизация и квантование изображений
133817
знаков
3
таблицы
9
изображений
0 x(t)
x(t)=Re{x(t)}=E(t)cosy(t)
`
Нам нужно установить правило выбора сомножителей E(t) и cos(y(t)) т.к.
если мы узнаем один , то легко найдем другой .
Понятие огибающей очень расплывчато , поясним это на примерах :
( ) -огибающие для одного процесса
разные .
Первый дал понятие огибающей и фазе Гильберт , он дал определение
мнимой составляющей ( т.е. ввел комплексные величины ) .
Ґ
(t)=1/p тxi(t )/ t-t dt
Пара преобразований -Ґ
Гильберта Ґ
x(t)=1/p т h(t)/ t-t. dt
-Ґ
Преобразование Гильберта - широкополосный фазовращатель , оно
поворачивает все спектральные составляющие на 90° .
ѕѕѕѕѕ
E(t)= Ц x(t) + h(t) - огибающая понятия применимые
для любого сигнала .
y(t)=arctg[
(t)/ x(t)] - фаза
w(t)=dy(t) - частота
dt
x(t)=Acosw t ; h(t)=Asinw t ( т.е. h(t) получается приповороте x(t)
на 90° ).
x(t)= Acosw t +Asinw t = A
Схема получения АМ ОБП .
l
1/2cos(w -l)t+1/2cos(w +l )t
 | |||
 | |||
x(t) x(t)cosw t
генератор
cosw t
cos(w - l)t
+
j=p/2 j=p/2
sinlt sinw t h(t)sinw t
1\2cos(w
- l)t- 1/2cos(w +l)t
+ Получили АМ ОБП без использования фильтров .
Мы оперируем комплексными функциями для того
чтобы убрать основную часть энергии несущей .
Огибающие и фаза УПСП (узко-полосного случайного процесса ).
Квадратурные составляющие огибающей .
Dw<<w
460 465 470 f,кГц
y(t) = w0t- j(t)
w0 - ( ) j(t)
y(t)- ( )
t t
Фаза УПСП разбивается на две составляющие флуктуированную j(t)
и мат.ожидания w0t .
x(t) =Е(t)cosy(t)=E(t)cos(w0t -j(t))=E(t)cosj(t)cosw0t+E(t)sinj(t)sinw0t
A(t) B(t)
A(t) и B(t) медленно меняющиеся функции . Получаются , как случайные
функции времени .
x(t)=A(t)cosw0t + B(t)sinw0t , где A(t) и B(t) - квадратурные составляющие
огибающей .
В этом колебание вектор Е(t) будет колебаться , т.е. показывать флуктуацию.
A(t)
E(t)
j(t)
B(t)
Свойства функций :
1. Энергетические спектры G (w) иG (w) одинаковые .
2. Законы распределения одинаковые w (x)=w (x)=wa(x)=wб(x).
3. Коррелляционные функции равны Bx(t )=B (t ) .
4. Справедливо свойство ортогональности .
ѕѕѕѕ ѕѕѕ
h(t)x(t)=0 A(t)B(t)=0
5.-Ґ <=A(t) < Ґ ; -Ґ <=B(t)<Ґ;E(t)>=0 .
ѕ ѕ
6. Если Гауссовский шум то A(t)=0 и B(t)=0
( Т.е. нулевые мат. ожидания ) .
Если A(t)=F то это значит что в случайном процессе
появилась детерменированная ф-ия .
x(t)=A(t)cosw0t + B(t)sinw0t+ Fcosw0t
 | |||||
 | |||||
 | |||||
7. A (t)=B (t) =Gx - мощность реализации .
ѕ ѕ ѕ
E (t)= A (t)+B (t) =2Gx - мощность огибающей .
Похожие работы
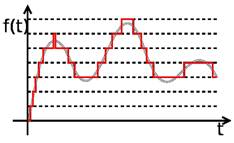
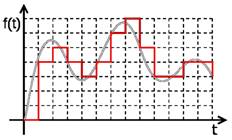
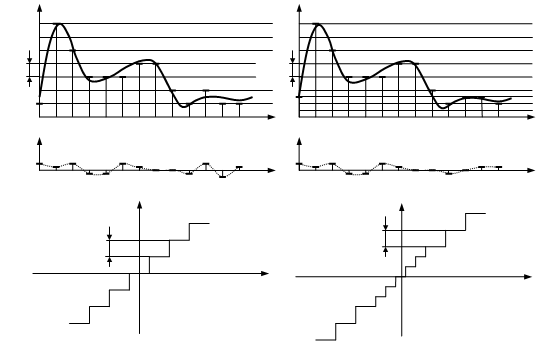
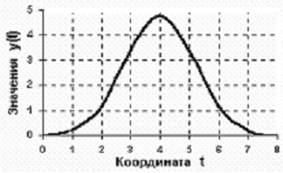
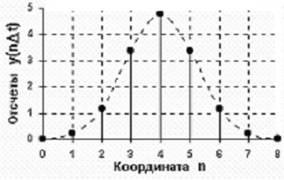
... сигнала уровень квантования называют также глубиной дискретизации или битностью. Глубина дискретизации измеряется в битах и обозначает количество бит, выражающих амплитуду сигнала. Чем больше глубина дискретизации, тем точнее цифровой сигнал соответствует аналоговому. В случае однородного квантования глубину дискретизации называют также динамическим диапазоном и измеряют в децибелах (1 бит ≈ ...
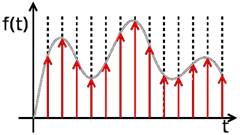
... иметь дело с данными, имеющими конечный размер, – например, с массивами чисел конечного размера и ограниченной разрядности. Рассмотренная выше теорема дискретизации дает такую возможность. Количество информации, энтропия источника сообщений Для сравнения между собой различных источников сообщений необходимо ввести некоторую количественную меру, которая дала бы возможность объективно ...
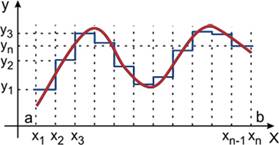
... функций в виде зависимости их значений от определенных аргументов Δвремени, линейной или пространственной координаты и т.п.) при анализе и обработке данных широко используется математическое описание сигналов по аргументам, обратным аргументам динамического представления. Так, например, для времени обратным аргументом является частота. Возможность такого описания определяется тем, что любой ...
... рисунков в формате А0-А1 со скоростью 10-30 мм/с. Фотонаборный аппарат Фотонаборный аппарат можно увидеть только в солидной полиграфической фирме. Он отличается своим высоким разрешением. Для обработки информации фотонаборный аппарат оборудуется процессором растрового изображения RIP, который функционирует как интерпретатор PostScript в растровое изображение. В отличие от лазерного принтера в ...
0 комментариев