Навигация
РАСЧЕТ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ МОЩНОСТИ
2. РАСЧЕТ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ МОЩНОСТИ
При заданной
автокорреляционной
функции ![]() , B(0)=1 B2 ,
, B(0)=1 B2 ,
p/p=0.1, =105 Гц требуется:
определить спектральную плотность мощности;
вычислить интервал корреляции ![]() и ширину спектральной плотность
и ширину спектральной плотность
мощности
![]() ;
;
найти и пояснить связь между ![]()
![]() и
и ![]() ;
;
построить графики функции ![]() и G(f);
и G(f);
определить верхнюю граничную частоту Fв случайного процесса;
Спектральная
плотность
мощности G(f)
центрированного
стационарного
процесса является
прямым преобразованием
Фурье от автокорреляционной
функции ![]() .
.
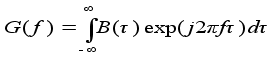 (1)
(1)
Разложив функцию exp получим:
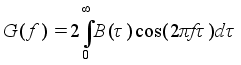 (2)
(2)
Подставим выражение для автокорреляционной функции :
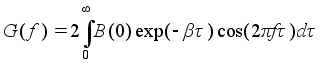
При вычислении G(f) воспользуемся табличным интегралом:
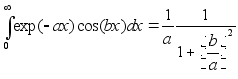 (3)
(3)
получим окончательную формулу:
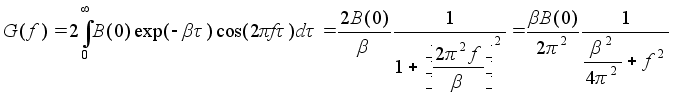
Подставив начальные условия получим выражение для спектральной плотности мощности:
![]()
Рассчитаем
интервал корреляции
![]() по
методу эквивалентного
прямоугольника:
по
методу эквивалентного
прямоугольника:
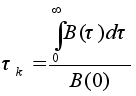 (4)
(4)
так как
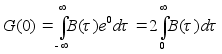 и
и ![]() получим:
получим:
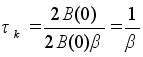 (5)
(5)
Подставив значение получим:
![]() c=10мкс
c=10мкс
Ширину
спектральной
плотности
мощности ![]() также определим
по методу
эквивалентного
прямоугольника:
также определим
по методу
эквивалентного
прямоугольника:
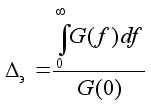 (6)
(6)
Используя обратное преобразование Фурье получим;
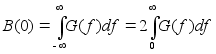 (7)
(7)
Формула (6) примет вид:
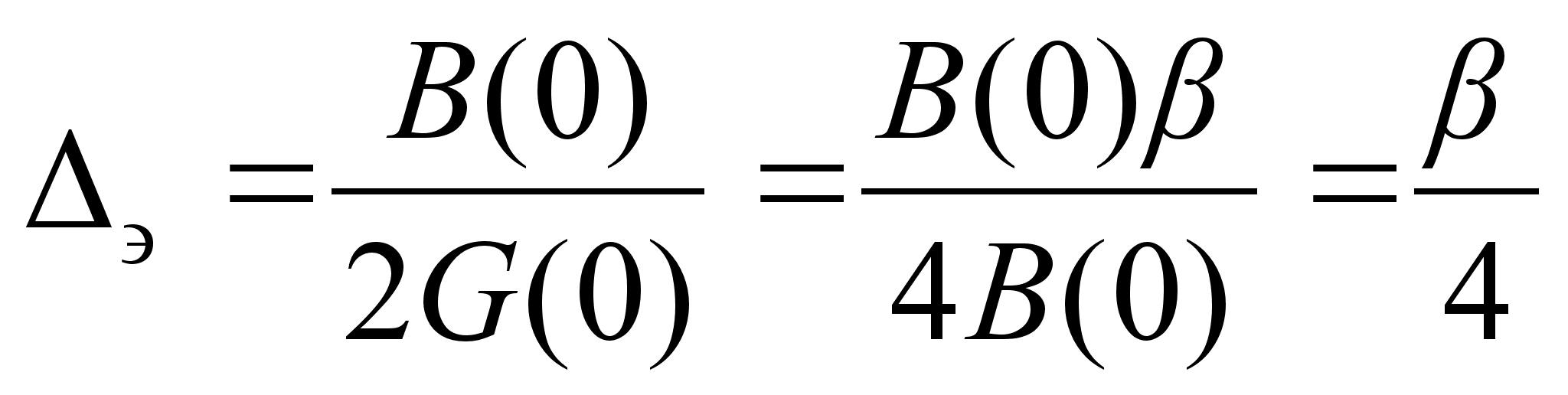
Подставив значение получим:
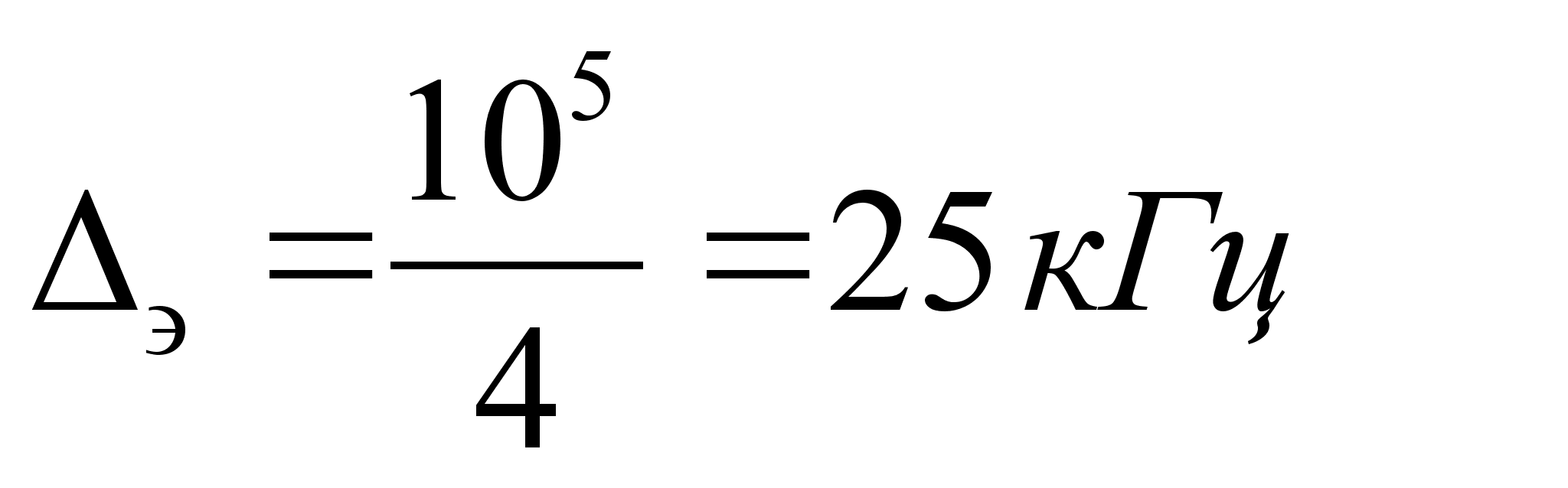
Связь между ![]() и
и ![]() найдем перемножив
их.
найдем перемножив
их.
![]() (8)
(8)
Таким образом произведение
![]() равно постоянной
величине, то
есть между
равно постоянной
величине, то
есть между ![]() к
и
к
и ![]() э
существует обратная зависимость.
При увеличении
времени корреляции
происходит
уменьшение
ширины спектральной
плотности
мощности.
Следовательно,
медленно протекающий
случайный
процесс, имеющий
большое время
корреляции,
будет иметь
относительно
узкую ширину
спектральной
плотности, а
быстродействующий процесс будет иметь малое
время корреляции
и относительно
большое значение
ширины спектральной
плотности
мощности.
э
существует обратная зависимость.
При увеличении
времени корреляции
происходит
уменьшение
ширины спектральной
плотности
мощности.
Следовательно,
медленно протекающий
случайный
процесс, имеющий
большое время
корреляции,
будет иметь
относительно
узкую ширину
спектральной
плотности, а
быстродействующий процесс будет иметь малое
время корреляции
и относительно
большое значение
ширины спектральной
плотности
мощности.
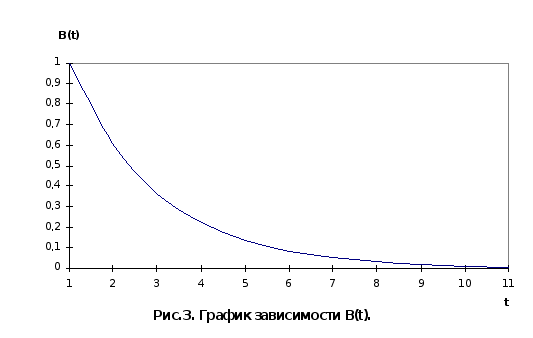
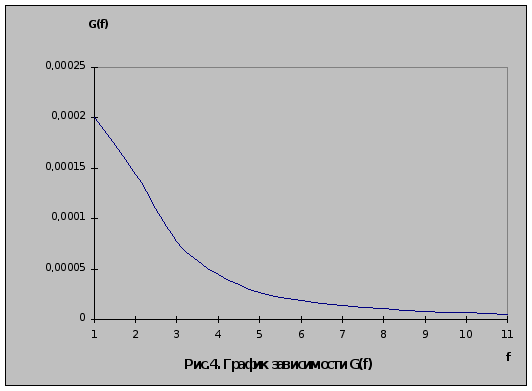
Используя
графический
редактор Еxell
построим графики
зависимостей
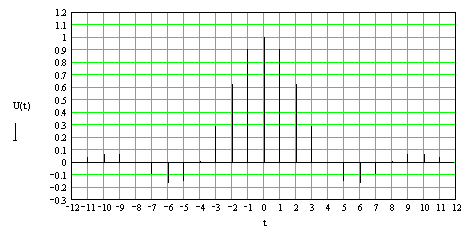
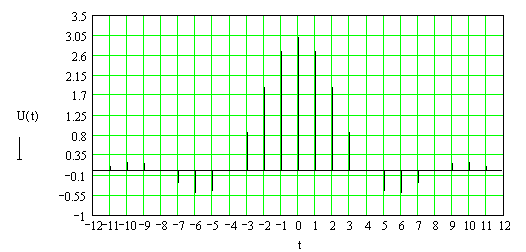
![]() и G(f). Они изображены
на рис.3. и рис.4.
и G(f). Они изображены
на рис.3. и рис.4.
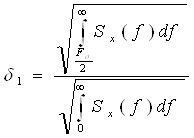
Определим
верхнюю граничную
частоту Fв,
используя
выражение:![]()
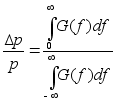 (9)
(9)
применив обратное преобразование Фурье (7) и табличный интеграл
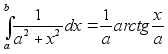 (10)
(10)
подставив значение G(f) получим:
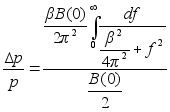
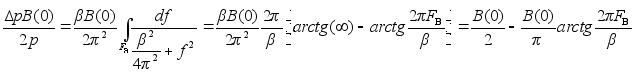
![]()
Возьмем тангенс с правой и левой стороны
![]()
![]()
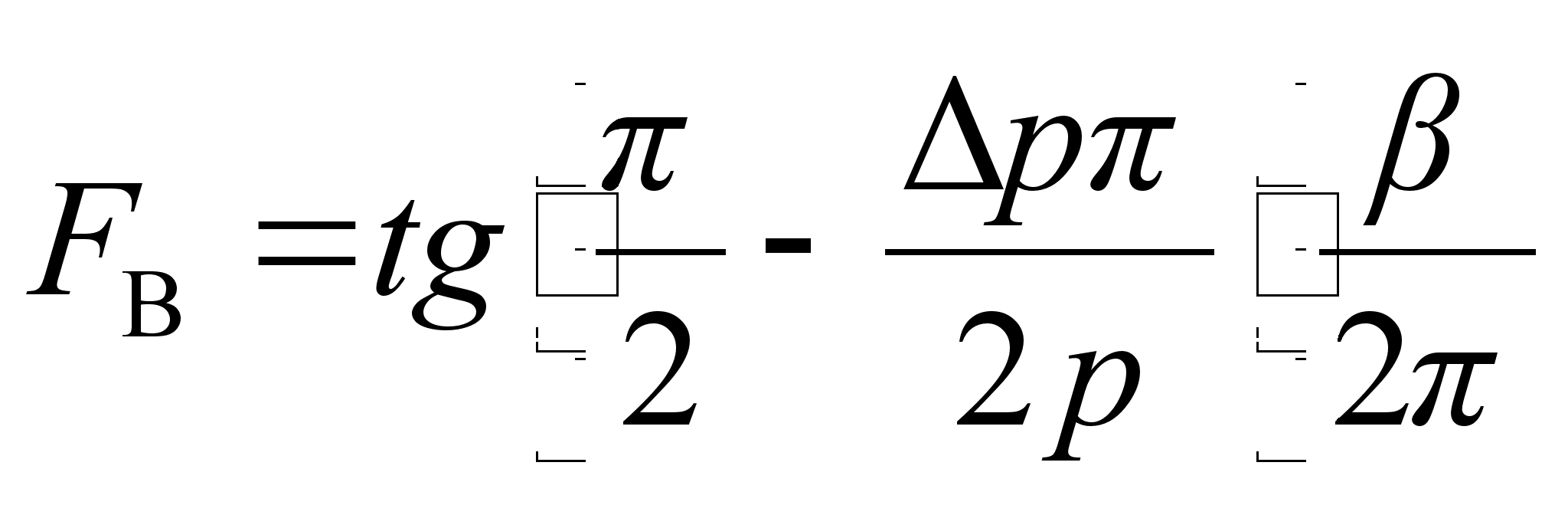 (11)
(11)
Подставив значения получим:
![]()
Похожие работы
... дискретным каналом. При этом необходимо преобразовать непрерывное сообщение в цифровой сигнал, т.е. в последовательность символов, сохранив содержащуюся в сообщении существенную часть информации. Типичными примерами цифровых систем передачи непрерывных сообщений являются системы с импульсно–кодовой модуляцией (ИКМ) и дельта–модуляцией (ДМ). Для преобразования непрерывного сообщения в цифровую ...
... несущими и амплитудно-фазовая модуляция с одной боковой полосой (АФМ-ОБП). 3. Выбор длительности и количества элементарных сигналов, используемых для формирования выходного сигнала В реальных каналах связи для передачи сигналов по частотно ограниченному каналу используется сигнал вида , но он бесконечен во времени, поэтому его сглаживают по косинусоидальному закону. , где - ...
... Вид сигнала при модуляции прямоугольными импульсами со скважностью 2: рис. 3 Для отыскания спектра сигнала ДФМ запишем: Спектры сигналов для различных значений: Рис. 4 2.3 Расчет вероятности ошибки на выходе приемника. Вероятность ошибки на выходе приемника определяется формулой где Ф() – функция Крампа q – отношение мощности сигнала к ...
стемы. Содержание Нормативные ссылки Введение 1 Расчет информационных характеристик источников дискретных сообщений 2 Расчет информационных характеристик дискретного канала 3 Согласование дискретного источника с дискретным каналом 4 Дискретизация и квантование Заключение Нормативные ссылки В настоящем отчете использованы ссылки на следующие стандарты: - ГОСТ 1.5 – 93 ...
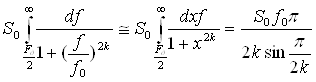

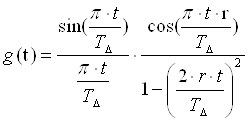
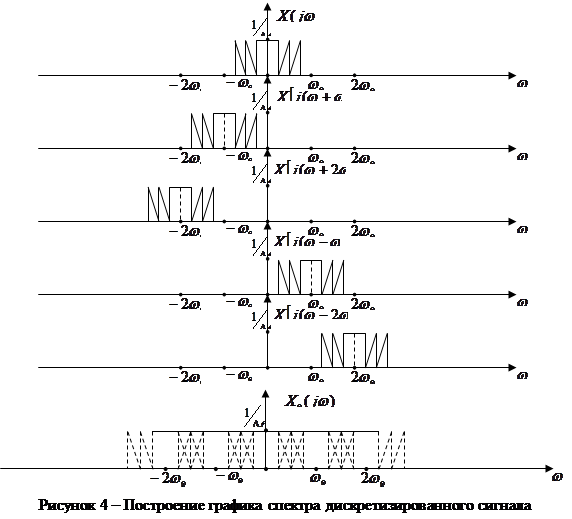
0 комментариев