Навигация
СТРУКТУРНАЯ СХЕМА И АЛГОРИТМ РАБОТЫ ОПТИМАЛЬНОГО ПРИЕМНИКА
7. СТРУКТУРНАЯ СХЕМА И АЛГОРИТМ РАБОТЫ ОПТИМАЛЬНОГО ПРИЕМНИКА.
Для некогерентного приема и ЧМ манипуляции требуется :
нарисовать структурную схему оптимального приемника и записать
алгоритм работы;
вычислить вероятность неправильного приема декретного двоичного
сигнала при отношении энергии сигнала к спектральной плотности
шума на выходе детектора h2=169;
построить графики зависимости Pош=f(h) для ЧМ и ФМ и сравнить их.
Целью оптимального приема повышение верности принимаемого сообщения, эта задача решается выбором оптимальной структуры приемника.
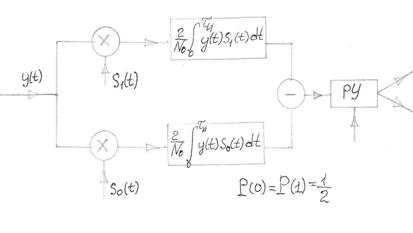
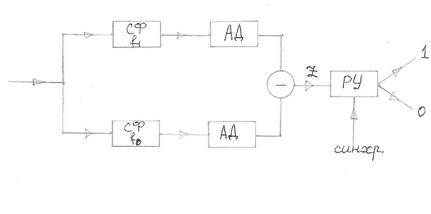
Задача приемника заключается в следующем: он анализирует смесь сигнала и шума Z(t) в течение единичного интервала времени и на основании этого анализа принимает решение, какой из возможных сигналов присутствует на входе приемника. Структурная схема оптимального демодулятора, построенного на согласованных фильтрах для приёма ЧМ сигнала приведена на рис.6.
![]()
Е1/No




![]()
![]()
![]()
![]()
![]() СФ1 АД1 СУ1
СФ1 АД1 СУ1
![]()
![]() Z(t) РУ bi*
Z(t) РУ bi*



![]()
![]()
![]()
![]() СФ2 АД2 СУ2
СФ2 АД2 СУ2
![]()
Е2/No
Рис.6
Смесь сигнала и шума Z(t) фильтруется согласованным фильтром, а затем выделяется огибающая сигнала на выходе этого фильтра. Огибающая сравнивается с пороговым уровнем, величина которого при равных априорных вероятностях P(U1(t)=P(U2(t) определяется соотношением Ei/No. Если эти вероятности не равны, пороговый уровень изменится на lnP(U1(t)/P(U2(t). При превышении порогового уровня в верхнем канале принимается решение bi*=1, а если в нижнем, то bi*=0. Временные диаграммы поясняющие работу оптимального демодулятора ЧМ сигнала приведены на рис.7
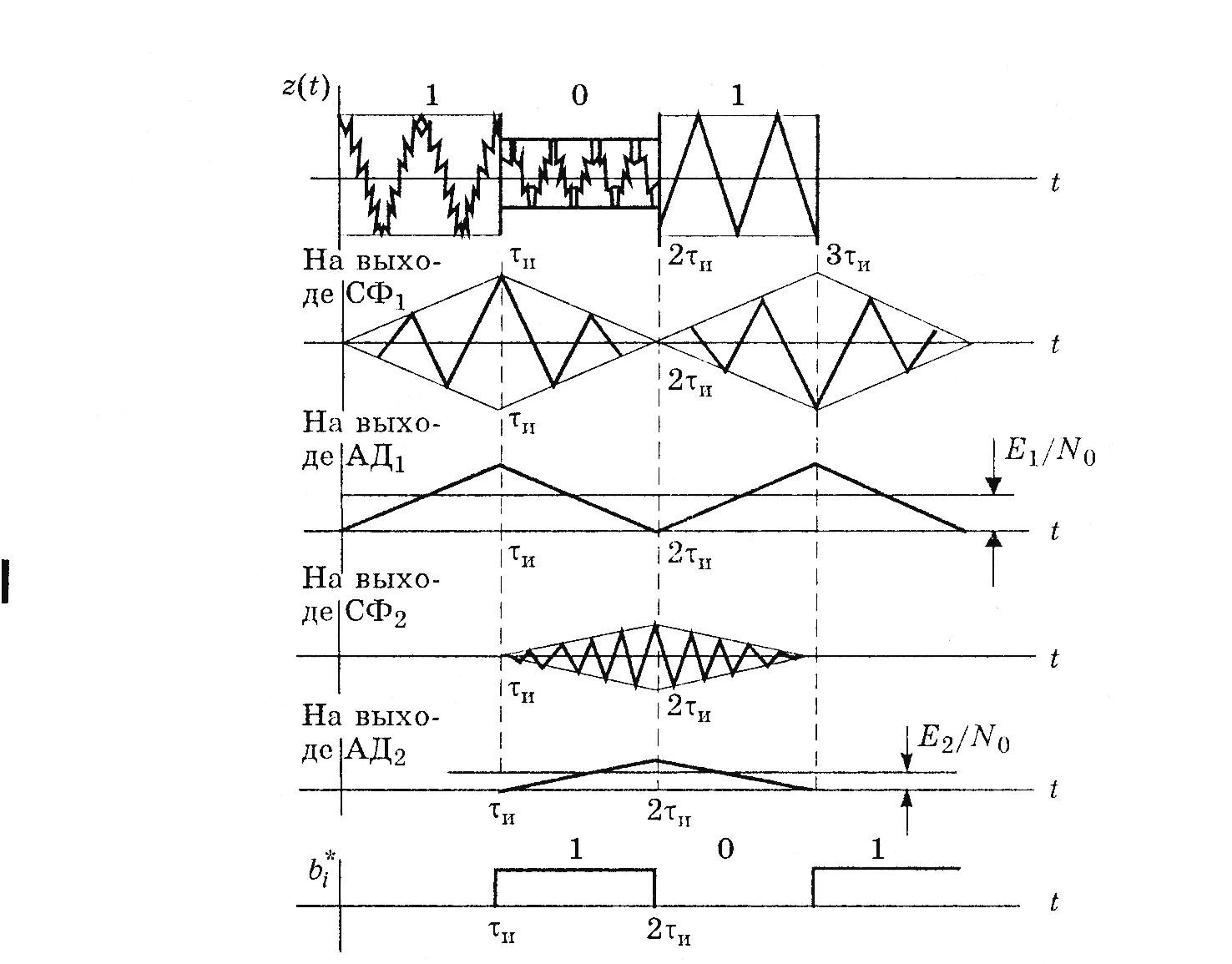
Рис. 7.
Алгоритм приёма имеет вид:
Т Т Z(t)Si(t)dt – 0.5Ei > Z(t)Sj(t)dt – 0.5Ej; ji,
0
где Ej – энергия ожидаемого сигнала.
Устройство, непосредственно вычисляющее скалярное произведе- ние: Т
(Z,Si) – Z(t)Si(t)dt , называют активным фильтром, или коррелятором.
0
Поэтому приёмник реализующий данный алгоритм называют корреляционным.
Вероятность неправильного приёма дискретного двоичного сигнала для ЧМ модуляции, при отношении энергии сигнала к спектральной плотности шума на выходе детектора h2=169, определим по формуле:
P=0,5 e –0.5 h2=0,5 e - 84,5 = 10-37
Вероятность ошибки для ЧМ сигнала определяется по формуле:
Pош=0,5[1-Ф(h)],
где 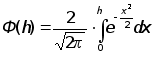 - функция
Крампа.
- функция
Крампа.
Для когерентного приёма фазомодулированного сигнала вероятность ошибки определяется по формуле:
Pош=0.5[1-Ф(![]() h)]
h)]
Все рассчитанные данные занесём в таблицу 1.
Графики зависимости Pош=f(h), для приёма ЧМ и ФМ сигналов, построенные с помощью программы Exell, приведены на рис.8.
Таблица 1
| ЧМ | ФМ | ||||
| h | Ф(h) | Pчм | 2 h | Ф(2 h) | Pфм |
| 0 | 0 | 0,5 | 0 | 0 | 0,5 |
| 0,2 | 0,1585 | 0,421 | 0,2828 | 0,2205 | 0,3898 |
| 0,4 | 0,3108 | 0,344 | 0,5657 | 0,4313 | 0,2844 |
| 0,6 | 0,4515 | 0,274 | 0,8485 | 0,6047 | 0,1977 |
| 0,8 | 0,5763 | 0,211 | 1,1314 | 0,7415 | 0,1293 |
| 1,0 | 0,6827 | 0,158 | 1,1442 | 0,8415 | 0,0793 |
| 1,2 | 0,7699 | 0,115 | 1,6971 | 0,9109 | 0,0446 |
| 1,4 | 0,8385 | 0,081 | 1,9799 | 0,9523 | 0,0239 |
| 1,6 | 0,8904 | 0,053 | 2,2627 | 0,9756 | 0,0122 |
| 1,8 | 0,9281 | 0,035 | 2,5456 | 0,9892 | 0,0054 |
| 2,0 | 0,9544 | 0,021 | 2,8284 | 0,9956 | 0,0022 |
| 2,2 | 0,9722 | 0,0139 | 3,113 | 0,99806 | 0,000097 |
| 2,4 | 0,9836 | 0,0082 | 3,3941 | 0,99933 | 0,000033 |
| 2,6 | 0,9907 | 0,00465 | 3,6770 | 0,99978 | 0,000011 |
| 2,8 | 0,9949 | 0,00255 | 3,9598 | 0,99994 | 0,000003 |
| 3,0 | 0,9973 | 0,00135 | 4,2408 | 0,99997 | 0,000001 |
| 3,2 | 0,9986 | 0,00068 | 4,5255 | 0,99998 | 0,0000005 |
| 3,4 | 0,9993 | 0,00035 | 4,8083 | 0,99999 | 0,0000001 |
| 3,6 | 0,99968 | 0,00016 | |||
| 3,8 | 0,99986 | 0,00007 | |||
| 4,0 | 0,99994 | 0,00003 | |||
| 4,2 | 0,99997 | 0,00001 | |||
| 4,4 | 0,99999 | 0,000005 | |||
Сравнивая полученные результаты зависимостей Pош(h) для ЧМ и ФМ мы видим ,что фазовая модуляция является более помехоустойчивой, чем частотная.
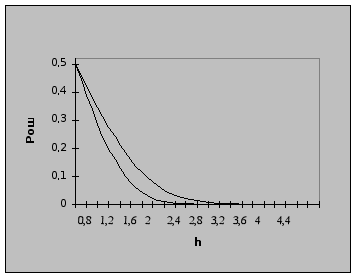
![]() Рчм
Рчм
Рфм
![]()
Рис.8
ЗАКЛЮЧЕНИЕ.
Фундаментальными работами В.А.Котельникова и К.Шенонна было положено начало современной теории передачи сообщений. Классическая теория помехоустойчивости при флуктуационных помехах развита для каналов со случайно изменяющимися параметрами и продолжает развиваться в направлении учета реальных характеристик сигналов и помех, в том числе нестационарных. Вопросы синтеза оптимальных приемников непрерывных и импульсных сигналов успешно решаются на основании теории нелинейной фильтрации. Дальнейшим шагом является разработка и применение методов построения оптимальных схем, позволяющих обеспечить высокую достоверность передачи сообщений в каналах с переменными параметрами при неполной априорной информации о сигналах и помехах.
Современная теория передачи сообщений позволяет достаточно полно оценить различные системы связи по их помехоустойчивости и эффективности и тем самым определить, какие из этих систем являются наиболее перспективными. Теория достаточно четко указывает не только возможности совершенствования существующих систем связи, но и пути создания новых, более совершенных систем.
В настоящее время речь идет о создании систем, в которых используются показатели эффективности, близкие к предельным. Одновременное требование высоких скоростей и верности передачи приводит к необходимости применения систем, в которых используются многопозиционные коды и мощные корректирующие коды.
В реальных условиях системы связи должны выполнять большой объем вычислений и логических операций, связанных с изменением и регулированием параметров сигнала, а также с операциями кодирования и декодирования. Наиболее совершенная система связи должна быть сложной саморегулирующейся системой. Практически реализация таких систем должна базироваться на использовании микропроцессоров и ЭВМ.
ЛИТЕРАТУРА.
1. Клюев Л.Л. “Теория электрической связи». Минск, «Дизайн ПРО»,
1998 г.
2. Шувалов Б.П., Захарченко Н.Б., Шварцман В.О. и др ”Передача дис-
кретных сообщений”: Под ред. Шувалова -М.; Радио и связь 1990
Похожие работы
... дискретным каналом. При этом необходимо преобразовать непрерывное сообщение в цифровой сигнал, т.е. в последовательность символов, сохранив содержащуюся в сообщении существенную часть информации. Типичными примерами цифровых систем передачи непрерывных сообщений являются системы с импульсно–кодовой модуляцией (ИКМ) и дельта–модуляцией (ДМ). Для преобразования непрерывного сообщения в цифровую ...
... несущими и амплитудно-фазовая модуляция с одной боковой полосой (АФМ-ОБП). 3. Выбор длительности и количества элементарных сигналов, используемых для формирования выходного сигнала В реальных каналах связи для передачи сигналов по частотно ограниченному каналу используется сигнал вида , но он бесконечен во времени, поэтому его сглаживают по косинусоидальному закону. , где - ...
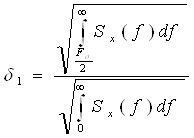
... Вид сигнала при модуляции прямоугольными импульсами со скважностью 2: рис. 3 Для отыскания спектра сигнала ДФМ запишем: Спектры сигналов для различных значений: Рис. 4 2.3 Расчет вероятности ошибки на выходе приемника. Вероятность ошибки на выходе приемника определяется формулой где Ф() – функция Крампа q – отношение мощности сигнала к ...
стемы. Содержание Нормативные ссылки Введение 1 Расчет информационных характеристик источников дискретных сообщений 2 Расчет информационных характеристик дискретного канала 3 Согласование дискретного источника с дискретным каналом 4 Дискретизация и квантование Заключение Нормативные ссылки В настоящем отчете использованы ссылки на следующие стандарты: - ГОСТ 1.5 – 93 ...

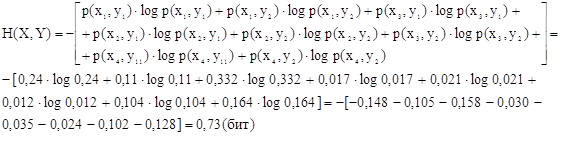
0 комментариев