Навигация
Мендель Виктор Васильевич, доцент кафедры геометрии ХГПУ
Цель предлагаемого задания – повторить материал по планиметрии для дальнейшего его использования при решении задач по стереометрии, а также применения при решении олимпиадных задач.
Предлагаемая разработка состоит из двух блоков. В первом изложены основные геометрические конструкции и связанные с ними факты; основные вычислительные формулы и замечательные теоремы, связанные с геометрией треугольника.
Во втором блоке собраны задачи. Начинается этот блок с опорных задач, которые нужно обязательно разобрать. Далее изложены задачи для самостоятельного решения. Они разделены по уровню сложности и по тематике. Некоторые снабжены указаниями к решению.
Вам необходимо внимательно прочитать и повторить материал первого блока. Решить опорные задачи (решения этих задач высылать не надо). Затем вы должны решить из задач для самостоятельного решения необходимый минимум (или больше). Минимальное количество задач по каждому разделу указано в начале каждого раздела. Если в школе учится несколько учащихся Заочной краевой физмат школы, им рекомендуется решать различные задачи.
Оформление решения:Номер задачи. Краткая запись (текст можно не переписывать). Пояснение всех обозначений (Например: АН – высота из вершины А; ВМ – медиана; l – длина биссектрисы CL и т.п.).
Аккуратный чертеж с четкими обозначениями.
Решение (с необходимыми короткими комментариями. Например: из того, что треугольник ABC – прямоугольный — следует … , из Δ ABC по теореме косинусов выразим сторону BC и т.п.). При оформлении решения допускаются ссылки на материал первого блока.
I. Основные геометрические конструкции, вычислительные формулы и теоремы.
Основные конструкции.
Треугольник с построенными медианами.
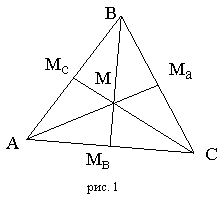 Медианы пересекаются в одной точке (центроид, центр тяжести) и делятся этой точкой в отношении 2:1 считая от вершины.
Медианы пересекаются в одной точке (центроид, центр тяжести) и делятся этой точкой в отношении 2:1 считая от вершины.
Медиана разбивает треугольник на два равных по площади треугольника.
Медианы разбивают треугольник на шесть равных по площади треугольников.
Площади треугольников АМВ, ВСМ и САМ – равны.
Если точка М лежит внутри треугольника и обладает свойством 4, то это точка пересечения медиан.
Треугольник с построенными высотами.
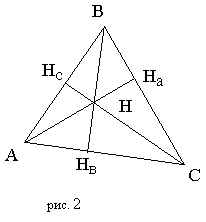 Прямые, содержащие высоты треугольника, пересекаются в одной точке (точка пересечения высот, ортоцентр).
Прямые, содержащие высоты треугольника, пересекаются в одной точке (точка пересечения высот, ортоцентр).
Если треугольник остроугольный – Н лежит внутри него, если тупоугольный – вне треугольника, если прямоугольный – совпадает с вершиной прямого угла.
Треугольник АВС и АНВНС – подобны: 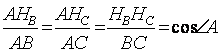 .
.
Четырехугольник ВСНВНС вписывается в окружность: ÐВСНВ+ÐНВНСВ=180°.
Четырехугольник АНСННВ вписывается в окружность: ÐА+ÐНСННВ=180°.
Середины сторон треугольника, основания его высот и середины отрезков, соединяющих ортоцентр с вершинами лежат на одной окружности (окружность девяти точек).
Треугольник с построенными биссектрисами.
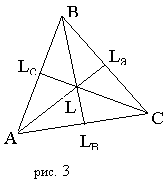 Основное свойство биссектрис:
Основное свойство биссектрис: 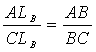 (то же верно и для биссектрисы внешнего угла треугольника).
(то же верно и для биссектрисы внешнего угла треугольника).
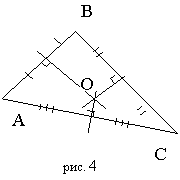
Биссектрисы пересекаются в одной точке L – центре вписаной окружности.
Расстояние от точки L до любой стороны треугольника равно r – радиусу вписанной окружности.
Замечание! Точки LA, LB и LC в общем случае не являются! точками касания сторон треугольника и вписанной окружности.
 Треугольник с построенными серединными перпендикулярами.
Треугольник с построенными серединными перпендикулярами.
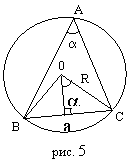
Серединные перпендикуляры пересекаются в одной точке О – центре описанной окружности. Точка О равноудалена от вершин: ОА=ОВ=ОС=R – радиус описанной окружности.
(см. рис. 5) ![]() . Теорема синусов:
. Теорема синусов: ![]() .
.
Точка О лежит:
внутри остроугольного треугольника;
 на середине гипотенузы прямоугольного треугольника;
на середине гипотенузы прямоугольного треугольника;
вне тупоугольного треугольника.
Связь между серединными перпендикулярами и высотами: высоты треугольника НАНВНС (см. рис.2) лежат на серединных перпендикулярах треугольника АВС.
Треугольник с построенными средними линиями.
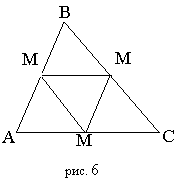 средняя линия – отрезок, соединяющий середины 2-х сторон треугольника. Средняя линия МАМВ параллельна стороне АВ и равна половине ее длины.
средняя линия – отрезок, соединяющий середины 2-х сторон треугольника. Средняя линия МАМВ параллельна стороне АВ и равна половине ее длины.
Средние линии образуют треугольник, подобный данному. Коэффициент подобия – 1/2, площади относятся как 1:4.
Про описанную окружность треугольника МАМВМС смотри 1.2 №6.
Про его высоты смотри 1.4 № 4.
Углы, вписанные в окружность.
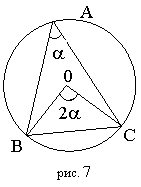 Угол, вершина которого лежит на данной окружности, а стороны ее пересекают, называется вписанным.
Угол, вершина которого лежит на данной окружности, а стороны ее пересекают, называется вписанным.
Градусная мера дуги ВС окружности есть градусная мера центрального угла ВОС, опирающегося на эту дугу.
Угол ВАС равен половине угла ВОС (мера вписанного угла равна половине меры дуги, на которую этот угол опирается).
Сумма противоположных углов вписанного 4-х угольника равна 180º.
Вписанные углы, опирающиеся на равные дуги равных окружностей (или одной окружности) – равны.
Будем говорить, что отрезок АВ виден из точки М под углом γ, если ÐАМВ=γ.
Если одна из сторон выпуклого многоугольника видна из всех оставшихся вершин под одним и тем же углом, то вокруг этого многоугольника можно описать окружность (обратное также верно).
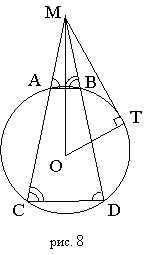 Угол, вершина которого лежит вне окружности, а стороны пересекают
Угол, вершина которого лежит вне окружности, а стороны пересекают
эту окружность.
ÐСМD=1/2×(ÐСОD-ÐAOB) – угол равен полуразности мер дуг, которые он вырезает из окружности.
Треугольники АМВ и СМD – подобны: ![]() ; ÐМАВ=ÐМDС, ÐМВА=ÐМСD.
; ÐМАВ=ÐМDС, ÐМВА=ÐМСD.
Свойство отрезков секущих: МА·МС=МВ·МD=МТ2=МО2-R2 (MT – отрезок касательной, МО – расстояние от М до центра О, R – радиус окружности).
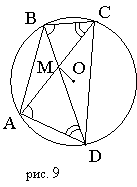 Угол, вершина которого лежит внутри окружности.
Угол, вершина которого лежит внутри окружности.
![]() – угол равен полусумме мер дуг, которые он вырезает из окружности.
– угол равен полусумме мер дуг, которые он вырезает из окружности.
Треугольники МВС и МАD подобны: ÐМВС=ÐМАD; ÐМСВ=ÐМDА (т.к. опираются на равные дуги). МА:МВ=МС:МD=ВС:АD.
Свойство отрезков секущих: МА·МС=МВ·МD= =R2-МО2.
Выпуклый многоугольник, описанный вокруг окружности.
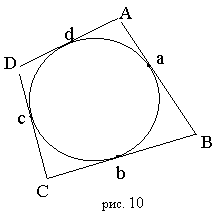 Многоугольник описан вокруг окружности, если все его стороны касаются этой окружности.
Многоугольник описан вокруг окружности, если все его стороны касаются этой окружности.
Центр вписанной окружности равноудален от сторон многоугольника. Если внутри выпуклого многоугольника есть точка, равноудаленная от всех его сторон, то в этот многоугольник вписывается окружность с центром в данной точке.
В выпуклый 4-х угольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны: a+c=b+d.
Радиус r вписаной окружности многоугольника вычисляется по формуле ![]() , где S – площадь, а P – периметр многоугольника.
, где S – площадь, а P – периметр многоугольника.
Теоремы Вариньона.
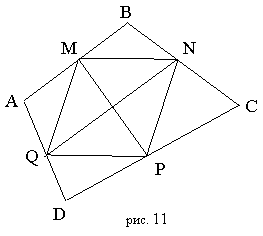 Середины сторон 4-х угольника являются вершинами параллелограмма (рис. 11).
Середины сторон 4-х угольника являются вершинами параллелограмма (рис. 11).
Отрезки, соединяющие середины противоположных сторон и середины диагоналей 4-х угольника пересекаются в одной точке и делятся этой точкой пополам.
Если 4-х угольник из п.2 – выпуклый, то площадь параллелограмма MNPQ равна половине площади ABCD.
Свойства хорд.
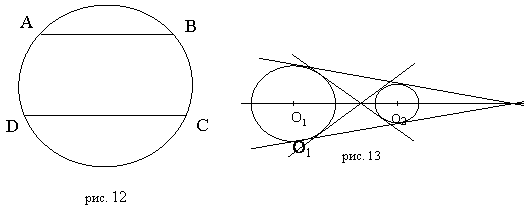 |
Прямая, проходящая через середины двух параллельных хорд окружности проходит через центр этой окружности.
Серединный перпендикуляр к хорде проходит через центр окружности.
Параллельные хорды AB и CD (рис. 12) высекают на окружности равные дуги AD и BC.
Равные хорды одной (или двух равных) окружности стягивают равные дуги.
Угол между хордой АВ и касательной в точке А равен половине меры дуги АВ.
Линия центров двух окружностей.
Линия центров – прямая, проходящая через центры двух окружностей.
Общие внешние (внутренние) касательные двух окружностей пересекаются в точках, лежащих на линии центров.
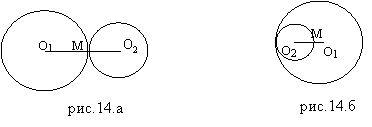 |
Если две окружности касаются, то точка касания лежит на линии центров.
Основные вычислительные формулы.
Теорема косинусов: ![]()
Площадь треугольника: ![]()
![]() – стороны треугольника,
– стороны треугольника, ![]() – углы,
– углы,![]() – высота,
– высота,![]() – полупериметр,
– полупериметр, ![]() – радиус описаной окружности,
– радиус описаной окружности, ![]() – радиус вписаной окружности.
– радиус вписаной окружности.
Площадь выпуклого четырехугольника: ![]() ,
, ![]() и
и ![]() – диагонали,
– диагонали, ![]() – угол между ними.
– угол между ними.
2.4. Площадь выпуклого многоугольника с периметром![]() , описанного вокруг окружности радиуса
, описанного вокруг окружности радиуса ![]() :
: ![]() .
.
2.5.Формула Герона для вычисления площади треугольника: ![]() , где
, где ![]() .
.
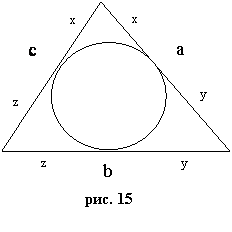 2.6.Длина отрезков, на которые делят стороны треугольника точки касания вписаной окружности:
2.6.Длина отрезков, на которые делят стороны треугольника точки касания вписаной окружности:![]() ,
, ![]() ,
, ![]()
2.7.Теорема Птолемея: во вписаном 4-х угольнике произведение диагоналей равно сумме произведений противоположных сторон: ![]() .
.
2.8.Площадь трапеции: ![]() ,
, ![]() и
и ![]() – основания,
– основания, ![]() – высота трапеции.
– высота трапеции.
2.9.Чтобы найти радиус окружности, описанной вокруг многоугольника, нужно найти радиус окружности, описанной вокруг треугольника, вершинами которого служат три каких-либо вершины данного многоугольника.
Похожие работы
... равенств (1) и (2) и сделав необходимые сокращения мы получим выражение (**). Обратное утверждение доказывается методом “ от противного“ также, как и в теореме Менелая. Некоторые рекомендации по применению теоремы Менелая для решения задач. Одним из замечательных свойств геометрических задач является многообразие методов их решения. Это часто заводит в тупик школьников и абитуриентов, которым ...
... о фигурах в одном трёхмерном евклидовом пространстве геометрия за 40 - 50 лет превратилась в совокупность разнообразных теорий, лишь в чём-то сходных со своей прародительницей - геометрией Евклида. Аксиомы планиметрии Аксиомы принадлежности - Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. - Через любые две точки можно провести ...
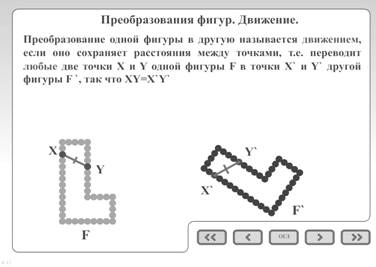
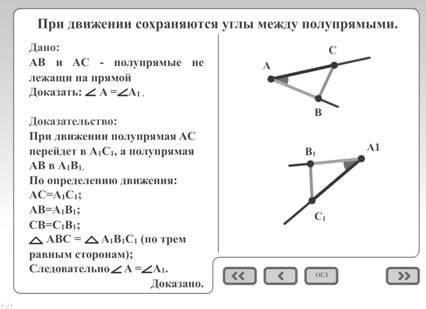
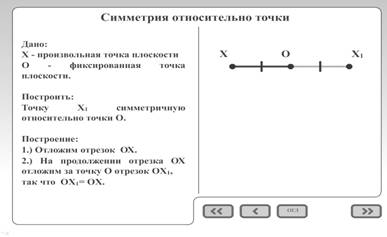
... Остальные понятия, такие как сонаправленность полупрямых и равенство фигур, рекомендуется изучать классическим способом. Т.к. благодаря мультимедийному пособию ученикам уже известны основные свойства движений и они с помощью учителя без особых усилий смогут применить накопленные знания при изучении данных тем. Например, в теме «сонаправленность полупрямых» основным элементом является параллельный ...
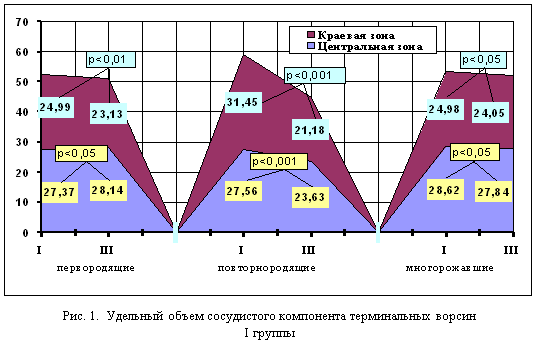
... мало сведений по морфометрии и в особенности сосудистых компонентов хориальных ворсин плаценты женщин, проживающих в сурьмяной биогеохимической провинции (СБГХП). С учетом вышесказанного, целью данной работы явилось изучение планиметрических особенностей структурных компонентов сосудистого хориона жительниц проживающих в СБГХП. Материал и методы исследования. Объектом исследования явились 142 ...


0 комментариев