Навигация
Проанализируем каждое ограничение двойственной задачи, подставляя вместо Y значения двойственных оценок
6. Проанализируем каждое ограничение двойственной задачи, подставляя вместо Y значения двойственных оценок
78*0.000247 +4*0.004369+1*0.473236 =0.5099 <=0.51
356*0.000247+2*0.004369+1*0.473236 =0.5699 <=0.57
14*0.000247 +5*0.004369+1*0.104691 =0.12999<=0.13
116*0.000247+45*0.004369+1*0.104691 =0.3299 <=0.33
65*0.000247 +15*0.004369+1*0.104691 =0.18628<=0.38
19*0.000247 +15*0.004369+1*0.64976 =0.71998<=0.72
12*0.000247 +1*0.217775 =0.2207 <=0.23
9*0.000247 +1*0.217775 =0.21999<=0.22
112*0.000247+1*0.473236 =0.5009 <=0.67
Из полученных данных видно, что все ресурсы используются оптимально, кроме сена суданки и комбикорма, которые вообще не вошли в рацион.
7. Для проведения анализа устойчивости оптимального плана прямой задачи при изменении коэффициентов целевой функции воспользуемся следующими данными, полученными с помощью ПЭВМ. Для этого в ответ на запрос RANGE вводим YES. Результы получим в следующем виде:
RANGES IN WHICH THE BASIS IS UNCHANGED:
OBJ COEFFICIENT RANGES
| VARIABLE | CURRENT | ALLOWABLE | ALLOWABLE |
| COEF | INCREASE | DECREASE | |
| x1 | 0.51 | 0.07 | 0.381798 |
| x2 | 0.57 | 0.485098 | 0.07 |
| x3 | 0.13 | 0.177986 | 0.093040 |
| x4 | 0.33 | 0.761069 | 0.177986 |
| x5 | 0.38 | INFINITY | 0.193695 |
| x6 | 0.72 | INFINITY | 0.649760 |
| x7 | 0.23 | INFINITY | 0.009258 |
| x8 | 0.22 | 0.009258 | 0.217775 |
| x9 | 0.67 | INFINITY | 0.169071 |
Как видно коэффициенты Cj при Xj в целевой функции могут изменяться таким образом:
0,128202 < C1 < 0,58
0,5 < C2 < 1,055098
0,03696 < C3 < 0,307986
0,152014 < C4 < 1,091069
0,186305 < C5 < INFINITY
0,07024 < C6 < INFINITY
0,220742 < C7 < INFINITY
0,002225 < C8 < 0,229258
0,500929 < C9 < INFINITY
Если коэффициенты целевой функции лежат соответственно в заданных диапазонах, то оптимальный план прямой задачи остается без изменений.
Соответственно оптимальный план двойственной задачи будет устойчив при изменении правых частей ограничений, заложенных в следующей таблице.
| ROW | CURRENT | ALLOWABLE | ALLOWABLE |
| RHS | INCREASE | DECREASE | |
| 2 | 15.3 | 5.870109 | INFINITY |
| 3 | 1758 | 1116.54 | 298.960100 |
| 4 | 118 | 52.828530 | INFINITY |
| 5 | 45.8 | 139.823500 | INFINITY |
| 6 | 660.8 | 117.2392 | 43.69926 |
| 7 | 18.8 | 7.903641 | INFINITY |
| 8 | 5 | 4.409440 | 3.181932 |
| 9 | 20 | INFINITY | 15 |
| 10 | 15 | 8.567274 | 9.957481 |
| 11 | 35 | INFINITY | 20 |
| 12 | 35 | 2.886976 | 15.53039 |
| 13 | 60 | INFINITY | 25 |
| 14 | 10 | 10 | 10 |
| 15 | 20 | INFINITY | 10 |
На основе проведенной лабораторной работы можно сделать следующий вывод: полученное решение прямой задачи является оптимальным, то есть ферма, используя данный рацион минимизирует его себестоимость, при этом питательная ценность рациона находится в пределах норм.
Список литературы1. А.Ф. Гамецкий, Д.И. Соломон Лабораторный практикум по курсу "Исследование операций" (для экономических специальностей), Кишинев, 1995.
2. Конспект лекций по предмету «Исследование операций» доктора экономики В. П. Зубрицкого
Похожие работы
... , не только поэтому: решение многих задач базируется на нем. Формулы Беллмана для динамического программирования ГЛАВА 3. ПРАКТИЧЕСКОЕ ОБОСНОВАНИЕ ТЕОРИИ Линейное программирование с использованием пакета прикладных программ Math Cad. Нахождение оптимального плана производства в первый год осуществляется с помощью прикладной программы Math Cad. Во второй год:
... организаций. Этот процесс включает комплекс инженерно-технических и экономических задач, решение которых должно обеспечить выбор наилучших путей совершенствования производства, развитие экономики предприятия, повышение благосостояния коллектива, улучшение экологии и других социальных условий. В основе разрабатываемых мероприятий находятся ориентиры в виде приростов показателей производственного и ...
... ,9 тыс. грн. Найдём производную от валовых издержек, тогда имеем: ВИ’ (Vпр)=ПрИ(Vпр) =0,1119*(Vпр) – 5,6098*(Vпр) + 91,676, грн / ед. 2.3 Определение оптимального объёма производства Определим оптимальный объём производства: 1) аналитическими методами: Ⅰ Сравнение валовых издержек с валовым доходом. Из метода сравнения валовых издержек с валовым доходом имеем что, оптимальный ...
... Ю.Н. Математические методы в экономике: Учебник.2-е изд. – М.: МГУ им. М.В. Ломоносова, Издательство «Дело и Сервис», 1999. – 368 с. 7. Монахов А.В. Математические методы анализа экономики. – Спб: Питер, 2002. – 176 с. 8. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов /В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др., Под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999. ...


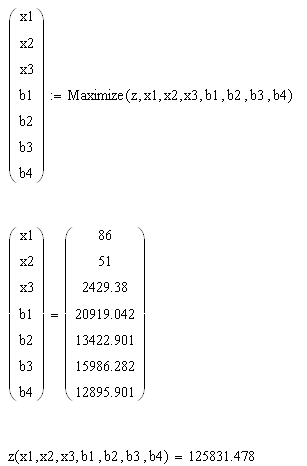

0 комментариев