Навигация
Метод субоптимизации на многообразиях. Задача квадратичного программирования
3.5 Метод субоптимизации на многообразиях. Задача квадратичного программирования.
Рассмотрим применение метода субоптимизации, рассмотренного в (3.4) к задаче квадратичного программирования (3.1.2). Как было ранее отмечено, условием успешного применения метода субоптимизации на многообразиях в задаче выпуклого программирования является существенная простота решения задачи (3.4.2) по сравнению с исходной задачей (3.4.1).
Рассмотрим эквивалентную (3.1.2) задачу:
|
|
(3.5.1) |
Запишем условия Куна-Таккера для задачи (3.5.1) с произвольным набором индексов Á :
|
|
(3.5.2) |
Используя ранее введенные обозначения (3.2.3-3.2.4), систему условий Куна-Таккера (3.5.2) можно записать следующим образом:
|
|
(3.5.3) |
Если множество UÁ порождает базис, вследствие (3.5.3) поиск минимума на многообразии XÁ представляет собой разложение вектора P0 по этому базису, т.е. эквивалентен решению системы линейных уравнений. Таким образом, метод субоптимизации на многообразиях в случае задачи квадратичного программирования оказывается эффективным в том случае, если в цепочке итерационного процесса встречаются только множества индексов, порождающие базисы.
Процедура метода строится на двух основных операциях, аналогичных блокам общего алгоритма субоптимизации на многообразиях для задачи выпуклого программирования.
Операция А. Пусть для некоторого набора индексов Á 0 определена оптимальная точка x* и множители Лагранжа l *k и D *j удовлетворяющие условиям Куна-Таккера совместно с оптимальным вектором x. Рассмотрим вспомогательное многообразие
|
| (3.5.4) |
Операция А состоит в нахождении оптимального вектора x*(q ), а также множителей Лагранжа, удовлетворяющих условиям Куна-Таккера задачи минимизации квадратичного функционала на многообразии (3.5.4).
Запишем условия Куна-Таккера для этой вспомогательной задачи:
|
|
Если набор индексов Á 0 порождает базис, то существует разложение вектора Pm+j0 по этому базису, имеющее следующий вид:
|
| (3.5.6) |
Подставляя это разложение в (3.5.5), и учитывая оптимальность набора x*,l *,D *, получаем следующие выражения для компонент оптимальной точки на многообразии (3.5.4):
|
|
(3.5.7) |
Таким образом, в случае, если набор индексов Á 0 порождает базис, операция А осуществляется тривиально, и определяется выражениями (3.5.7).
Суть операции А состоит в нахождении оптимальной точки на новом многообразии (3.5.4) по известной оптимальной точке на многообразии (3.4.4).
Операция Б. Пусть некоторое вспомогательное многообразие XÁ 0(q 1) таково, что одна из базисных компонент вектора x обратилась в ноль:
|
| (3.5.8) |
Суть операции Б состоит в переходе от многообразия XÁ 0(q 1) к другому многообразию XÁ 1 , соответствующему набору индексов Á 1 , определяемому следующим образом:
|
| (3.5.9) |
т.е. индекс j0 из (3.5.4) заменяется на индекс r из (3.5.8).
Учитывая (3.5.8), разложение (3.5.5) на многообразии XÁ 0 можно представить следующим образом:
|
| (3.5.10) |
Аналогично случаю, рассмотренному в операции А, что, если имеет место разложение:
|
| (3.5.11) |
причем выполнено соотношение
|
| (3.5.12) |
то условиям Куна-Таккера для задачи (3.5.1) соответствующей набору индексов Á 1 , удовлетворяют переменные, получаемые с помощью следующих формул:
|
|
(3.5.13) |
где
|
| (3.5.14) |
Учитывая вышеописанные условия, операция Б оказывается осуществимой в том случае, когда наборам индексов Á 0 и Á 1 соответствует базис UÁ 1,Á 0 . Операция Б является аналогом блока 4 общей схемы метода субоптимизации на многообразиях для задачи выпуклого программирования.
Для большей наглядности можно определить множество LÁ 1,Á 0 представляющее собой прямую, порождаемую базисом UÁ 1,Á 0 следующего вида:
|
| (3.5.15) |
Здесь ![]() - коэффициенты разложения вектора P0, а xir - вектора Pm+n+r по базису UÁ 1,Á 0. Заметим, что LÁ 1,Á 0(0) есть оптимальный вектор многообразия (3.5.4) при q =
- коэффициенты разложения вектора P0, а xir - вектора Pm+n+r по базису UÁ 1,Á 0. Заметим, что LÁ 1,Á 0(0) есть оптимальный вектор многообразия (3.5.4) при q = ![]() . Переход от этой точки к новому многообразию с помощью операции Б представляет собой движение по указанной прямой от дельта равного нулю в положительную (как будет показано позже) сторону.
. Переход от этой точки к новому многообразию с помощью операции Б представляет собой движение по указанной прямой от дельта равного нулю в положительную (как будет показано позже) сторону.
Похожие работы
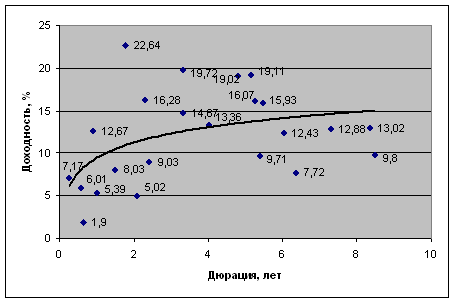
... негативных последствий для инвестиционного портфеля ОАО «МХК «ЕвроХим» и поиску путей формирования оптимальной структуры портфеля ценных бумаг организации на текущую дату. Рис. 4. Доходность еврооблигаций ОАО «МХК «ЕвроХим» на 02.03.2009 г. 3. Управление инвестиционным портфелем предприятия 3.1 Направления совершенствования структуры инвестиционного портфеля По сравнению с ...
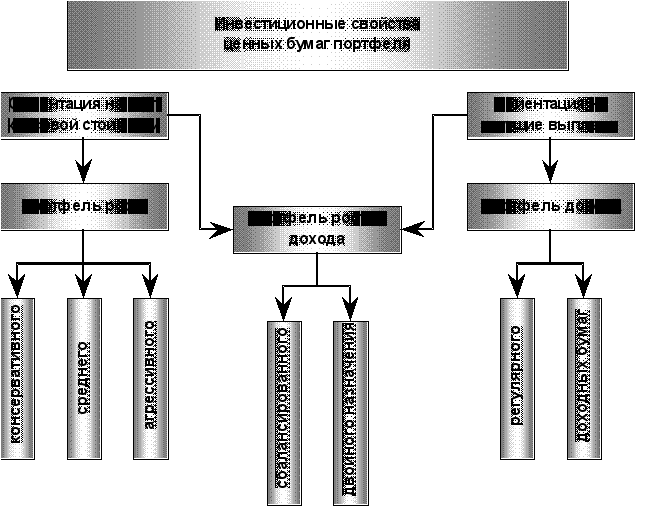
... реализацию следующих этапов: Постановка целей и выбор адекватного типа портфеля. Анализ объектов инвестирования. Формирование инвестиционного портфеля. Выбор и реализация стратегии управления портфелем. Оценка эффективности принятых решений. Первый этап включает определение целей инвестирования, способных обеспечить их достижение портфелей и необходимого объема вкладываемых средств. Следует ...
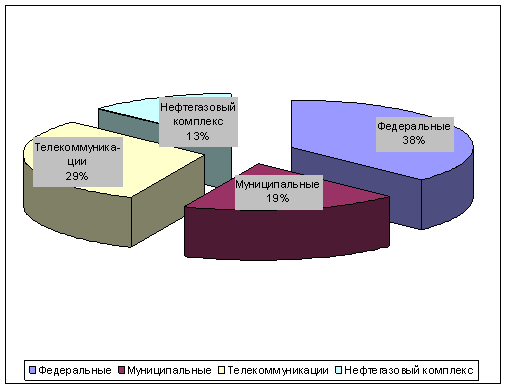
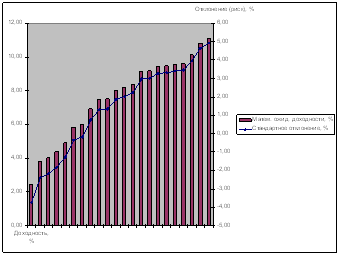
... МТС-ао 271,43 276,85 234,35 161,82 Сбербанк 72,65 65,31 44,72 31,13 Уркалий-ао 328 249,08 165,88 122,01 ГМКНорНик 5 050,91 4 917 3 379,26 1 850,28 2. Формирование инвестиционного портфеля При формировании портфеля ценных бумаг учитывается уровень ожидаемой доходности и уровень риска той или иной ценной бумаги. При расчете текущей доходности мы используем следующую формулу: ...
... , портфель ценных бумаг является тем инструментом, с помощью которого инвестору обеспечивается требуемая устойчивость дохода при минимальном риске. 3. ПРИНЦИПЫ ФОРМИРОВАНИЯ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ При формировании инвестиционного портфеля следует руководствоваться следующими соображениями: безопасность вложений (неуязвимость инвестиций от потрясений на рынке инвестиционного капитала), ...
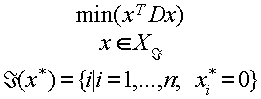
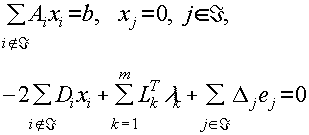
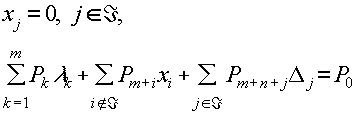
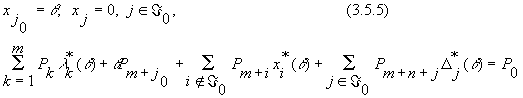
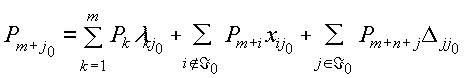
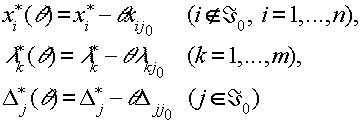
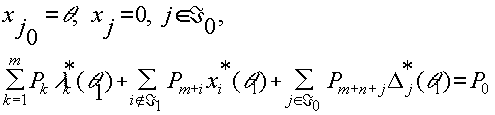
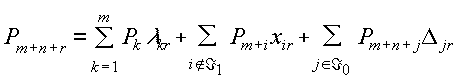
0 комментариев