Условия оптимальности в задаче (3.2)
Метод субоптимизации на многообразиях. Задача квадратичного программирования
Метод субоптимизации на многообразиях в задаче квадратичного программирования. Теоретическое обоснование
Вычислительная схема алгоритма субоптимизации для задачи квадратичного программирования
Некоторые свойства решения параметрической задачи квадратичного программирования
Навигация
Вычислительная схема алгоритма субоптимизации для задачи квадратичного программирования
Формирование инвестиционного портфеля
35791
знак
47
таблиц
18
изображений
3.7. Вычислительная схема алгоритма субоптимизации для задачи квадратичного программирования.
Ранее (см 3.4) была приведена общая схема алгоритма субоптимизации на многообразиях для случая задачи выпуклого программирования и получена блочная структура алгоритма. Конкретизируем теперь структуру блоков для случая задачи квадратичного программирования.
Блок1.
Определяется начальный набор индексов Á 1 , порождающий базис UÁ 1 , для которого оптимальная точка задачи (3.5.1) является одновременно допустимой для исходной задачи (3.1.2). Такая точка в [2] называется дополняющей.
В кочестве начального множества индексов можно взять начальный базис, получаемый в ходе решения первой фазы двухфазного симплекс-метода, или же решение задачи линейного программирования, близкой к решаемой квадратичной:
Блок 3. Блок полностью идентичен приведенному ранее в описании алгоритма субоптимизации на многообразиях для задачи выпуклого программирования.
Блок 2. В данном блоке определяется решение вспомогательной задачи (3.5.1). Способ определения решения зависит от предыдущего блока алгоритма:
Блок 2(А). Эта часть блока вступает в действие после блока 3. Оптимальный вектор задачи (3.5.1) находится с помощью операции А. Если полученный оптимальный вектор допустим для исходной задачи (3.1.2), осуществляется переход в блок 3. В противном случае осуществляется переход в блок 4.
Критерием выбора следующего шага является сравнение двух величин:
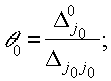
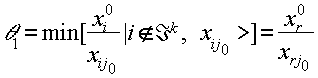
Первая величина задает момент обращения в ноль выбранной минимальной величины D j0 , вторая величина задает момент обращения в ноль первой из базисных компонент вектора x . Если вторая величина оказывается меньше первой, это означает, что новое решение задачи (3.5.1), полученное в результате операции А, не является допустимым для исходной задачи (3.1.2), и необходим переход в блок 4.
Блок 2(Б). Эта часть блока вступает в действие после блока 4. В этом блоке минимум в задаче (3.5.1) находится с помощью операции Б. Если получаемое решение оказывается допустимым для исходной задачи (3.1.2), то осуществляется переход в блок 3. В противном случае осуществляется переход в блок 4.
Критерием выбора следующего шага в этой части блока является сравнение двух величин:
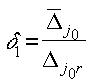
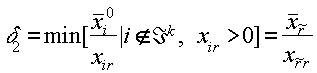
Блок 4. Этот блок полностью соответствует соответствующему блоку в общем алгоритме субоптимизации на многообразиях для задачи выпуклого программирования.
3.8. Некоторые особенности вычислительной схемы метода субоптимизации на многообразиях для задачи квадратичного программирования.
В этой части будет рассмотрен вычислительный аспект процедуры субоптимизации и показаны некоторые ее замечательные свойства.
Выше было показано, что решение каждой вспомогательной задачи метода субоптимизации сводится к поиску разложения некоторого вектора R размерности (m+n) по базису UÁ 1,Á 2 ; при этом на соседних итерациях базисы отличаются лишь каким-то одним из векторов.
Как было показано выше, существуют четыре возможных альтернативы при переходе от одного базиса к другому, задающие четыре типа операций:
1. От UÁ 1 к UÁ 2 (Á 2=Á 1 j0 ) при помощи замены в базисе вектора Pm+n+j0 на Pm+j0 .
2. От UÁ 1 к UÁ 2,Á 1 (Á 2=Á 1 j0 U r) при помощи замены в базисе вектора Pm+r на Pm+j0 .
3. От UÁ 2,Á 1 (Á 2=Á 1 j0 U r) к UÁ 2 при помощи замены в базисе вектора Pm+n+j0 на Pm+n+r .
4. От UÁ 2,Á 1 (Á 2=Á 1 j0 U r) к UÁ 2',Á 2' (Á '2=Á 2 U r', Á '1=Á 1 U r' ) при помощи замены в базисе вектора Pm+r на Pm+n+r' .
Процедура разложения вектора R по базису эквивалентна решению системы линейных уравнений вида
где B - базисная часть матрицы P (то есть матрица, составленная из столбцов матрицы P , соответствующих векторам данного базиса). Решение уравнения есть процедура, эквивалентная обращению матрицы B.
Из общего вида матрицы P (3.2.4) можно получить общий вид матрицы B, которая также имеет блочную структуру следующего вида:
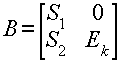
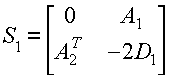
Можно показать, что
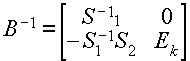
Видно, что зная матрицу S1-1 можно легко получить значение матрицы B-1 . Используя общий вид переходов, а также их общее свойство, сводящееся к замене одного вектора на другой, можно применить для нахождения S1-1 известную формулу Фробениуса, и получить рекуррентные формулы, связывающие матрицы S1-1 на соседних итерациях. Это позволяет избежать непосредственного обращения матрицы на каждом шаге алгоритма, прибегая к нему через определенный промежуток времени с целью коррекции накопившейся ошибки вычисления.
4. Задача квадратичного программирования с параметром в правых частях ограничений.
4.1 Постановка задачи
Задачей параметрического квадратичного программирования с параметром в правых частях ограничений будем называть следующую задачу выпуклого программирования:
|
| (4.1.1) |
Требуется найти вектор-функцию x*(m ) , минимизирующую целевую функцию при каждом m . Интервал изменения параметра может быть и неограниченным.
Похожие работы
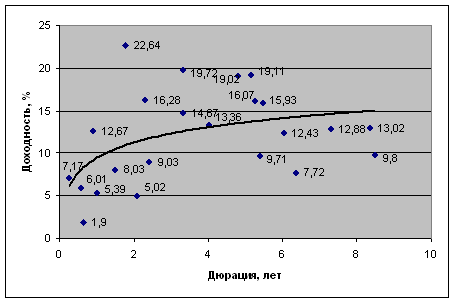
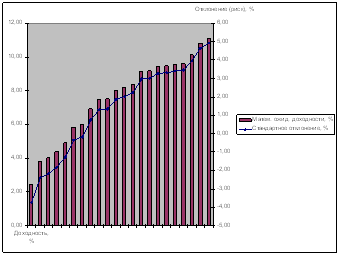
... негативных последствий для инвестиционного портфеля ОАО «МХК «ЕвроХим» и поиску путей формирования оптимальной структуры портфеля ценных бумаг организации на текущую дату. Рис. 4. Доходность еврооблигаций ОАО «МХК «ЕвроХим» на 02.03.2009 г. 3. Управление инвестиционным портфелем предприятия 3.1 Направления совершенствования структуры инвестиционного портфеля По сравнению с ...
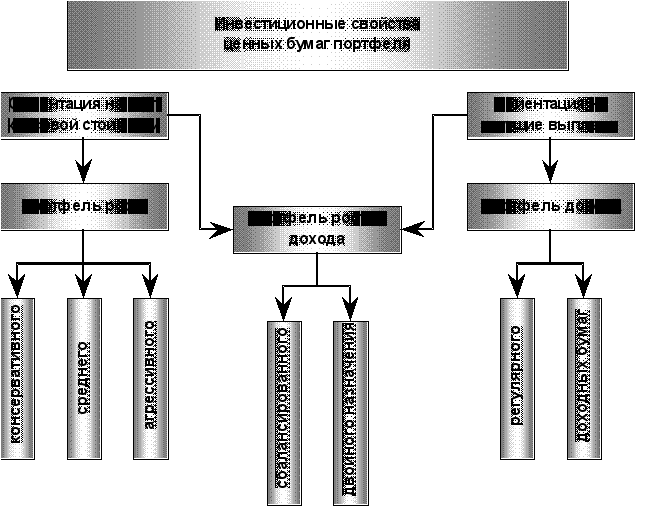
... реализацию следующих этапов: Постановка целей и выбор адекватного типа портфеля. Анализ объектов инвестирования. Формирование инвестиционного портфеля. Выбор и реализация стратегии управления портфелем. Оценка эффективности принятых решений. Первый этап включает определение целей инвестирования, способных обеспечить их достижение портфелей и необходимого объема вкладываемых средств. Следует ...
... МТС-ао 271,43 276,85 234,35 161,82 Сбербанк 72,65 65,31 44,72 31,13 Уркалий-ао 328 249,08 165,88 122,01 ГМКНорНик 5 050,91 4 917 3 379,26 1 850,28 2. Формирование инвестиционного портфеля При формировании портфеля ценных бумаг учитывается уровень ожидаемой доходности и уровень риска той или иной ценной бумаги. При расчете текущей доходности мы используем следующую формулу: ...
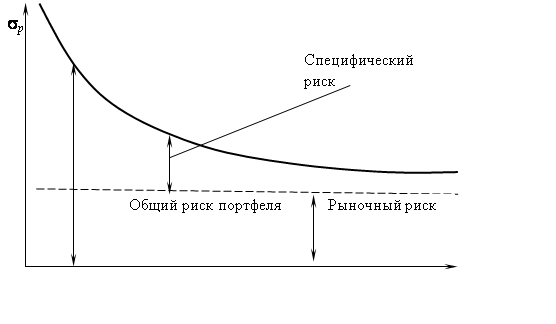
... , портфель ценных бумаг является тем инструментом, с помощью которого инвестору обеспечивается требуемая устойчивость дохода при минимальном риске. 3. ПРИНЦИПЫ ФОРМИРОВАНИЯ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ При формировании инвестиционного портфеля следует руководствоваться следующими соображениями: безопасность вложений (неуязвимость инвестиций от потрясений на рынке инвестиционного капитала), ...
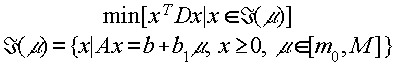
0 комментариев