Навигация
Некоторые свойства решения параметрической задачи квадратичного программирования
4.2 Некоторые свойства решения параметрической задачи квадратичного программирования.
Пусть получено решение задачи (4.1.1) при некотором значении параметра, равном m 0 . Это означает, что получен вектор x*(m 0) , а также набор индексов Á (m 0) , и порожденный им оптимальный базис. Рассмотрим множество таких m , для которых это решение остается оптимальным и допустимым. Для этого запишем условия Куна-Таккера:
|
| (4.1.2) |
Как следует из постановки задачи, правую часть выражения (4.1.2) можно представить в следующем виде:
|
| (4.1.3) |
Разложив вектор R по указанному базису, и подставив это разложение в (4.1.3), получим следующие выражения для коэффициентов разложения (4.1.2):
|
|
(4.1.4) |
Здесь ![]() - коэффициенты разложения вектора R по базису. Условием нарушения оптимальности решения является факт обращения в ноль одного из неотрицательных коэффициентов (4.1.4). Отсюда следует, что интервал, на котором исходное решение является оптимальным, является отрезком следующего вида:
- коэффициенты разложения вектора R по базису. Условием нарушения оптимальности решения является факт обращения в ноль одного из неотрицательных коэффициентов (4.1.4). Отсюда следует, что интервал, на котором исходное решение является оптимальным, является отрезком следующего вида:
|
| (4.1.5) |
где
|
|
(4.1.6) |
а
|
|
(4.1.7) |
Из выражений (4.1.4) вытекает также тот факт, что на интервалах (4.1.5) вектор-функция x*(m ) представляет собой отрезок прямой в пространстве En , и является линейной. Стало быть, значения целевой функции на интервале представляют собой параболу.
4.3 Применение метода субоптимизации на многообразиях к решению параметрической задачи квадратичного программирования.
Непосредственно из вышеизложенного следует алгоритм решения задачи квадратичного программирования с параметром в правых частях ограничений:
1. В начальной точке интервала допустимых значений параметра строится решение задачи квадратичного программирования с помощью метода субоптимизации, описанного выше.
2. С помощью формул (4.1.6-4.1.7) определяется интервал на котором полученное решение остается оптимальным.
3. В правой точке полученного интервала строится решение задачи квадратичного программирования методом субоптимизации на многообразиях. Поскольку в этой точке существуют два оптимальных базиса, с целью предотвращения зацикливания в качестве начального базиса для решения задачи предлагается использовать предыдущий оптимальный базис (если решение потеряло оптимальность) или предыдущий оптимальный базис с исключенными векторами, чьи базисные переменные обратились в ноль.
5.Экономическая часть
Рассмотрим применение описанной теории к задаче определения оптимального портфеля ценных бумаг. Сформулируем задачу:
Имеется n видов ценных бумаг, имеющих доходности выражающиеся случайными величинами ![]() , распределенными по нормальному закону с параметрами
, распределенными по нормальному закону с параметрами ![]() . Помимо этого, имеется один вид ценных бумаг, дающий гарантированную доходность
. Помимо этого, имеется один вид ценных бумаг, дающий гарантированную доходность ![]() . Некий финансист ищет такой способ вложения единицы капитала в эти ценные бумаги, который обеспечил бы максимальный уровень дохода с заданной вероятностью a .
. Некий финансист ищет такой способ вложения единицы капитала в эти ценные бумаги, который обеспечил бы максимальный уровень дохода с заданной вероятностью a .
Покажем, что указанную задачу можно свести к задаче математического программирования:
Предположим, что вектор ![]() задает вложения финансиста в ценные бумаги соответствующего типа, а величина
задает вложения финансиста в ценные бумаги соответствующего типа, а величина ![]() вложения в ценные бумаги с гарантированной доходностью. Тогда доход финансиста представляет собой случайную величину:
вложения в ценные бумаги с гарантированной доходностью. Тогда доход финансиста представляет собой случайную величину:
![]()
Очевидно, что характеристики этой случайной величины зависят от решения финансиста, и что эта величина распределена по нормальному закону:
![]()
Чтобы перейти от задачи максимизации к задаче минимизации, запишем необходимую нам функцию распределения следующим образом:
![]()
Запишем функцию квантили уровня a для этой функции распределения:
![]()
При заданном уровне a нам требуется минимизировать эту функцию, тем самым, максимизируя искомый доход R .
![]()
Для этого заметим, что случайная величина (-R) распределена также по нормальному закону с параметрами ![]() . Тогда можно записать функцию распределения этой величины, используя функцию Лапласа:
. Тогда можно записать функцию распределения этой величины, используя функцию Лапласа:
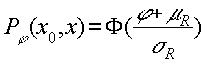
Следовательно, можно заключить, что:
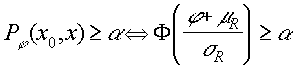
Обозначим ![]() квантиль уровня a , т.е. решение уравнения
квантиль уровня a , т.е. решение уравнения
![]()
Учитывая монотонность функции Лапласа, неравенство можно записать в следующем виде:
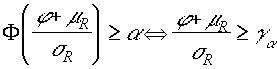
Отсюда можно легко получить выражение, дающее ключ к виду функции квантили:
![]()
Учитывая определение функции квантили:
![]()
получаем
![]()
Характеристики распределения случайной величины R выглядят следующим образом:
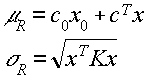
Таким образом, исходная задача сводится к следующей задаче математического программирования:
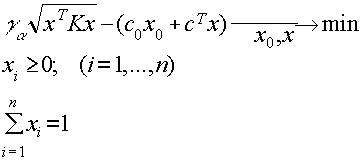
Покажем, как указанная задача математического программирования может быть сведена к задаче квадратичного программирования с параметром в правых частях ограничений:
Введем в рассмотрение параметр
![]()
Тогда задачу можно записать в следующем эквивалентном виде:
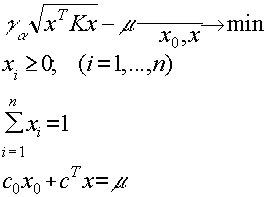
При каждом фиксированном значении параметра данная задача может быть сформулирована следующим образом:
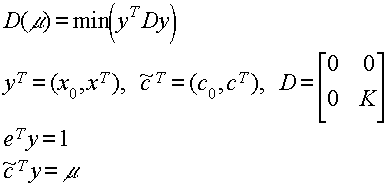
Это задача квадратичного программирования с параметром в правой части ограничений. Решая эту задачу для каждого значения параметра получаем значения функции ![]() , а, следовательно, и значения искомой минимизируемой функции
, а, следовательно, и значения искомой минимизируемой функции
![]()
Таким образом исходная задача сводится к последовательному решению двух задач - задачи квадратичного программирования с параметром в правой части ограничений и задаче одномерной оптимизации.
6.Библиография
1. Бахшиян Б.Ц., Назиров Р.Р, Эльясберг П.Е. Определение и коррекция движения (гарантирующий подход) - М.: Наука, 1980.
2. Зангвилл У.И. Нелинейное программирование. Единый подход. - М.: Советское Радио, 1973.
3. Муртаф Б. Современное линейное программирование. - М.:Мир, 1984.
4. Пропой А.И., Ядыкин А.Б. Параметрическое квадратичное и линейное программирование. - Автоматика и телемеханика, 1978, т.12, NN 2,4.
5. Хедли Дж. Нелинейное и динамическое программирование. - М.: Мир, 1967.
6. Ядыкин А.Б. Параметрический метод в задачах квадратичного программирования с вырожденной квадратичной формой. - Журнал вычислительной математики и математической физики, 1975, т.8, N4.
7. Boot J. Quadratic Programming. - Amsterdam: North-Holland Publ. Co., 1964.
8. Van de Pann C. Methods for Linear and Quadratic Programming. - Amsterdam: North-Holland Publ. Co., 1975.
Похожие работы
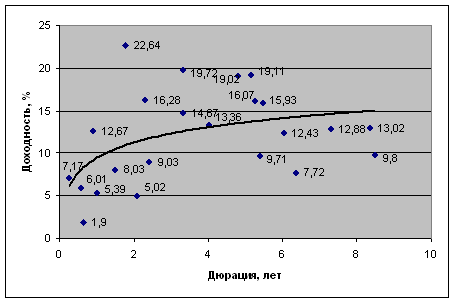
... негативных последствий для инвестиционного портфеля ОАО «МХК «ЕвроХим» и поиску путей формирования оптимальной структуры портфеля ценных бумаг организации на текущую дату. Рис. 4. Доходность еврооблигаций ОАО «МХК «ЕвроХим» на 02.03.2009 г. 3. Управление инвестиционным портфелем предприятия 3.1 Направления совершенствования структуры инвестиционного портфеля По сравнению с ...
... реализацию следующих этапов: Постановка целей и выбор адекватного типа портфеля. Анализ объектов инвестирования. Формирование инвестиционного портфеля. Выбор и реализация стратегии управления портфелем. Оценка эффективности принятых решений. Первый этап включает определение целей инвестирования, способных обеспечить их достижение портфелей и необходимого объема вкладываемых средств. Следует ...
... МТС-ао 271,43 276,85 234,35 161,82 Сбербанк 72,65 65,31 44,72 31,13 Уркалий-ао 328 249,08 165,88 122,01 ГМКНорНик 5 050,91 4 917 3 379,26 1 850,28 2. Формирование инвестиционного портфеля При формировании портфеля ценных бумаг учитывается уровень ожидаемой доходности и уровень риска той или иной ценной бумаги. При расчете текущей доходности мы используем следующую формулу: ...
... , портфель ценных бумаг является тем инструментом, с помощью которого инвестору обеспечивается требуемая устойчивость дохода при минимальном риске. 3. ПРИНЦИПЫ ФОРМИРОВАНИЯ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ При формировании инвестиционного портфеля следует руководствоваться следующими соображениями: безопасность вложений (неуязвимость инвестиций от потрясений на рынке инвестиционного капитала), ...
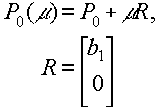
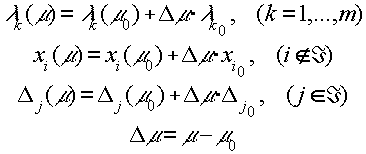
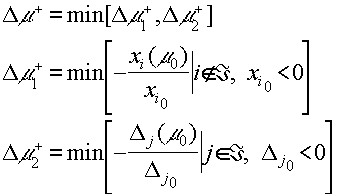
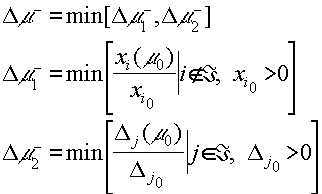
0 комментариев