Навигация
Метод субоптимизации на многообразиях в задаче квадратичного программирования. Теоретическое обоснование
3.6. Метод субоптимизации на многообразиях в задаче квадратичного программирования. Теоретическое обоснование.
Заметим, что если множество индексов Á порождает базис UÁ , то задача (3.5.1), соответствующая этому множеству индексов имеет единственный оптимальный вектор x* , обладая при этом свойством единственности, введенным ранее для задачи выпуклого программирования.
Выше были описаны вспомогательные задачи метода субоптимизации на многообразиях, однако не были сформулированы правила применения этих операций. Ниже будут доказаны две теоремы, дающие способ определения неизвестных шагов q и d . Для их доказательства потребуется несколько вспомогательных утверждений.
Лемма 1. Пусть вектора x0, x1 удовлетворяют системе уравнений условий Куна-Таккера и пусть f(x) - неотрицательно определенный квадратичный функционал вида xTDx, а D 1 вектор ограниценных по знаку множителей Лагранжа, удовлетворяющих условиям Куна-Таккера совместно с вектором x1 . Тогда имеет место следующее неравенство:
|
| (3.6.1) |
Доказательство:
Преобразуем левую часть следующим образом:
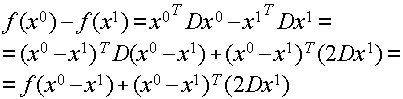
Здесь можно воспользоваться условием выполнения теоремы Куна-Таккера:
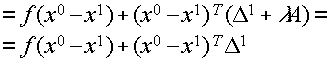
Требуемое неравенство непосредственно вытекает из последнего соотношения.
Следствие. Пусть x0, x0(q ) - оптимальные точки задачи (3.5.1) с некоторым множеством индексов Á и вспомогательной задачи поиска минимума на многообразии (3.5.4). Тогда имеет место неравенство:
![]()
Доказательство. Так как x0, x0(q ) удовлетворяют условиям Куна-Таккера, то выполняется неравенство Леммы 1:
![]()
В силу особенностей решений x0, x0(q ) правую часть неравенства можно записать в виде
![]()
что и доказывает справедливость следствия.
Лемма 2. Пусть x0, x1 - оптимальные точки многообразий XÁ 0 и XÁ 1 соответственно, удовлетворяющие условиям Куна-Таккера совместно с множителями Лагранжа D 0 и D 1. Тогда справедливо соотношение:
![]()
Доказательство: Аналогично доказательству Леммы 1, получаем, что:
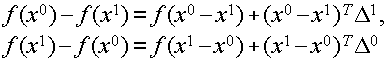
Складывая эти два равенства, получаем:
![]()
Из выполнения условий Куна-Таккера следует, что:
![]()
Раскрывая скобки в левой части неравенства получаем искомое неравенство.
Ниже будет доказана теорема, дающая направление движения и условия применения операции А.
Теорема 1. Пусть оптимальная точка x0 - оптимальная точка многообразия XÁ 0 , причем совокупность индексов Á 0 порождает базис UÁ 0 . Тогда, если среди множителей Лагранжа, соответствующих x0 , существует отрицательный (предположим, что он имеет индекс j0)
![]()
то новый набор индексов
![]()
также порождает базис ![]() и в единственной оптимальной точке
и в единственной оптимальной точке ![]() на многообразии
на многообразии ![]() выполнено условие
выполнено условие
![]()
Доказательство. Если для набора индексов ![]() существует оптимальный вектор
существует оптимальный вектор ![]() , то в силу утверждения леммы 2 и определения нового набора индексов имеем
, то в силу утверждения леммы 2 и определения нового набора индексов имеем
![]()
с другой стороны, в силу условия единственности,
![]()
Итак, если оптимальная точка на новом многообразии существует, то доказываемое неравенство верно. Существование же оптимальной точки вытекает из того факта, что новый набор индексов порождает базис. Это так, если коэффициент D j0j0 в разложении (3.5.6) не равен нулю.
Предположим, что этот коэффициент равен нулю. В этом случае, в силу следствия из леммы и условия отрицательности D j0 квадратичный функционал f(x) оказывается отрицательно определенным. Теорема доказана.
Теорема 1 указывает направление движения по многообразиям с помощью операции А. Переход от многообразия XÁ 0 к многообразию ![]() осуществляется с помощью движения по многообразиям XÁ 0 (q ) при возрастании q от нуля до некоторой величины
осуществляется с помощью движения по многообразиям XÁ 0 (q ) при возрастании q от нуля до некоторой величины
![]()
В силу вида нового множества индексов ![]() величина q 0 определяется из условия обращения в ноль соответствующего множителя Лагранжа:
величина q 0 определяется из условия обращения в ноль соответствующего множителя Лагранжа:
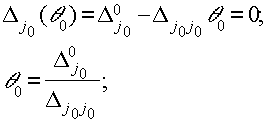
Сформулируем и докажем аналогичную теорему для операции Б:
Теорема 2. Пусть Á 0 и Á 1 наборы индексов, порождающие базис UÁ 1,Á 0 , такие, что:
![]()
причем в разложении
|
| (3.6.2) |
коэффициент ![]() . Пусть также для множества индексов
. Пусть также для множества индексов
![]()
существует оптимальный вектор ![]() для задачи (3.5.1), причем такой, что он не является допустимым для исходной задачи (3.1.2), т.е.
для задачи (3.5.1), причем такой, что он не является допустимым для исходной задачи (3.1.2), т.е.
![]()
Тогда, если x1 - оптимальная точка задачи (3.5.1) на многообразии XÁ 1 , то Á 1 порождает базис UÁ 1 , а оптимальная точка x1 принадлежит прямой (3.5.15):
|
| (3.6.3) |
Доказательство. Разложим вектор P0 по базису UÁ 1 , а вектор Pm+n+r по базису UÁ 1,Á 0 :
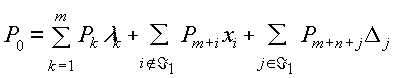
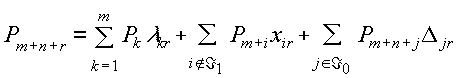
подставляя второе выражение в первое, и учитывая определение прямой (3.5.15) получаем очевидное следствие:
![]()
Кроме того, учитывая разложение (3.6.2), получаем, что
|
| (3.6.4) |
А согласно лемме 2, имеем:
![]()
Отсюда и из условия теоремы следует, что
![]()
Отсюда и из (3.6.4) вытекает доказываемое неравенство. Кроме того, из (3.6.4) также следует отличие от нуля коэффициента ![]() , что приводит к выводу о линейной независимости системы векторов UÁ 1 . Это доказывает второе утверждение теоремы.
, что приводит к выводу о линейной независимости системы векторов UÁ 1 . Это доказывает второе утверждение теоремы.
Теорема 2 указывает направление перехода от одного многообразия к другому с помощью операции Б, утверждая положительность величины шага d 1 .
Похожие работы
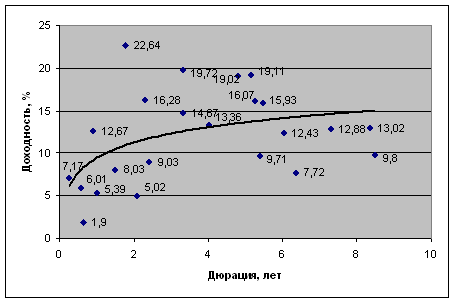
... негативных последствий для инвестиционного портфеля ОАО «МХК «ЕвроХим» и поиску путей формирования оптимальной структуры портфеля ценных бумаг организации на текущую дату. Рис. 4. Доходность еврооблигаций ОАО «МХК «ЕвроХим» на 02.03.2009 г. 3. Управление инвестиционным портфелем предприятия 3.1 Направления совершенствования структуры инвестиционного портфеля По сравнению с ...
... реализацию следующих этапов: Постановка целей и выбор адекватного типа портфеля. Анализ объектов инвестирования. Формирование инвестиционного портфеля. Выбор и реализация стратегии управления портфелем. Оценка эффективности принятых решений. Первый этап включает определение целей инвестирования, способных обеспечить их достижение портфелей и необходимого объема вкладываемых средств. Следует ...
... МТС-ао 271,43 276,85 234,35 161,82 Сбербанк 72,65 65,31 44,72 31,13 Уркалий-ао 328 249,08 165,88 122,01 ГМКНорНик 5 050,91 4 917 3 379,26 1 850,28 2. Формирование инвестиционного портфеля При формировании портфеля ценных бумаг учитывается уровень ожидаемой доходности и уровень риска той или иной ценной бумаги. При расчете текущей доходности мы используем следующую формулу: ...
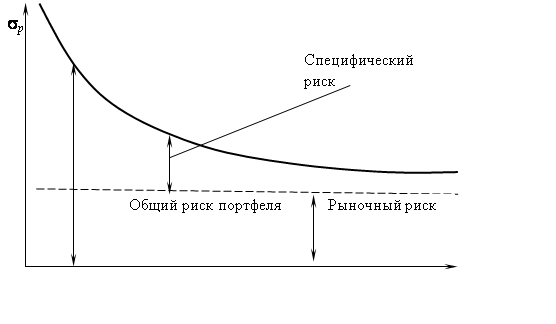
... , портфель ценных бумаг является тем инструментом, с помощью которого инвестору обеспечивается требуемая устойчивость дохода при минимальном риске. 3. ПРИНЦИПЫ ФОРМИРОВАНИЯ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ При формировании инвестиционного портфеля следует руководствоваться следующими соображениями: безопасность вложений (неуязвимость инвестиций от потрясений на рынке инвестиционного капитала), ...
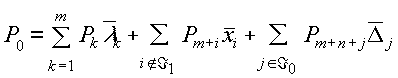
0 комментариев