ВОЛНОВЫЕ УРАВНЕНИЯ КВАНТОВОЙ МЕХАНИКИ

2. ВОЛНОВЫЕ УРАВНЕНИЯ КВАНТОВОЙ МЕХАНИКИ

Физическая теория, описывающая движение частиц, обладающих волновыми свойствами, первоначально получила название волновой механики. Однако это название вскоре было заменено другим – квантовая механика, так как оказалось, что волновая механика способна предсказывать дискретный характер или квантование различных параметров (ФВ) у движущихся микрочастиц.

Движение микрочастиц в квантовой механике описывается волновой функцией Y (x, y, z, t), подобной (1.7), но характеризующей поведение микрочастиц в трехмерном пространстве и времени. Иногда волновую функцию называют пси-функцией, по наименованию используемой для ее обозначения буквы.

Одним из постулатов квантовой механики является постулат о представлении волновой функции периодически меняющейся во времени и пространстве. Для стационарного случая волна принимается периодически меняющейся, но с неизменной плотностью распределения вероятности пространственного расположения микрочастицы.

Поскольку любая периодически меняющаяся функция может быть разложена в ряд Фурье, то волновую функцию принято описывать в суперпозиционном полигармоническом виде, приписывая каждой составляющей синусоидальный характер.

Общее временное уравнение Шредингера имеет вид

. (2.1)

Здесь – мнимая единица, а – рационализированная постоянная Планка. Стандартным символом D в (2.1) обозначен дифференциальный оператор Лапласа, который в декартовой прямоугольной системе координат определяется следующим образом:

D º . (2.2)

Уравнение Шредингера для стационарных состояний, образуемое из (2.1) при допущении, что Ψ- функция может быть представлена в виде произведения двух частей, зависящих: одна от пространственных координат, а другая от времени, имеет следующий вид

. (2.3)

Здесь малая буква ψ, в отличие от используемой в (2.1) большой буквы Ψ, обозначает лишь одну часть волновой функции, которая зависит только от пространственных координат. Вторая часть волновой функции, считающаяся находящейся в произведении с первой и здесь отсутствующая, зависит только от времени.

Почти все традиционные учебники физики, например [1, 2], говорят о невозможности выведения уравнений (2.1) и (2.3), приводя объяснение, что данные уравнения “сконструированы” или угаданы автором, точно также как в свое время были сконструированы или угаданы знаменитые уравнения Максвелла. Отдельные авторы считают, что вообще все природные закономерности устанавливаются лишь на основе опытных данных [1, стр.125].

С позиций системной взаимосвязи ФВ и системной обусловленности всех физических закономерностей, что изложено в работах автора [3-6], с таким заключением согласиться никак нельзя. Во-первых, системное и целостное представление природных закономерностей помогает формированию действительно научного мировоззрения [5, 6]. Во вторых, возможно выведение отдельных природных закономерностей привычным логическим путем. Оба эти направления необходимо раскрывать и показывать при обучении студентов физике, которую многие готовы признать - чуть ли не постулативной.

Система ФВ, варианты исполнения отдельных частей которой, применительно к рассматриваемой задаче, приведены на рис.1- рис.6, строится на упорядоченно расположенных LT- или MLT- размерностных элементах. ФВ непосредственно или с дополнительными размерностными коэффициентами многоуровнево входят в элементы системы. Закономерные взаимосвязи ФВ обнаруживаются в системе как их ближайшие системные связи или как попарное равенство произведений размерностей ФВ, располагаемых в элементах системы на противоположных вершинах выделенных параллелограммов. Более подробно эти моменты раскрыты в работе [4].

Применительно к рассматриваемой проблеме вывода волновых уравнений Шредингера следует уяснить ближайшие системные размерностные взаимосвязи ФВ действие. В системе по рис.3 и в последующих вариантах она названа действием актуальным, поскольку в квантовой механике (да и не только в ней) выявляется существование еще одного действия – это действие потенциальное, которое рассматривается чуть ниже.

Действие актуальное, квантом которого является постоянная Планка, связано через время с энергией и через длину с импульсом. В системном представлении ФВ по рис.1 - рис.4 эти связи хорошо видны.

Известна также и системно обнаруживается взаимосвязь кинетической энергии и импульса через массу микрочастицы (рассматриваем нерелятивистский случай):

. (2.4)

Далее можно идти чисто логическим путем.

Если волновая функция описывается синусоидой (или суммой синусоид), то первая производная этой функции будет косинус, который отстает по фазе от синусоиды на p /2.

Не принимая пока во внимание амплитудных и размерностных различий, мы можем установить фазовое равенство первой производной Ψ- функции по времени и ее самой, умножив эту первую производную на и приписав противоположный знак одной из сравниваемых величин.

Теперь ликвидируем размерностные отличия. Поскольку Ψ- функция от своей первой производной по времени отличается на размерность времени, то для получения размерностного равенства умножим Ψ- функцию на отношение энергии и постоянной Планка, являющейся квантом действия актуального.

Таким образом, получаем примерное размерностное соотношение:

, (2.5)

в котором W – представляет собой полную энергию, а коэффициент пропорциональности n - безразмерная числовая величина. С учетом соотношения (2.4) выражение (2.5) можно переписать в виде

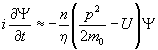, (2.6)

где в скобках фигурирует сумма кинетической и потенциальной энергий, называемая функцией Гамильтона.

Из представленной на рисунках системы (или просто из размерностных соображений) можно определить, что в выражении (2.6) импульс p можно представить - как отношение актуального действия (постоянной Планка) к длине. Коэффициент n возможно изменится, что непринципиально, а длина в минус второй степени в дифференциальных уравнениях, описывающих динамические волновые процессы, обычно представлена второй производной по направлению в пространстве (D ). Таким образом, мы логически приходим к уравнению (2.1). При этом размерность самой Ψ- функции может быть любой.

В общем случае числовой коэффициент n имеет не единственное, а множество значений, определяющих амплитуды различных гармоник Ψ- функции. Эти значения устанавливаются решением дифференциального уравнения с учетом начальных условий.

Заметим, что отношение квадрата постоянной Планка к удвоенному значению массы, представляющее по размерности произведение энергии на площадь, присутствует в правой части уравнения (2.1) вполне логично. Системные соотношения этой ФВ рассмотрены в разделе 4. В атомной физике эта величина характеризует изоэнергетическую поверхность, называемую поверхностью Ферми.

Однако использование временного уравнения Шредингера в форме выражения (2.1) не всегда может быть оправданным. Дело в том, что постоянная Планка сама представляет собой соотношение энергии с частотой (а также произведение импульса на длину волны), поэтому ее использование в формулах одновременно с указанными величинами ведет, как правило, к сильному затуманиванию в этих формулах физической сути явлений.

Если разделить обе части уравнения (2.1) на , то ситуация становится несколько яснее. Временное уравнение Шредингера принимает вид:

. (2.7)

Отношение потенциальной энергии U к постоянной Планка есть частота, а отношение постоянной Планка к массе, является физической величиной, называемой кинематической вязкостью (в термодинамике это коэффициент диффузии). Вот такие физические параметры, скорее всего, и определяют изменение пси-функции во времени.

Используя выражение (2.7) возможно осуществить простейший переход к волновому описанию стационарного состояния, что достигается приравниванием этого выражения нулю (поскольку изменения во времени принимаются отсутствующими). Сменив обозначение пси-функции на стационарное и сгруппировав одноименные величины, из (2.7) можно получить:

(2.8)

В сравнении с выражением (2.3), называемым уравнением Шредингера для стационарных состояний, здесь отсутствует (не учтена) только кинетическая энергия Е.

Если вышерассмотренным способом анализировать с самого начала выражение (2.3), то оно легко выводится из следующих логических соображений. Синусоидальная y - функция будет равна своей собственной второй пространственной производной с обратным знаком (без учета амплитудных различий), если ее умножить на квадрат отношения импульса к действию актуальному.

В действительности мы это и наблюдаем, если выражение (2.3) переписать несколько иначе:

. (2.9)

Подкоренное выражение в этой формуле представляет собой квадрат импульса, а общий коэффициент при втором члене слева (при ψ) представляет собой квадрат волнового вектора k, так что в итоге мы приходим к выводу о том, что уравнение Шредингера для стационарных состояний это обычное волновое уравнение гармонических стационарных колебаний:

. (2.10)

Если взять не вторую, как в выражении (2.10), а первую пространственную производную пси-функции, представленной в общем виде, и построить дифференциальное уравнение на сравнении этой производной с самой Ψ- функцией, то мы получим уравнение с известным в квантовой физике оператором проекции импульса (формула 3.61 учебника [1]):

. (2.11)

Из этого уравнения определяются возможные значения px. Запись последнего выражения становится более понятной с использование в уравнении волнового вектора

. (2.12)

Решением уравнения (2.12) является гармоническая функция вида

. (2.13)

Считается, что собственные значения оператора проекции импульса px образуют непрерывный спектр значений от - до + . Однако, при ограничении пси-функции по координате спектр значений волнового вектора обязательно становится дискретным. Причем получаемые дискретные значения будут целочисленно кратны основному значению, определяемому максимально возможной длиной волны (вернее ).

Исходя из представленных и ряда иных соображений, можно предположить, что используемые в квантовой механике так называемые операторы ФВ, по сути, есть искусственные образования. Они представляют собой комбинации ограниченного числа ФВ (действия актуального, энергии и импульса) с операторами дифференцирования, изымаемыми (совместно с указанными ФВ) из начальных дифференциальных уравнений, описывающих волновое представление микрочастиц.

В этой связи можно поставить под сомнение оправданность применения в квантовой механике операторов ФВ, как не имеющих физического смысла. Тем более что используются еще и операторы квадратов ФВ.

По крайней мере, с системных позиций никак не подтверждается постулат квантовой механики о том, что в ней каждой ФВ ставится в соответствие определенный оператор, а соотношения между операторами имеют ту же структуру, что и соотношения между ФВ. Построить или изобразить систему операторов ФВ, структура которой была бы подобна структуре размерностной системы самих ФВ (или имела хотя бы какой-то свой смысл), никак не получается.

Можно отметить, что применение операторного метода в квантовой механике, раз он так широко используется, видимо в какой-то мере и оправдано, например, при вычислении средних значений ФВ, хотя эти вычисления возможны и без операторов, а на основе объемной плотности распределений ФВ (раздел 8).

Похожие работы

СИСТЕМНЫЙ ПОДХОД ПРИ ИЗУЧЕНИИ ФИЗИЧЕСКОЙ КАРТИНЫ МИРА

Скачать

38044

0

0

... в различных вариантах в концепциях Дж.Чу, Х.Стаппа и Д.Бома, основано на применении организмической методологии при построении физической картины мира. Ф.Капра считает, что концепции Бома и Чу “представляют собой два наиболее изобретательных в философском отношении подхода к описанию физической действительности o2'1. Он отмечает их сближение, поскольку в последующих версиях концепции “бутстрапа” ...

Синергетика и принципы самоорганизации

Скачать

52831

0

1

... о системе. Формальные же преобразования системы сохраняют уровень ее сложности, а также качество и количество информации ("закон сохранения сложности"). Теория категорий делает явными еще 3 принципа, связанных с синергетикой 3. Принцип фрактального гомоморфизма (всеобщего подобия) фиксирует, с одной стороны, фундаментальность не того, ЧТО отражается, а КАК . . . , а с другой стороны, означает ...

Торсионные поля. Торсионные технологии

Скачать

68582

0

2

... патогенных полей, т.е. гармонизации пространства за счет применения разработанных адаптивных торсионных генераторов, “прицельно” компенсирующих и частично рассеивающих левые торсионные поля. ТОРСИОННАЯ ПОЛЯРИЗАЦИЯ ВАКУУМА. Пусть исходное пространство А¢ , соответствующее упорядоченному вакууму, деформируется внешним возмущением в пространство А¢ ¢ с отличным от нуля динамическим ...

Синергетика: различные взгляды

Скачать

413442

0

0

... мере, синергетическим стилем мышления может быть некой платформой для открытого творческого диалога между учеными, мыслителями, деятелями искусства, имеющими различные творческие установки и взгляды на мир. 2. Некоторые парадоксальные следствия синергетики Множество новых парадоксальных идей, образов и представлений возникает в синергетике. Кроме того, с точки зрения синергетики может быть ...