ВОЛНОВЫЕ УРАВНЕНИЯ КВАНТОВОЙ МЕХАНИКИ
КВАНТОВОМЕХАНИЧЕСКИЕ ПОТЕНЦИАЛЬНЫЕ ЯМЫ, ПОРОГИ И БАРЬЕРЫ ДЛЯ МИКРОЧАСТИЦ
< x <a1, 0 < y < a2, n1, n2 = 1, 2, 3, …
СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТЕЙ ГЕЙЗЕНБЕРГА, ИХ СИСТЕМНОЕ ПРЕДСТАВЛЕНИЕ И РАЗВИТИЕ
ИЗОЭНЕРГЕТИЧЕСКИЕ И ОЗОИМПУЛЬСНЫЕ ПОВЕРХНОСТИ АТОМОВ И МОЛЕКУЛ
О ФИЗИЧЕСКОЙ СУТИ ПОНЯТИЙ: ПОДВИЖНОСТЬ НОСИТЕЛЕЙ ТОКА И ПОСТОЯННАЯ ХОЛЛА
Навигация
О ФИЗИЧЕСКОЙ СУТИ ПОНЯТИЙ: ПОДВИЖНОСТЬ НОСИТЕЛЕЙ ТОКА И ПОСТОЯННАЯ ХОЛЛА
Интерпретация квантовомеханических представлений с позиций волнового описания системности физических величин
54514
знаков
1
таблица
0
изображений
7. О ФИЗИЧЕСКОЙ СУТИ ПОНЯТИЙ: ПОДВИЖНОСТЬ НОСИТЕЛЕЙ ТОКА И ПОСТОЯННАЯ ХОЛЛА
На рис.6 в системе физических величин показаны физические величины подвижность носителей тока и постоянная Холла, используемые при квантовом рассмотрении токовых явлений в физике твердого тела. Эти величины, с размерностной точки зрения, хотя и помещены на самостоятельные системные уровни, скорее всего, не являются самостоятельными ФВ. Подвижность - это величина, обратная индукции магнитного поля, а постоянная Холла – является величиной, обратной объемной плотности электрического заряда.
С физической сущностью постоянной Холла все вполне ясно. А вот уяснение обратно пропорциональной зависимости достаточно понятной величины подвижности носителей электрического тока и магнитной индукции не столь очевидно. Попробуем разобраться в этом.
Подвижность электрических зарядов (u0) в проводниках и полупроводниках определяется как отношение скорости перемещения носителей зарядов (электронов и дырок) к напряженности E0 электрического поля, вызывающего их движение.
. (7.1)
Движение электрических зарядов (величиной q) в стороннем магнитном поле с индукцией В сопровождается действием на них известной силы Лоренца:
, (7.2)
где α – угол между направлениями скорости v и индукции В.
Произведение vB sin α в этом выражении представляет собой поперечную (к основному направлению движения зарядов) составляющую напряженности электрического поля (
), обеспечивающую как раз действие на заряды поперечной силы Лоренца.
Отношение поперечной скорости перемещения электрических зарядов к указанной поперечной напряженности электрического поля () будет определять ту же подвижность электрических зарядов, поскольку подвижности как поперечная, так и продольная, вроде бы, должны быть одинаковы.
Известно, что чем больше скорость движения электрического заряда, тем больше величина индукции магнитного поля, возникающего при движении этого заряда. В нашем случае: чем больше индукция В, тем больше сила Лоренца и тем большей должна быть поперечная скорость перемещения электрических зарядов. В этом случае большее значение имеется и у поперечной составляющей электрического поля.
Поперечная составляющая электрического поля вызывает появление поперечной составляющей скорости в движении электрического заряда. Указанное движение заряда в поперечном направлении в том же магнитном поле с индукцией В вызовет (по правилу левой руки) появление как бы вторичной силы Лоренца, действующей уже прямо против основного движения заряда под действием первичного поля Е0. Таким образом, магнитное поле, внешне созданное или от собственного тока, обязательно тормозит направленное перемещение и, соответственно, ограничивает подвижность носителей электрического тока.
Не случайно, что внутри сверхпроводников, имеющих по определению бесконечно большую подвижность носителей тока, магнитного поле обязательно выталкивается вовне. Как магнитное поле связано с проводимостью обычных проводников и подвижностью носителей тока в этих проводниках - требуется еще изучать.
По всей видимости, до прояснения этого вопроса, физическую величину подвижность электрических зарядов целесообразно применять и использовать, несмотря на совершенно одинокое ее расположение в системе физических величин.
8. О ФИЗИЧНОСТИ ПРЕДСТАВЛЕНИЯ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ КВАНТОВЫХ СОСТОЯНИЙ
Устоявшиеся в квантовой механике представления о плотности распределения квантовых состояний в шестимерном фазовом пространстве с взаимно перпендикулярными осями x, y, z, px, py, pz, где полный объем состоит из произведения двух объемов - объема в пространстве координат и объема в пространстве импульсов, не очень-то понятны с физической точки зрения.
Попробуем внести ясность в эти представления на традиционном примере рассмотрения нерелятивистских электронов, находящихся в свободном состоянии.
Плотность квантовых состояний по энергии (без учета дискретности ее уровней), для единичного объема, обычно записывается в виде:
. (8.1)
В этом выражении dnE трактуется как число состояний, приходящееся в единичном объеме на интервал энергии от Е до Е + dE ([2] стр.178).
Полное число состояний, различных по энергии и находящихся в единичном объеме, равно:
. (8.2)
Последнее уравнение можно преобразовать к более простому и понятному виду:
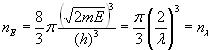. (8.3)
Выражение (8.3) показывает нам число полуволн де Бройля, содержащихся в единичном объеме. Это число, конечно же, равно числу дискретных уровней энергии или дискретных частот, содержащихся в единичном объеме. Только выражение для них будет не столь прозрачным и ясным для понимания. Прояснению ситуации несколько помогает только размерность, принимающая всегда одно и то же значение, обратное пространственному объему.
Число полуволн в единичном объеме, приходящихся на единичный интервал длины волны, определяется дифференцированием выражения (8.3)
. (8.4)
Знак минус здесь показывает увеличение плотности размещения волн с уменьшением их длины.
Формулы (8.3) и (8.4) достаточно просты для запоминания. Кроме того, с их помощью легко выводятся формулы, определяющие плотности состояний, приходящиеся на единичное значение того или иного параметра.
Для определения плотности распределений числа полуволн (частот, скоростей, импульсов и др.), приходящихся в единичном объеме на единичное значение соответствующей физической величины, требуется лишь знание взаимосвязи этих параметров с длиной волны и умение дифференцировать.
Таким путем легко выводятся следующие соотношения:
, (8.5)
, (8.6)
, (8.7)
. (8.8)
Количество отдельных уровней энергии, импульса и частот, приходящихся на единичный объем, совпадает с подобным количеством для длин волн. Это значение, выраженное через соответствующие параметры, имеет различный вид, но всегда идентично числу для длин полуволн.
, (8.9)
, (8.10)
, (8.11)
, (8.12)
В квантовой механике и статистической физике чаще всего рассматриваются энергетические распределения (8.5), объемная плотность которых, как известно, различна для классического газа и квантовых распределений из бозонов или фермионов.
Список литературы1. Мартинсон Л.К., Смирнов Е.В. Квантовая физика: Учебное пособие. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004.
2. Савельев И.В. Курс общей физики: Учеб. пособие. В 3-х томах. Т. 3. Квантовая оптика. Атомная физика. Физика твердого тела Физика атомного ядра и элементарных частиц. – 3-е изд., испр. – М.: Наука, Гл. ред. физ.-мат. лит., 1987.
3. Чуев А.С. Физическая картина мира в размерности “длина-время”. Серия “Информатизация России на пороге XXI века”. – М.: СИНТЕГ, 1999 – 96 с. (Текст книги имеется на сайте автора: http://www.chuev.narod.ru/).
4. Чуев А.С. О многоуровневой системе физических величин, выражающей законы природы, в частности, структуру и взаимосвязи электромагнитных величин. www.sciteclibrary.ru/rus/catalog/pages/7335.html . 2004.
5. Чуев А.С. О целостном подходе в преподавании естественно-научных закономерностей с использованием системы физических величин//Материалы международной научно-практической конференции "Актуальные проблемы управления - 2004". 10-11 ноября 2004 г. Выпуск 4. Москва. ГУУ-2004.
6. Чуев А.С. Преподавание и изучение природных закономерностей с использованием системы физических величин (целостный подход).//Сборник тезисов докладов Третьей Всероссийской конференции “Необратимые процессы в природе и технике”, 24-26 января 2005 г. М: МГТУ им. Н.Э. Баумана, 2
Похожие работы
... в различных вариантах в концепциях Дж.Чу, Х.Стаппа и Д.Бома, основано на применении организмической методологии при построении физической картины мира. Ф.Капра считает, что концепции Бома и Чу “представляют собой два наиболее изобретательных в философском отношении подхода к описанию физической действительности o2'1. Он отмечает их сближение, поскольку в последующих версиях концепции “бутстрапа” ...
... о системе. Формальные же преобразования системы сохраняют уровень ее сложности, а также качество и количество информации ("закон сохранения сложности"). Теория категорий делает явными еще 3 принципа, связанных с синергетикой 3. Принцип фрактального гомоморфизма (всеобщего подобия) фиксирует, с одной стороны, фундаментальность не того, ЧТО отражается, а КАК . . . , а с другой стороны, означает ...
... патогенных полей, т.е. гармонизации пространства за счет применения разработанных адаптивных торсионных генераторов, “прицельно” компенсирующих и частично рассеивающих левые торсионные поля. ТОРСИОННАЯ ПОЛЯРИЗАЦИЯ ВАКУУМА. Пусть исходное пространство А¢ , соответствующее упорядоченному вакууму, деформируется внешним возмущением в пространство А¢ ¢ с отличным от нуля динамическим ...
... мере, синергетическим стилем мышления может быть некой платформой для открытого творческого диалога между учеными, мыслителями, деятелями искусства, имеющими различные творческие установки и взгляды на мир. 2. Некоторые парадоксальные следствия синергетики Множество новых парадоксальных идей, образов и представлений возникает в синергетике. Кроме того, с точки зрения синергетики может быть ...
0 комментариев