ВОЛНОВЫЕ УРАВНЕНИЯ КВАНТОВОЙ МЕХАНИКИ
КВАНТОВОМЕХАНИЧЕСКИЕ ПОТЕНЦИАЛЬНЫЕ ЯМЫ, ПОРОГИ И БАРЬЕРЫ ДЛЯ МИКРОЧАСТИЦ
< x <a1, 0 < y < a2, n1, n2 = 1, 2, 3, …
СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТЕЙ ГЕЙЗЕНБЕРГА, ИХ СИСТЕМНОЕ ПРЕДСТАВЛЕНИЕ И РАЗВИТИЕ
ИЗОЭНЕРГЕТИЧЕСКИЕ И ОЗОИМПУЛЬСНЫЕ ПОВЕРХНОСТИ АТОМОВ И МОЛЕКУЛ
О ФИЗИЧЕСКОЙ СУТИ ПОНЯТИЙ: ПОДВИЖНОСТЬ НОСИТЕЛЕЙ ТОКА И ПОСТОЯННАЯ ХОЛЛА
Навигация
КВАНТОВОМЕХАНИЧЕСКИЕ ПОТЕНЦИАЛЬНЫЕ ЯМЫ, ПОРОГИ И БАРЬЕРЫ ДЛЯ МИКРОЧАСТИЦ
Интерпретация квантовомеханических представлений с позиций волнового описания системности физических величин
54514
знаков
1
таблица
0
изображений
3. КВАНТОВОМЕХАНИЧЕСКИЕ ПОТЕНЦИАЛЬНЫЕ ЯМЫ, ПОРОГИ И БАРЬЕРЫ ДЛЯ МИКРОЧАСТИЦ
В учебниках по квантовой механике обычно принято рассматривать примеры, описывающие поведение микрочастиц, находящихся в энергетических ямах или проходящих над (или под) энергетическими барьерами и порогами. При описании этих явлений, как правило, используются достаточно громоздкие математические формулы, из-за которых теряется физический смысл явлений.
Как пояснялось ранее, волновое уравнение Шредингера для стационарных состояний можно записать в форме (2.10) или в виде:
. (3.1)
Решением (3.1) в общем виде является функция:
. (3.2)
Для одномерной потенциальной ямы шириной а с бесконечно высокими (непроницаемыми) стенками, при использовании граничных условий 
и 
, получаем В = 0. Тогда уравнение (3.2) преобразуется в
, (3.3)
которое для А ≠ 0 формально выполняется при
, n = 0,1,2,3,… (3.4)
Последнее условие можно представить в виде
, n = 1,2,3,… (3.5)
где 
- длина волны де Бройля с чертой (
).
Выражение (3.5) имеет физический смысл – это отношение ширины потенциальной ямы к модам длин стоячих волн де Бройля, способных к существованию в этой потенциальной яме и характеризующих микрочастицу, находящуюся в яме. Это выражение показывает, что в потенциальной яме с бесконечно высокими стенками присутствуют (отбираются или резонируют) лишь моды волны, с длиной волны целочисленно дольной основной длине волны 
. Реально – половине этого значения.
Последнее выражение говорит о первоначальном квантовании в потенциальной яме длин волн или волновых векторов. Квантование уровней энергии для микрочастицы, находящейся в потенциальной яме, - это уже следствие отмеченного первоначального квантования дебройлевских длин волн.
Значит линейный или частотный спектр стоячих волн, описывающих состояние микрочастицы, находящейся в одномерной потенциальной яме с абсолютно непроницаемыми стенками, представляет собой основную длину волны (основную частоту) и бесконечно большой набор других волн, целочисленно дольных половине основной. Если же брать частоту волн де Бройля, то это основная частота и бесчисленное множество других частот, целочисленно кратных основной частоте.
Известное выражение, определяющее дискретный спектр уровней энергии микрочастицы, находящейся в одномерной потенциальной яме с бесконечно высокими стенками
, n = 1, 2, 3, … (3.6)
для понимания, лучше преобразовать и представлять в виде:
, n = 1, 2, 3, … (3.7)
Еще более понятным будет представление этого выражение в виде:
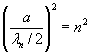, n = 1, 2, 3, … , (3.8)
откуда вытекает равенство
, n = 1, 2, 3, … , (3.9)
Последнее выражение показывает, что на ширине одномерной потенциальной ямы обязательно укладывается целое чисто дебройлевских полуволн (их гармоник), каждая из которых по частоте выше, а по длине волны меньше основной моды в целое число раз. В потенциальной яме с бесконечно высокими стенками число этих волн бесконечно большое множество. То есть, начиная с граничной частоты, имеется частотный спектр волн де Бройля. Этот спектр линейчатый и он расположен в сторону увеличения частоты до бесконечности.
Выше мы рассмотрели параметры микрочастицы, помещенной в одномерную потенциальную яму с непроницаемыми стенками. Теперь рассмотрим волновые и другие параметры для микрочастиц, находящихся в многомерных потенциальных ямах, а также в ямах, ограниченных по высоте.
Нормированная волновая функция, получаемая решением уравнения Шредингера для микрочастицы, находящейся в двумерной прямоугольной потенциальной яме с бесконечно высокими стенками, имеет вид:
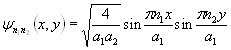, (3.10)
Похожие работы
... в различных вариантах в концепциях Дж.Чу, Х.Стаппа и Д.Бома, основано на применении организмической методологии при построении физической картины мира. Ф.Капра считает, что концепции Бома и Чу “представляют собой два наиболее изобретательных в философском отношении подхода к описанию физической действительности o2'1. Он отмечает их сближение, поскольку в последующих версиях концепции “бутстрапа” ...
... о системе. Формальные же преобразования системы сохраняют уровень ее сложности, а также качество и количество информации ("закон сохранения сложности"). Теория категорий делает явными еще 3 принципа, связанных с синергетикой 3. Принцип фрактального гомоморфизма (всеобщего подобия) фиксирует, с одной стороны, фундаментальность не того, ЧТО отражается, а КАК . . . , а с другой стороны, означает ...
... патогенных полей, т.е. гармонизации пространства за счет применения разработанных адаптивных торсионных генераторов, “прицельно” компенсирующих и частично рассеивающих левые торсионные поля. ТОРСИОННАЯ ПОЛЯРИЗАЦИЯ ВАКУУМА. Пусть исходное пространство А¢ , соответствующее упорядоченному вакууму, деформируется внешним возмущением в пространство А¢ ¢ с отличным от нуля динамическим ...
... мере, синергетическим стилем мышления может быть некой платформой для открытого творческого диалога между учеными, мыслителями, деятелями искусства, имеющими различные творческие установки и взгляды на мир. 2. Некоторые парадоксальные следствия синергетики Множество новых парадоксальных идей, образов и представлений возникает в синергетике. Кроме того, с точки зрения синергетики может быть ...
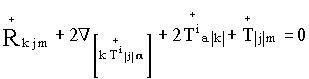
0 комментариев