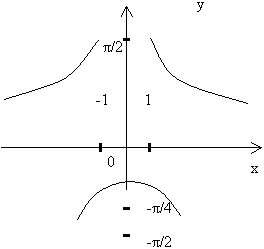
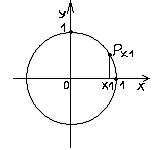
-p/2Јarcsin a Јp/2 sin(arcsin a)=a
arcsin (-a)= -arcsin a
| a | 0 | 1/2 | Ц2/2 | Ц3/2 | 1 |
| arcsin a | 0 | p/6 | p/4 | p/3 | p/2 |
x=(-1)n arcsin a +pk
| sin x=0 | x=pk |
| sin x=1 | x=p/2+2pk |
| sin x=-1 | x=-p/2+2pk |
0 Јarccos a Јp cos(arccos a)=a
arccos (-a)=p -arccos a
| a | 0 | 1/2 | Ц2/2 | Ц3/2 | 1 |
| arccos a | p/2 | p/3 | p/4 | p/6 | 0 |
x=± arccos a +2pk
| cos x=0 | x=p/2+pk |
| cos x=1 | x=2pk |
| cos x=-1 | x=p+2pk |
-p/2Јarctg a Јp/2 tg(arctg a)=a
arctg (-a)= -arctg a
| a | 0 | Ц3/3 | 1 | Ц3 |
| tg a | 0 | p/6 | p/4 | p/3 |
x=± arctg a +pk
sina*cosb=1/2[sin(a-b)+sin(a+b)]
sina*sinb=1/2[cos(a-b)-cos(a+b)]
cosa*cosb=1/2[cos(a-b)+cos(a+b)]
sina*cosb=1/2[sin(a-b)+sin(a+b)]
sina*sinb=1/2[cos(a-b)-cos(a+b)]
cosa*cosb=1/2[cos(a-b)+cos(a+b)]
sina+sinb=2sin(a+b)/2 * cos(a-b)/2
sina-sinb=2sin(a-b)/2 * cos(a+b)/2
cosa+cosb=2cos(a+b)/2 * cos(a-b)/2
cosa-cosb=-2sin(a+b)/2 * sin(a-b)/2
(a+b)2=a2+2ab+b2
(a-b)2=a2+2ab+b2
(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
a2-b2=(a-b)(a+b)
(a+b)3=a3+3a2b+3ab2+b3
(a-b)3=a3-3a2b+3ab2-b3
a3+b3=(a+b)(a2-ab+b2)
a3-b3=(a-b)(a2+ab+ b2)
| 0 | p/6 | p/4 | p/3 | p/2 | p | 2/3p | 3/4p | 5/6p | 3/2p | |
| 0 | 30° | 45° | 60° | 90° | 180 | 120° | 135° | 150° | 270° | |
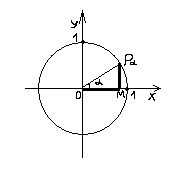
| sin | 0 | 1/2 | Ц2/2 | Ц3/2 | 1 | 0 | Ц3/2 | Ц2/2 | 1/2 | -1 |
| cos | 1 | Ц3/2 | Ц2/2 | 1/2 | 0 | -1 | -1/2 | -Ц2/2 | -Ц3/2 | 0 |
| tg | 0 | 1/Ц3 | 1 | Ц3 | - | 0 | -Ц3 | -1 | -1/Ц3 | - |
| ctg | - | Ц3 | 1 | 1/Ц3 | 0 | - | -1/Ц3 | -1 | -Ц3 | 0 |
| tg•ctg=1 cos=±Ц1-sin2 | cos(-a)=cosa | ctg(-g)=-ctga | |
| tg=1/ctg ctg=1/tg | 1+tg2=1/cos2=sec2 | ||
| sin2=(1-cos)(1+cos) | 1+ctg2=1/sin2=cosec2 | sin2a=2sina•cosa | |
| cos2=(1-sin)(1+sin) | 1-tg2/(1+tg2)=cos4-sin4 | cos2a=cos2 a-sin2 a | |
| cos/(1-sin)=1+sin/cos | 1/(tg+ctg)=sin•cos | tg2a=2tga/1-tga | |
| cos(a+b)=cosa•cosb-sina•sinb | sin3a=3sina-4sin3a | ||
| cos(a-b)=cosa•cosb+sina•sinb | cos3a=4cos3a-3cosa | ||
| sin(a+b)=sina•cosb+cosa•sinb | tg(a+b)=tga+tgb | ||
| sin(a-b)=sina•cosb-cosa•sinb | 1-tga•tgb | ||
| 2cos2a/2=1+cosa | 2sin2a/2=1-cosa |
| 0 | p/6 | p/4 | p/3 | p/2 | p | 2/3p | 3/4p | 5/6p | 3/2p | |
| 0 | 30° | 45° | 60° | 90° | 180 | 120° | 135° | 150° | 270° | |
| sin | 0 | 1/2 | Ц2/2 | Ц3/2 | 1 | 0 | Ц3/2 | Ц2/2 | 1/2 | -1 |
| cos | 1 | Ц3/2 | Ц2/2 | 1/2 | 0 | -1 | -1/2 | -Ц2/2 | -Ц3/2 | 0 |
| tg | 0 | 1/Ц3 | 1 | Ц3 | - | 0 | -Ц3 | -1 | -1/Ц3 | - |
| ctg | - | Ц3 | 1 | 1/Ц3 | 0 | - | -1/Ц3 | -1 | -Ц3 | 0 |
| tg•ctg=1 cos=±Ц1-sin2 | cos(-a)=cosa | ctg(-g)=-ctga |
sin2=(1-cos)(1+cos) 1+ctg2=1/sin2=cosec2 sin2a=2sina•cosa
cos2=(1-sin)(1+sin) 1-tg2/(1+tg2)=cos4-sin4 cos2a=cos2 a-sin2 a
| cos/(1-sin)=1+sin/cos | 1/(tg+ctg)=sin•cos | tg2a=2tga/1-tga | |
| cos(a+b)=cosa•cosb-sina•sinb | sin3a=3sina-4sin3a | ||
| cos(a-b)=cosa•cosb+sina•sinb | cos3a=4cos3a-3cosa | ||
| sin(a+b)=sina•cosb+cosa•sinb | tg(a+b)=tga+tgb | ||
| sin(a-b)=sina•cosb-cosa•sinb | 1-tga•tgb |
sin(2p-a)=-sina sin(3p/2-a)=-cosa
cos(2p-a)=cosa cos(3p/2-a)=-sina
| tg(2p-a)=-tga | tg(3p/2-a)=ctga | |
| sin(p-a)=sina | ctg(3p/2-a)=tga |
sin(p+a)=-sina cos(3p/2+a)=sina
cos(p+a)=-cosa tg(p/2+a)=-ctga
sin(p/2-a)=cosa ctg(p/2+a)=-tga
cos(p/2-a)=sina sina+sinb=2sin(a+b)/2cos(a-b)/2
| tg(p/2-a)=ctga | sina-sinb=2sin(a-b)/2*cos(a+b)/2 |
sin(p/2+a)=cosa cosa-cosb=-2sin(a+b)/2sin(a-b)/2
cos(p/2+a)=-sina
Y = C O S x
1).ООФ D(y)=R 2).ОДЗ E(y)=[-1;1]
3).Периодическая с периодом 2p
4).Чётная; cos (-x)=cos x
5).Возрастает на отрезках [-p+2pk;2pk], kОZ
Убывает на отрезках [2pk;p+2pk], kОZ
6).Наибольшее значение=1 при х=2pk, kОZ
Наименьшее значение=-1 при х=p=2pk, kОZ
7).Ноли функции х=p/2+pk, kОZ
8).MAX значение=1 х=2pk, kОZ
MIN значение=-1 х=p+2pk, kОZ
9).x>0 на отрезках [-p/2+2pk;p/2+2pk], kОZ
x<0 на отрезках [-p/2+2pk;p/2+2pk], kОZ
Y = S I N x
1).ООФ D(y)=R 2).ОДЗ E(y)=[-1;1]
3).Периодическая с периодом 2p
4).Нечётная; sin (-x)=-sin x
5).Возрастает на отрезках [-p/2+2pk;p/2+2pk], kОZ
Убывает на отрезках [p/2+2pk;3p/2+2pk], kОZ
6).Наибольшее значение=1 при х=p/2+2pk, kОZ
Наименьшее значение=-1 при х=-p/2+2pk, kОZ
7).Ноли функции х=pk, kОZ
8).MAX значение=1 х=p/2+2pk, kОZ
MIN значение=-1 х=-p/2+p+2pk, kОZ
9).x>0 на отрезках [2pk;p+2pk], kОZ
x<0 на отрезках [p+2pk;2p+2pk], kОZ
Y = T G x
1).ООФ D(y)-все, кроме х=p/2+pk kОZ
2).ОДЗ E(y)=R
3).Периодическая с периодом p
4).Нечётная; tg (-x)=-tg x
5).Возрастает на отрезках (-p/2+pk;p/2+pk), kОZ
6). Ноли функции х=pk, kОZ
7). x>0 на отрезках (pk;p/2+pk), kОZ
x<0 на отрезках (-p/2+pk;pk), kОZ
Похожие работы
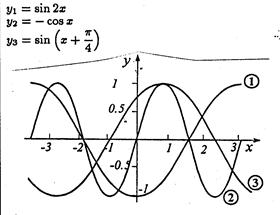
... по абсолютной величине единицы, поэтому данная функция определена для всех значений х. Преобразуем первое слагаемое по формуле (4). Приняв во внимание равенство получим: Выполнение обратных тригонометрических операций над тригонометрическими функциями. При преобразовании выражений вида следует принимать во внимание в какой четверти находится аргумент х и в каком промежутке находится значение ...
... комплект под редакцией А.Г. Мордковича, хотя оставлять без внимания остальные учебники тоже не стоит. § 3. Методика преподавания темы «Тригонометрические функции» в курсе алгебры и начал анализа В изучении тригонометрических функций в школе можно выделить два основных этапа: ü Первоначальное знакомство с тригонометрическими функциями ...
... Домашнее задание 19(3,6), 20(2,4) Постановка цели Актуализация опорных знаний Свойства тригонометрических функций Формулы приведения Новый материал Значения тригонометрических функций Решение простейших тригонометрических уравнений Закрепление Решение задач Цель урока: сегодня мы будем вычислять значения тригонометрических функций и решать ...
... математики тригонометрической подстановки и проверка эффективности разработанной методики преподавания. Этапы работы: 1. Разработка факультативного курса на тему: «Применение тригонометрической подстановки для решения алгебраических задач» с учащимися классов с углубленным изучением математики. 2. Проведение разработанного факультативного курса. 3. Проведение диагностирующей контрольной ...
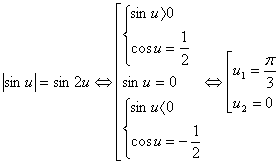
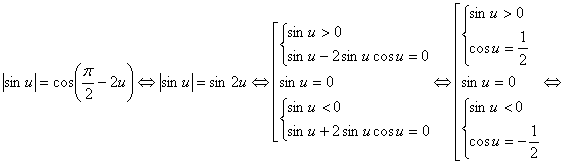

0 комментариев