Оптика

Работу выполнила Балтина Елена, 9 «А» класс

Министерство общего и профессионального образования Свердловской обл.

Управление и образование Орджоникидзевского района.

МОУ СОШ №100

Екатеринбург 2005г.

Введение:

Оптикой называется раздел физики, занимающийся изучением природы света, закономерностей его испускания, распространения и взаимодействия с веществом. Я решила написать проект по теме «Оптика», потому что в настоящее время оптика нашла свое применение во многих вопросах науки, техники и человеческой деятельности.

Геометрическая оптика §1. Экспериментальные законы.

Оптика изучает излучение, распространение и взаимодействие с веществом большого диапазона электромагнитных волн – от миллиметровых радиоволн до жесткого γ-излучения. К понятию об электромагнитной природе света люди подошли только в XIX в. Первоначально в оптике изучался видимый свет, испускаемый источниками света, - химическими, биологическими, физическими. К физическим источникам относятся раскаленные тела и люминесцентные источники холодного света. Другие тела отражают свет и потому видимы.

В оптике используются различные световые пучки – сходящиеся или расходящиеся. Достаточно узкий световой пучок, слабо сходящийся или расходящийся, назовем лучом света.

Устройство, с помощью которого преобразуются лучи, представляет собой оптическую систему. Источник лучей (собственных или отраженных) – предмет. Лучи, идущие от предмета к системе, - входящие. После преобразования в системе получаются лучи выходящие.

Оптическая система называется идеальной, если каждому входящему в нее лучу соответствует один выходящий. При этом все входящие лучи, идущие от одной точки, пересекаются (или расходятся так, что пересекаются их продолжения), выходя из системы, в одной точке. Эта точка пересечения – изображение данной точки.

Для построения изображения точки в идеальной системе достаточно построить любые два луча, идущие от этой точки. Точка пересечения выходящих лучей, соответствующих этим двум падающим, будет искомым изображением данной точки.

Лучи, выходящие из оптической системы, могут быть сходящимися или расходящимися. В первом случае они пересекутся в точке действительного изображения. Во втором – точка пересечения продолжений выходящих лучей будет мнимым изображением.

Изображение предмета в идеальной системе представляет собой совокупность изображений его точек. Это точечное изображение.

Изучая окружающий мир, человечество накопило большое количество экспериментальных сведений о свете.

Отражение и прямолинейность распространения света были известны около двух тысяч лет назад. В начале XVII в. были сформулированы законы преломления. Все это составляет предмет геометрической оптики.

Закон обратимости световых лучей. Пусть на какую-либо идеальную оптическую систему падает луч А и выходит из нее соответствующий ему луч В. Если пустить новый падающий луч навстречу В, получим новый выходящий из системы луч, идущий навстречу А.

Закон прямолинейности распространения света. В однородной среде свет распространяется прямолинейно. Мы воспринимаем источник света или предмет, от которого упал отраженный свет, на продолжении лучей, попавших в глаз. Этим законом объясняется образование геометрической тени, фотографирование камерой-обскурой (безлинзовой камерой с маленьким отверстием).

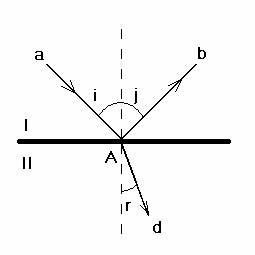
Рис.1.

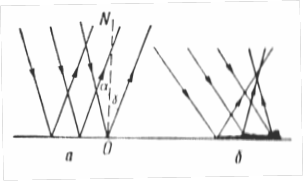
Законы отражения. Границей двух сред назовем поверхность, разделяющую две однородные среды (I и II, рис.1). Луч света, идущий к границе в среде I (которая является первой именно потому, что из нее на границу падает луч), называется падающим (а). Луч, остающийся в среде I после взаимодействия с границей в точке падения А, - отраженный (в).

Угол i между лучом падающим и перпендикуляром, восстановленным к границе двух сред в точке падения, - угол падения. Угол j между лучом отраженным и перпендикуляром к границе двух сред в точке падения – угол отражения. Плоскость, в которой лежат луч падающий и перпендикуляр к границе двух сред в точке падения, - это плоскость падения.

1. Луч падающий, перпендикуляр к границе двух сред в точке падения и луч отраженный лежат в одной плоскости. То, что две из перечисленных прямых лежат в одной плоскости, - не закон, так как любые две пересекающиеся прямые удовлетворяют этому геометрическому положению. Физическим содержанием закона является нахождение третьей прямой и той же плоскости. Следовательно, углы падения и отражения лежат в плоскости падения.

2. Угол падения равен углу отражения (изменяя произвольно угол падения, получаем такое же изменение угла отражения):

i=j. (1)

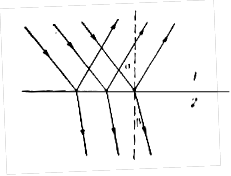
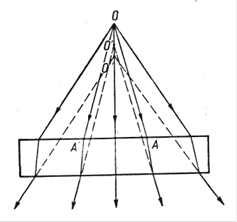
Различают отражения зеркальное и диффузное. Зеркальным называется отражение, при котором падающий на поверхность параллельный пучок лучей света остается параллельным (рис.2). Диффузным называется отражение, при котором падающий параллельный пучок рассеивается (рис.3).

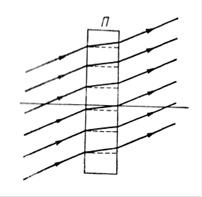
Соответственно различают зеркальные (достаточно гладкие) и матовые (рассеивающие) поверхности. Это относительные понятия. Одна поверхность может быть зеркальной и матовой для разных излучений. Даже для одного излучения матовая поверхность может стать зеркальной, если увеличить угол падения.

 

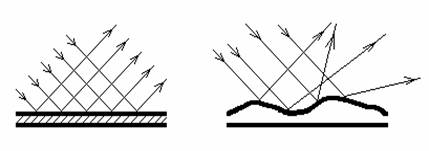
Рис.2. Рис.3.

Законы преломления. На границе двух сред кроме отражения наблюдается преломление – явление, состоящее в том, что луч частично проходит во вторую среду, изменяя свое первоначальное направление. Этот луч называется преломленным (d, рис.1). Угол r между лучом преломленным и перпендикуляром к границе двух сред в точке падения называется углом преломления.

1. Луч падающий, перпендикуляр к границе двух сред в точке падения и преломленный луч лежат в одной плоскости (аналогично первому закону отражения, смысл этого закона в том, что третья из перечисленных прямых попала в плоскость, положение которой определяют первые две. Это плоскость падения).

2. Отношение синуса угла падения к синусу угла преломления есть величина постоянная для данной пары сред (то есть не изменяется при произвольном изменении угла падения и соответственном изменении угла преломления). Эта постоянная называется показателем преломления (n21) второй среды относительно первой:

n21=sin i / sin r. (2)

Показатель преломления какой-либо среды относительно вакуума называется абсолютным показателем преломления n.

Пустим падающий на границу луч вдоль d (рис.1), преломленный луч по закону обратимости пойдет в среде I вдоль направления a. Значит (если не изменять обозначений углов),

sin r / sin i= n12=1/n21. (3)

Показатели преломления первой среды относительно второй и второй среды относительно первой – обратные величины.

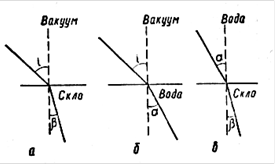
Если угол падения больше угла преломления, то вторая среда называется оптически более плотной, чем первая, и наоборот. Это определение относительно, если вторая среда оптически более плотная, чем первая, то первая среда оптически менее плотна, чем вторая. При переходе в более оптически плотную среду луч отклоняется от первоначального направления к основанию перпендикуляра, синус угла падения больше синуса угла преломления, и показатель преломления больше единицы. При переходе в оптически менее плотную среду, наоборот, показатель преломления меньше единицы.

§2. Плоское зеркало.

Рассмотрим два каких-либо луча, падающих от источника S в произвольные точки А и В плоского зеркала (рис.4). Отраженные лучи, построенные в соответствии с формулой (1), расходятся, их продолжения пересекутся в точке S1, которая будет мнимым изображением источника S (если в ней пересекутся продолжения и всех остальных отраженных лучей!).

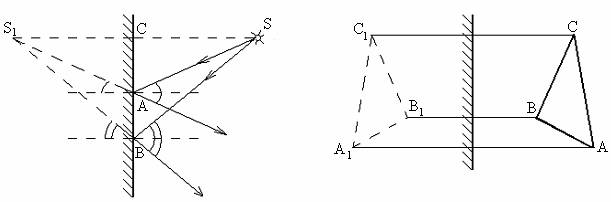 Рис.4. Рис.5.

Треугольники SAB и S1AB имеют общую сторону АВ и равные пары углов А и В [отмеченные дугой углы при точке А равны по формуле (1) и как вертикальные, аналогично равны отмеченные двумя дугами углы при точке В. Но каждый угол А в наших треугольниках равен прямому плюс один из отмеченных, значит, они раны друг другу; каждый угол В равен прямому минус отмеченные, значит, они тоже равны между собой]. Такие треугольники равны, следовательно, равны их сходственные элементы, в частности высоты, перпендикулярные зеркалу.

Следовательно, для любых треугольников SAB соответствующей высотой являются перпендикуляр к зеркалу, равный расстоянию SC, и любые лучи отразятся от зеркала так, что их продолжения пройдут через точку S1, которая и будет изображением точки S. Зеркально симметричной точкой S1 (относительно плоскости АВ) называется точка, лежащая на перпендикуляре к плоскости, опущенном из точки S на таком же расстоянии от нее: |SC| = |S1C|.

Построим изображение предмета (треугольника АВС, рис.5) в плоском зеркале. Лучи теперь можно не строить, мы знаем, что изображением каждой точки в зеркале будет зеркально симметричная точка. Изображение А1В1С1 мнимое (пересекаются продолжения лучей, нельзя получить изображение на экране, помещенное за зеркалом), прямое, равное, но зеркально симметричное (т.е. отражение левой стороны предмета являются правой стороной изображения и т. п.). Чтобы убедиться в этом, достаточно представить движение автомобилей, едущих навстречу друг другу по правой (для себя!) стороне дороги. Посмотрите в зеркало и убедитесь, что часы у вашего изображения на правой руке и т. д. Отпечаток текста на промокательной бумаге читается с трудом – там буквы «наоборот». В зеркале изображение еще раз переворачивается и читается легко.

§3. Сферические зеркала.

Из всех неплоских зеркал мы рассмотрим только сферические, отражающая поверхность которых представляет собой внешнюю или внутреннюю часть сферы. Имеем вогнутое зеркало (рис.6). Середина С зеркала называется полюсом.

 

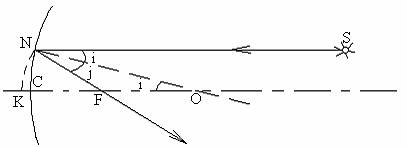
Рис.6.

Любой луч, упавший на зеркало через центр сферы (угол падения равен нулю), отразившись, пойдет по тому же направлению. Существует только одна точка О, удовлетворяющая этому условию. Она называется оптическим центром зеркала. Все прямые, проходящие через оптический центр, - оптические оси зеркала. Одна из оптических осей проходит через полюс С зеркала, это главная оптическая ось. Остальные оптические оси – побочные.

Пусть на зеркало в точку N падает луч, параллельный главной оптической оси. NO – радиус и, следовательно, перпендикуляр к сфере. Построив угол отражения равным углу падения, получим отраженный луч NF. Углы падения i и NOF равны, как внутренние накрест лежащие при параллельных прямых и секущей. Следовательно, треугольник NOF – равнобедренный, и ׀NF׀=׀FO׀.

Проведем дугу NK радиусом FN. Точка пересечения дуги с главной оптической осью не совпадает с точкой С, но близка к ней. Отрезок ׀СК׀ тем меньше, чем ближе SN к главной оптической оси. Ограничимся только параксиальными (приосевыми) пучками, с тем чтобы можно было считать пренебрежимо малым отрезок ׀СК׀«׀CF׀. Для таких пучков ׀CF׀=׀NF׀=׀FO׀, и точка F для всех параксиальных лучей лежит посередине радиуса СО. Эта точка называется главным фокусом зеркала (разумеется, есть фокусы и на всех остальных оптических осях – побочные). Итак, главный фокус вогнутого зеркала – точка, в которой после отражения пересекутся все параксиальные лучи, падающие параллельно главной оптической оси.

Аналогичные рассуждения и построения приведут нас к понятию мнимого главного фокуса выпуклого зеркала (рис.7). Расстояние от зеркала до главного фокуса называется фокусным расстоянием и обозначается F. Можно доказать, что все падающие из одной точки лучи после отражения от вогнутого зеркала проходят через одну точку – изображение (доказать это можно хотя бы построением; из-за приблизительности условия параксиальности это, конечно, не совсем точка, а небольшое пятно, для выпуклого зеркала – это точка пересечения продолжений всех отраженных лучей). Для построения такой точки достаточно каких-нибудь двух лучей. Луч, падающий параллельно главной оптической оси, после отражения пройдет через главный фокус (или продолжение отраженного луча пройдет через главный фокус – для выпуклого зеркала). По закону обратимости, луч, падающий через главный фокус, после отражения пойдет параллельно главной оптической оси. Наконец, луч, падающий через центр сферы, отразится по тому же направлению.

 

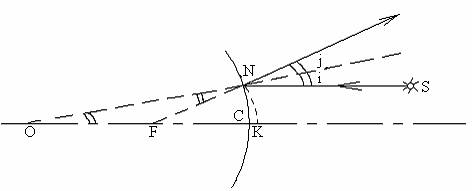
Рис.7.

При построении изображения точки в вогнутом зеркале (рис.8) намечают точки O, F, C, затем строят любые два из трех перечисленных лучей. Через точку пересечения отраженных лучей S1 пройдут и все остальные отраженные лучи – она является действительным изображением точки S. Построение изображения в выпуклом зеркале аналогично.

 

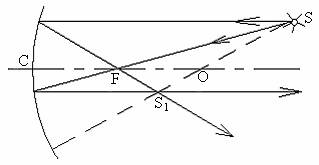
Рис.8.

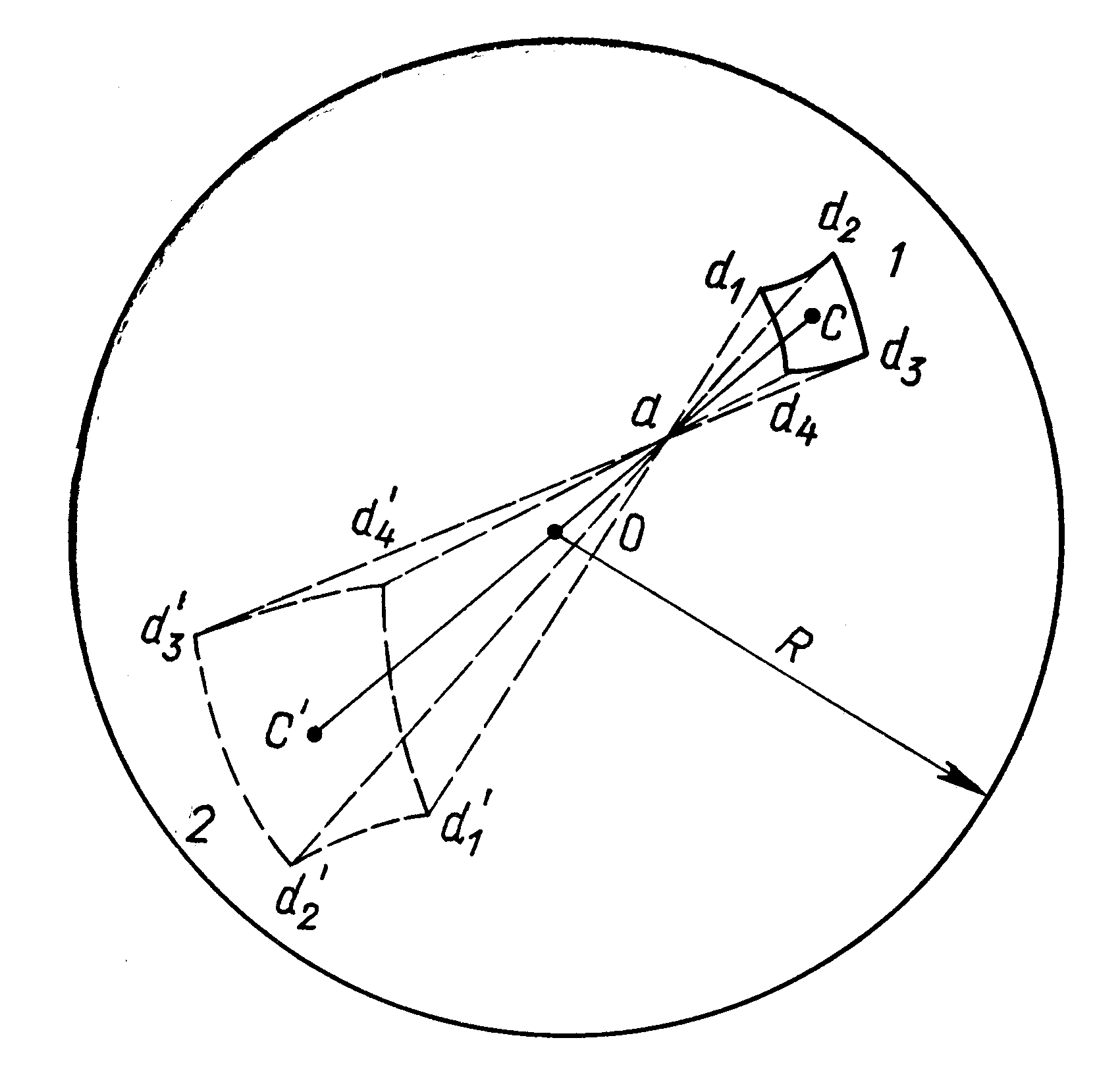
Построим изображение предмета АВ в вогнутом зеркале (рис.9). Изображение А1 находим, как на рис.8. Построение изображения точки, расположенной на главной оптической оси, осуществляется так: проводим произвольный луч ВМ и параллельно ему соответствующую побочную ось OD; на середине расстояния OD расположен побочный фокус F1, через который пройдет отраженный от точки М луч. В качестве второго луча удобно выбрать луч, идущий вдоль главной оптической оси. Точка пересечения двух отраженных лучей – изображение В1.

 

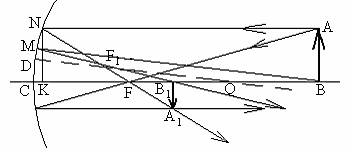
Рис.9.

Обозначим расстояние от зеркала до предмета d=׀СВ׀; расстояние от зеркала до изображения f=|СB1|; фокусное расстояние F=׀CF׀≈׀KF׀. Из подобия треугольников А1В1F и NKF следует равенство

|A1B1|/|AB|=(f – F)/F;

аналогично, из подобия треугольников А1В1О и АВО

|A1B1|/|AB|=(2F – f)/(d – 2F).

Отсюда (f – F)/F=(2F – f)/(d – 2F).

2F2 – Ff=fd – Fd – 2Ff + 2F2

fF + Fd=fd

Разделим это уравнение на произведение Ffd:

 (4)

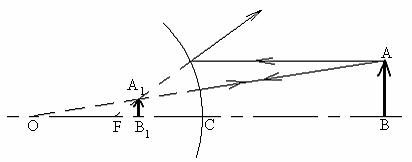
Рис.10.

Мы получили формулу зеркала. Ее можно применять и к выпуклому зеркалу. Аналогичное построение для выпуклого зеркала (рис. 10) показывает, что если предмет расположен перед зеркалом (d>0), то изображение расположено по другую сторону зеркала (f<0) и фокус находится за зеркалом (F<0). Если взять все величины по модулю, то формула выпуклого зеркала примет вид

 или .

Это же выражение можно получить из подобия треугольников на рис. 10.

Линейным увеличением зеркала называется отношение линейных размеров изображения и предмета:

k = |A1B1|/|AB|.

Это отношение из подобия треугольников NKF и FA1B1 (рис. 9):

.

Следовательно, линейное увеличение

. (5)

Исследуем формулу вогнутого зеркала. Для этого найдем из нее расстояние от изображения до зеркала:

.

1.Пусть предмет расположен в бесконечности, то есть от него идут только лучи, параллельные главной оптической оси. Тогда d = ∞,

 .

Изображение в главном фокусе, действительное, уменьшенное (точка).

2. Предмет на конечном расстоянии за центром сферы: 2F < d < ∞. Тогда

.

Изображение между центром и фокусом зеркала, действительное, обратное, уменьшенное.

4. Предмет между фокусом и центром зеркала: F < d < 2F. Значит,

.

Изображение действительное, обратное, увеличенное, расположено за центром зеркала.