Навигация
Определение: эксцентриситет – величина равная отношению с к а
1. Определение: эксцентриситет – величина равная отношению с к а.
е=с/а
е эллипсв <1 (т.к. а>c)
е гиперболы >1 (т.к. с>a)
Определение: окружность – эллипс у которого а=b, с=0, е=0.
Выразим эксцентриситеты через а и b:
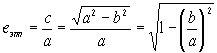
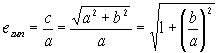
е эллипса является мерой его “вытянутости”
е гиперболы характеризует угол раствора между асимптотами
2. Директрисой D эллипса (гиперболы), соответствующей фокусу F, называется прямая расположенная в полуплоскости a перпендикулярно большой оси эллипса и отстоящий от его центра на расстоянии а/е>a (а/е<a)
D1: x= - a/e
D2: x= a/e
р=а(1-е2)/е – для эллипса
р=а(е2-1)/е – для гиперболы
ТЕОРЕМА ОБ ОТНОШЕНИИ РАССТОЯНИЙ. 2-ОЕ ОПРЕДЕЛЕНИЕ ЭЛЛИПСА, ГИПЕРБОЛЫ, ПАРАБОЛЫ.
Теорема: Отношение расстояния любой точки эллипса (гиперболы) до фокуса к расстоянию от нее до соответствующей директрисы есть величина постоянная равная е эллипса (гиперболы).
Доказательство: для эллипса.
r1/d1=e
![]() x£ |a|, xe+a>0
x£ |a|, xe+a>0
r1=xe+a
d1 – расстояние от М(x,y) до прямой D1
xcos180+ysin180-p=0
x=-p
x=-a/e
бм=-x-a/e
d1=-бм (минус, т.к. прямая и точка по одну стороно о начала коорд.)
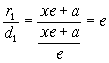
Определение: ГМТ на плоскости, отношение расстояния от которых до фокуса, к расстоянию до соответствующей директрисы есть величина постоянная и представляет собой эллипс, если <1, гиперболу, если >1, параболу, если =1.
ПОЛЯРНОЕ УРАВНЕНИЕ ЭЛЛИПСА, ГИПЕРБОЛЫ, ПАРАБОЛЫ.
Пусть задан эллипс, парабола или правая ветвь гиперболы.
Пусть задан фокус этих кривых. Поместим полюс полярной системы в фокус кривой, а полярную ось совместим с осью симметрии, на которой находится фокус.
r= r
d=p+r cosj
e=r /p+r cosj
![]() - полярное уравнение эллипса, параболы и правой ветви гиперболы.
- полярное уравнение эллипса, параболы и правой ветви гиперболы.
КАСАТЕЛЬНАЯ К КРИВОЙ 2-ГО ПОРЯДКА.
Пусть задан эллипс в каноническом виде. Найдем уравнение касательной к нему, проходящей через М0(x0;y0) – точка касания, она принадлежит эллипсу значит справедливо:
![]()
у-у0=y’(x0)(x-x0)
![]()
Рассмотрим касательную к кривой ![]() следовательно
следовательно ![]()
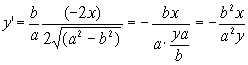
![]()
![]()
ya2y0-a2y02+b2x0x-b2x02=0
![]()
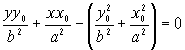
![]() - уравнение касательной к эллипсу.
- уравнение касательной к эллипсу.
![]() - уравнение касательной к гиперболе.
- уравнение касательной к гиперболе.
![]() - уравнение касательной к параболе.
- уравнение касательной к параболе.
ПРЕОБРАЗОВАНИЕ ДЕКАРТОВЫХ ПРЯМОУГОЛЬНЫХ КООРДИНАТ НА ПЛОСКОСТИ.
Преобразование на плоскости есть применение преобразований параллельного переноса и поворота.
Пусть две прямоугольные системы координат имеют общее начало. Рассмотрим все возможные скалярные произведения базисных векторов двумя способами:
(е1;е1’)=cos u
(е1;е2’)=cos (90+u)= -sin u
(е2;е1’)=cos (90-u)=sin u
(е2;е2’)=cos u
Базис рассматривается ортонормированный:
(е1;е1’)=(е1, a 11е1+a 12е2)= a 11
(е1;е2’)= (е1, a 21е1+a 22е2)= a 21
(е2;е1’)= a 12
(е2;е2’)= a 22
Приравниваем:
a 11=cos u
a 21= - sin u
a 12=sin u
a 22=cos u
Получаем:
x=a+x’cos u – y’sin u
y=b+x’sin u – y’cos u - формулы поворота системы координат на угол u.
------------
x=a+x’
y=b+y’ - формулы параллельного переноса
ИНВАРИАНТЫ УРАВНЕНИЯ ЛИНИЙ 2-ГО ПОРЯДКА.
Определение: Инвариантой ур-я (1) линии второго порядка относительно преобразования системы координат, называется функция зависящая от коэффициентов ур-я (1) и не меняющая своего значения при преобразовании системы координат.
Теорема: инвариантами уравнения (1) линии второго порядка относительно преобразования системы координат являются следующие величины: I1; I2; I3
Вывод: при преобразовании системы координат 3 величины остаются неизменными, поэтому они характеризуют линию.
Определение:
I2>0 – элиптический тип
I2<0 – гиперболический тип
I2=0 – параболический тип
ЦЕНТР ЛИНИИ 2-ГО ПОРЯДКА.
Пусть задана на плоскости линия уравнением (1).
Параллельный перенос:
Параллельно перенесем систему XOY на вектор OO’ т.о. что бы в системе X’O’Y’ коэфф. при x’ и y’ преобразованного уравнения кривой оказались равными нулю. После этого:
a11x’2+2a12x’y’+a22y’2+a’33=0 (2)
точка О’ находится из условия: a13’=0 и a23’=0.
Получается система a11x0+a12y0+a13=0 и a12x0+a22y0+a23=0
Покажем, что новое начало координат (если система разрешима) является центром симметрии кривой: f(x’;y’)=0, f(-x’;-y’)= f(x’;y’)
Но точка О’ существует если знаменатели у x0 и y0 отличны от нуля.
Точка O’ – единственная точка.
Центр симметрии кривой существует если I2¹ 0 т.е. центр симметрии имеют линии элиптического и гиперболического типа
Поворот:
Пусть система XOY повернута на угол u. В новой системе координат уравнение не содержит члена с x’y’ т.е. мы делаем коэфф. а12=0. a12’= -0,5(a11-a22)sin2u+a12cos2u=0 (разделим на sin2u), получим:
![]() , после такого преобразования уравнение принимает вид
, после такого преобразования уравнение принимает вид
a11’x’2+a22’y’2+2a13’x’+2a23’y’+a33’=0 (3)
ТЕОРЕМА О ЛИНИЯХ ЭЛИПТИЧЕСКОГО ТИПА.
Теорема: Пусть задана линия элиптического типа т.е. I2>0 и пусть I1>0 следовательно уравнение (1) определяет: 1. I3<0 – эллипс; 2. I3=0 – точка; 3. I3>0 – ур-е (1) не определяет. Если I3=0 говорят, что эллипс вырождается в точку. Если I3>0 говорят, что задается мнимый эллипс. Пусть после ПП и поворота ур-е (1) принимает вид (*).
Доказательство:
1. пусть I2>0, I1>0, I3<0, тогда
а11’’x’’2+a22’’ y’’2= -I3/I2
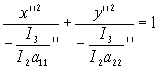
I2=a11’’a22’’ > 0
I1= a11’’+a22’’ > 0
a11’’ > 0; a22’’ > 0
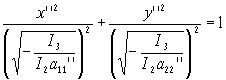
Итак, под корнями стоят положительные числа, следовательно, уравнение эллипса.
Похожие работы
... поверхность второго порядка определяет следующее уравнение: 4x2 – y2 – z2 – 4xz =2? Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ Билет № 26 121. Напишите условие параллельности прямых на плоскости, заданных уравнениями с угловыми ...
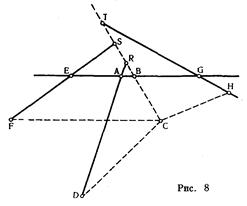
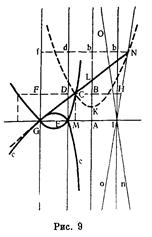
... котором четыре прямые суть эквидистанты АВ, IH, ED, GF, а пятая GA к ним перпендикулярна (рис. 9), причем CF·CD·CH = СВ·СМ·а, где а — расстояние между соседними эквидистантами. Здесь появляется первое в истории аналитической геометрии уравнение кривой третьего порядка. Обозначив СВ = у, СМ = х, Декарт находит у3 — 2ay2 — аау + 2а3 = аху, т. е. уравнение трезубца (см. стр. 106), и показывает, что ...
... образ математики, сыгравший формирующую, заправляющую роль. Из математики исламской культуры приходит подчеркнутое пристрастие к алгоритмическим методам, к знанию, сформулированному в виде правил и рецептов. Декарт, демонстрируя в своей книге мощь нового метода аналитической геометрии, существенно преакцинтирует само понимание геометрии - и в смысле метода, и в смысле предмета. Причины этой ...
... в отношении , то координаты точки следующие: . Пример 5. Найти точку , делящую отрезок в отношении , если . Решение. Определим координаты точки : . Таким образом, . Аналитическая геометрия. Уравнение плоскости. Общее уравнение плоскости имеет вид: , , где – нормальный вектор плоскости (т.е. перпендикулярный плоскости), а коэффициент пропорционален расстоянию от начала координат ...

0 комментариев