Навигация
I3>0 в данном случае под корнем стоят отрицательные числа, следовательно уравнение не определяет действительного геометрического образа
2. I3>0 в данном случае под корнем стоят отрицательные числа, следовательно уравнение не определяет действительного геометрического образа.
3. I3=0 в данном случае т(0,0) – случай вырождения эллипса.
ТЕОРЕМА О ЛИНИЯХ ГИПЕРБОЛИЧЕСКОГО ТИПА.
Теорема: Пусть уравнение (1) определяет линию гиперболического типа. Т.е. I2<0, I3¹ 0 - ур-е (1) определяет гиперболу; I3=0 – пару пересекающихся прямых.
Доказательство: I2<0; I2= a11’’a22’’ < 0. Пусть a11’’>0; a22’’<0
Пусть I3>0
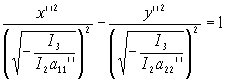
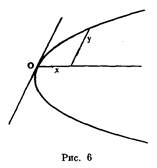
В данном случае мы имеем гиперболу с действительной осью ОХ.
Пусть I3<0
-(-а11’’)x’’2+a22’’ y’’2= -I3/I2
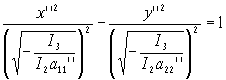
В этом случае мы имеем гиперболу с действительной осью ОY
Пусть I3=0
а11’’x’’2-(-a22’’)y’’2=0
![]()
![]()
АСИМПТОТИЧЕСКИЕ НАПРАВЛЕНИЯ КРИВЫХ 2-ГО ПОРЯДКА.
Пусть крива второго порядка задана уравнением (1). Рассмотрим квадратную часть этого уравнения: u(x,y)= a11x2+2a12xy+a22y2
Определение: ненулевой вектор (a , b ) координаты которого обращают в ноль квадратичную часть называется вектором асимптотического направления заданной кривой.
(a , b ) – вектор асимптотического направления.
a11a 2+2a12a b +a22b 2=0 (*)
Рассмотрим (a ’, b ’) параллельный (a , b ): ![]() следовательно
следовательно ![]() . Дробь a /b характеризует вектор асимптотического направления.
. Дробь a /b характеризует вектор асимптотического направления.
Задача: выяснить какие асимптотические направления имеют кривые 2-го порядка.
Решение: положим, что b ¹ 0 и поделим на b 2, получим: a11(a /b )2+2a12a /b +a22=0 из этого квадратного уравнения найдем a /b .
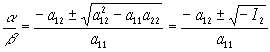
т.к. у линий гиперболического и параболического типов I2£ 0, то они имеют асимптотические направления. Т.к. у эллипса I2>0 следовательно таких у него нет (говорят он имеет мнимые асимптотические направления).
Найдем асимптотические направления у гиперболы:
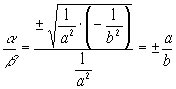
(a , b )1=(a,b)
(a , b )2=(-a,b)
Векторы асимптотического направления являются направляющими векторами для асимптот.
Итак: гипербола имеет два асимптотических направления, которые определяются асимптотами гиперболы.
Найдем асимптотические направления у параболы:
y2=2px
y2-2px=0
u(x,y)= y2+0, y=0
(a , b )=(0,0)
Итак: вектор асимптотического направления параболы лежит на оси симметрии параболы, т.е. прямая асимптотического направления пересекает параболу в одной точке, след. асимптотой не является. Парабола имеет одно асимптотическое направление, но асимптот не имеет.
РАЗЛИЧНЫЕ УРАВНЕНИЯ ПЛОСКОСТИ.
Пусть задано трехмерное пространство.
Теорема: Плоскость в афинной системе координат задается уравнением первой степени от трех переменных: Ax+By+Cz+D=0, где A,B,C¹ 0 одновреенно. Справедлива и обратная теорема.
Теорема: Вектор n(A, B, C) ортоганален плоскости, задаваемой общим уравнением.
Вектор n – нормальный вектор плоскости.
2. Уравнение плоскости в отрезках: ![]()
3. Уравнение плоскости, определенной нормальным вектором и точкой.
Пусть n(A,B,C) и М(x0;y0;z0). Запишем ур-е пл-ти:
Ax+By+Cz+D=0
Ax0+By0+Cz0=-D
A(x-x0)+B(y-y0)+C(z-z0)=0
Уравнение плоскости ч/з 3 точки.
Пусть известны три точки не принадл. одной прямой.
М1(x1;y1;z1); М2(x2;y2;z2); М3(x3;y3;z3)
Пусть М(x;y;z) – произвольная точка плоскости. Т.к. точки принадл. одной плоскости то векторы компланарны.
М1М x-x1 y-y1 z-z1
М1М2 x2-x1 y2-y1 z2-z1 =0
М1М3 x3-x1 y3-y1 z3-z1
Параметрическое ур-е плоскости.
Пусть плоскость определена точкой и парой некомпланарных векторов. V(V1;V2;V3); U(U1;U2;U3); M0(x0;y0;z0), тогда плостость имеет вид: система: x=x0+V1t+U1s и y=y0+V2t+U2s и z=z0+V3t+U3s
РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ.
Ax+By+Cz+D=0; M0(x0;y0;z0)
![]()
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ В ПРОСТРАНСТВЕ.
Угол между плоскостями: пусть заданы две плоскости: A1x+B1y+C1z+D1=0; A2x+B2y+C2z+D2=0, поэтому n1(A1;B1;C1); n2(A2;B2;C2). Отыскание угла между плоскостями сводится к отысканию его между нормальными векторами.
![]()
Похожие работы
... поверхность второго порядка определяет следующее уравнение: 4x2 – y2 – z2 – 4xz =2? Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ Билет № 26 121. Напишите условие параллельности прямых на плоскости, заданных уравнениями с угловыми ...
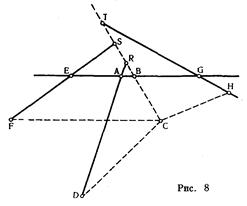
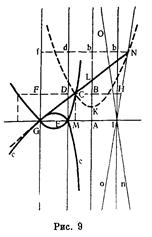
... котором четыре прямые суть эквидистанты АВ, IH, ED, GF, а пятая GA к ним перпендикулярна (рис. 9), причем CF·CD·CH = СВ·СМ·а, где а — расстояние между соседними эквидистантами. Здесь появляется первое в истории аналитической геометрии уравнение кривой третьего порядка. Обозначив СВ = у, СМ = х, Декарт находит у3 — 2ay2 — аау + 2а3 = аху, т. е. уравнение трезубца (см. стр. 106), и показывает, что ...
... образ математики, сыгравший формирующую, заправляющую роль. Из математики исламской культуры приходит подчеркнутое пристрастие к алгоритмическим методам, к знанию, сформулированному в виде правил и рецептов. Декарт, демонстрируя в своей книге мощь нового метода аналитической геометрии, существенно преакцинтирует само понимание геометрии - и в смысле метода, и в смысле предмета. Причины этой ...
... в отношении , то координаты точки следующие: . Пример 5. Найти точку , делящую отрезок в отношении , если . Решение. Определим координаты точки : . Таким образом, . Аналитическая геометрия. Уравнение плоскости. Общее уравнение плоскости имеет вид: , , где – нормальный вектор плоскости (т.е. перпендикулярный плоскости), а коэффициент пропорционален расстоянию от начала координат ...

0 комментариев