Навигация
Непрерывные генетические алгоритмы
33080
знаков
5
таблиц
4
изображения
3. Непрерывные генетические алгоритмы.
Фиксированная длина хромосомы и кодирование строк двоичным алфавитом преобладали в теории генетических алгоритмов с момента начала ее развития, когда были получены теоретические результаты о целесообразности использования именно двоичного алфавита. К тому же, реализация такого генетического алгоритма на ЭВМ была сравнительно легкой. Все же, небольшая группа исследователей шла по пути применения в генетических алгоритмах отличных от двоичных алфавитов для решения частных прикладных задач. Одной из таких задач является нахождение решений, представленных в форме вещественных чисел, что называется не иначе как «поисковая оптимизация в непрерывных пространствах». Возникла следующая идея: решение в хромосоме представлять напрямую в виде набора вещественных чисел. Естественно, что потребовались специальные реализации биологических операторов. Такой тип генетического алгоритма получил название непрерывного генетического алгоритма (RGA, или real-coded genetic algorithm), или генетического алгоритма с вещественным кодированием.
Первоначально непрерывные гены стали использоваться в специфических приложениях (например, хемометрика, оптимальный подбор параметров операторов стандартных генетических алгоритмов и др.). Позднее они начинают применяться для решения других задач оптимизации в непрерывных пространствах (работы исследователей Wright, Davis, Michalewicz, Eshelman, Herrera в 1991-1995 гг). Поскольку до 1991 теоретических обоснований работы непрерывных генетических алгоритмов не существовало, использование этого нового подвида было спорным; ученые, знакомые с фундаментальной теорией эволюционных вычислений, в которой было доказано превосходство двоичного алфавита перед другими, критически воспринимали успехи алгоритмов с вещественным кодированием. После того, как спустя некоторое время теоретическое обоснование появилось, непрерывные генетические алгоритмы полностью вытеснили двоичные хромосомы при поиске в непрерывных пространствах.
Преимущества и недостатки двоичного кодирования
Прежде чем излагать особенности математического аппарата непрерывных генетических алгоритмов, остановимся на анализе достоинств и недостатков двоичной схем кодирования.
Как известно, высокая эффективность отыскания глобального минимума или максимума генетическим алгоритмом с двоичным кодированием теоретически обоснована в фундаментальной теореме генетических алгоритмов («теореме о шаблоне»), доказанной Холландом. Ее суть в том, что двоичный алфавит позволяет обрабатывать максимальное количество информации по сравнению с другими схемами кодирования.
Однако двоичное представление хромосом влечет за собой определенные трудности при поиске в непрерывных пространствах большой размерности, и когда требуется высокая точность найденного решения. В генетических алгоритмах с двоичным кодированием для преобразования генотипа в фенотип используется специальный прием, основанный на том, что весь интервал допустимых значений признака объекта 
разбивается на участки с требуемой точностью. Заданная точность p определяется выражением
где N – количество разрядов для кодирования битовой строки.
Эта формула показывает, что p сильно зависит от N, т.е. точность представления определяется количеством разрядов, используемых для кодирования одной хромосомы. Поэтому при увеличении N пространство поиска расширяется и становится огромным.
Известный книжный пример: пусть для 100 переменных, изменяющихся в интервале 
, требуется найти экстремум с точностью до шестого знака после запятой. В этом случае при использовании генетических алгоритмов с двоичным кодированием длина строки составит 3000 элементов, а пространство поиска – около 
хромосом.
Эффективность генетических алгоритмов с двоичным кодированием в этом случае будет невысокой. На первых итерациях алгоритм потратит много усилий на оценку младших разрядов числа, закодированных во фрагменте двоичной хромосомы. Но оптимальное значение на первых итерациях будет зависеть от старших разрядов числа. Следовательно, пока в процессе эволюции алгоритм не выйдет на значение старшего разряда в окрестности оптимума, операции с младшими разрядами окажутся бесполезными. С другой стороны, когда это произойдет, станут не нужны операции со старшими разрядами – необходимо улучшать точность решения поиском в младших разрядах. Такое «идеальное» поведение не обеспечивает семейство генетических алгоритмов с двоичным кодированием, т.к. эти алгоритмы оперируют битовой строкой целиком, и на первых же эпохах младшие разряды чисел "застывают", принимая случайное значение. В классических генетических алгоритмах разработаны специальные приемы по выходу из этой ситуации. Например, последовательный запуск ансамбля генетических алгоритмов с постепенным сужением пространства поиска.
Есть и другая проблема: при увеличении длины битовой строки необходимо увеличивать и численность популяции.
Математический аппарат непрерывных генетических алгоритмов
Как уже отмечалось, при работе с оптимизационными задачами в непрерывных пространствах вполне естественно представлять гены напрямую вещественными числами. В этом случае хромосома есть вектор вещественных чисел. Их точность будет определяться исключительно разрядной сеткой той ЭВМ, на которой реализуется real-coded алгоритм. Длина хромосомы будет совпадать с длиной вектора-решения оптимизационной задачи, иначе говоря, каждый ген будет отвечать за одну переменную. Генотип объекта становится идентичным его фенотипу.
Вышесказанное определяет список основных преимуществ алгоритмов с непрерывными генами:
Использование непрерывных генов делает возможным поиск в больших пространствах (даже в неизвестных), что трудно делать в случае двоичных генов, когда увеличение пространства поиска сокращает точность решения при неизменной длине хромосомы.
Одной из важных черт непрерывных генетических алгоритмов является их способность к локальной настройке решений.
Использование непрерывных генетических алгоритмов для представления решений удобно, поскольку близко к постановке большинства прикладных задач. Кроме того, отсутствие операций кодирования/декодирования, которые необходимы в генетических алгоритмах с двоичным кодированием, повышает скорость работы алгоритма.
Как известно, появление новых особей в популяции канонического генетического алгоритма обеспечивают несколько биологических операторов: отбор, скрещивание и мутация. В качестве операторов отбора особей в родительскую пару здесь подходят любые известные из двоичных генетических алгоритмов: рулетка, турнирный, случайный. Однако операторы скрещивания и мутации не годятся: в классических реализациях они работают с битовыми строками. Нужны собственные реализации, учитывающие специфику real-coded алгоритмов.
Оператор скрещивания непрерывного генетического алгоритма, или кроссовер, порождает одного или нескольких потомков от двух хромосом. Собственно говоря, требуется из двух векторов вещественных чисел получить новые векторы по каким-либо законам. Большинство real-coded алгоритмов генерируют новые векторы в окрестности родительских пар. Для начала рассмотрим простые и популярные кроссоверы.
Пусть 
и 
– две хромосомы, выбранные оператором селекции для скрещивания. После формулы для некоторых кроссоверов приводится рисунок – геометрическая интерпретация его работы. Предполагается, что 
и 
.
Плоский кроссовер (flat crossover): создается потомок 
– случайное число из интервала 
.
Простейший кроссовер (simple crossover): случайным образом выбирается число k из интервала 
и генерируются два потомка 
и 
.
Арифметический кроссовер (arithmetical crossover): создаются два потомка 
, 
, где 
, 
, 
, w либо константа (равномерный арифметический кроссовер) из интервала 
, либо изменяется с увеличением эпох (неравномерный арифметический кроссовер).
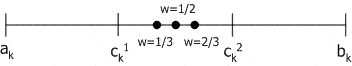
Геометрический кроссовер (geometrical crossover): создаются два потомка , , где 
, 
, w – случайное число из интервала .
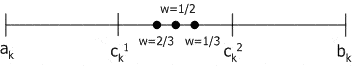
Смешанный кроссовер (blend, BLX-alpha crossover): генерируется один потомок 
, где 
– случайное число из интервала 
, 
, 
, 
. BLX-0.0 кроссовер превращается в плоский.
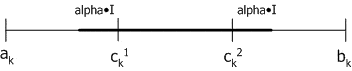
Линейный кроссовер (linear crossover): создаются три потомка 
, 
, где 
, 
, 
. На этапе селекции в этом кроссовере отбираются два наиболее сильных потомка.
Дискретный кроссовер (discrete crossover): каждый ген выбирается случайно по равномерному закону из конечного множества 
.
Расширенный линейчатый кроссовер (extended line crossover): ген 
, w – случайное число из интервала 
.
Эвристический кроссовер (Wright’s heuristic crossover). Пусть 
– один из двух родителей с лучшей приспособленностью. Тогда 
, w – случайное число из интервала 
.
Нечеткий кроссовер (fuzzy recombination, FR-d crossover): создаются два потомка , 
. Вероятность того, что в i-том гене появится число 
, задается распределением 
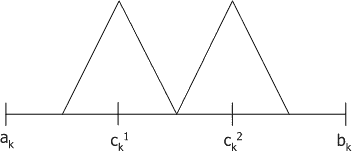
, где 
– распределения вероятностей треугольной формы (треугольные нечеткие функции принадлежности) со следующими свойствами 
( и 
):
| Распределение вероятностей | Минимум | Центр | Максимум |
|
|
|
|
|
|
|
|
|
|
Параметр d определяет степень перекрытия треугольных функций принадлежности, по умолчанию 
.
В качестве оператора мутации наибольшее распространение получили: случайная и неравномерная мутация (random and non-uniform mutation).
При случайной мутации ген, подлежащий изменению, принимает случайное значение из интервала своего изменения. В неравномерной мутации значение гена после оператора мутации рассчитывается по формуле:
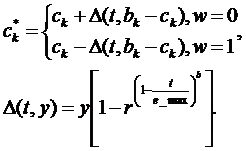
Сложно сказать, что более эффективно в каждом конкретном случае, но многочисленные исследования доказывают, что непрерывные генетические алгоритмы не менее эффективно, а часто гораздо эффективнее справляются с задачами оптимизации в многомерных пространствах, при этом более просты в реализации из-за отсутствия процедур кодирования и декодирования хромосом.
Рассмотренные кроссоверы исторически были предложены первыми, однако во многих задачах их эффективность оказывается невысокой. Исключение составляет BLX-кроссовер с параметром 
– он превосходит по эффективности большинство простых кроссоверов. Позднее были разработаны улучшенные операторы скрещивания, аналитическая формула которых и эффективность обоснованы теоретически. Рассмотрим подробнее один из таких кроссоверов – SBX.
SBX (англ.: Simulated Binary Crossover) – кроссовер, имитирующий двоичный. Был разработан в 1995 году исследовательской группой под руководством K. Deb’а. Как следует из его названия, этот кроссовер моделирует принципы работы двоичного оператора скрещивания.
SBX кроссовер был получен следующим способом. У двоичного кроссовера было обнаружено важное свойство – среднее значение функции приспособленности оставалось неизменным у родителей и их потомков, полученных путем скрещивания. Затем автором было введено понятие силы поиска кроссовера (search power). Это количественная величина, характеризующая распределение вероятностей появления любого потомка от двух произвольных родителей. Первоначально была рассчитана сила поиска для одноточечного двоичного кроссовера, а затем был разработан вещественный SBX кроссовер с такой же силой поиска. В нем сила поиска характеризуется распределением вероятностей случайной величины 
:
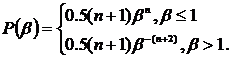
Для генерации потомков используется следующий алгоритм, использующий выражение для 
. Создаются два потомка 
, 
, где 
, 
– число, полученное по формуле:
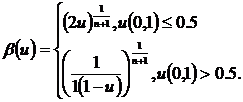
В формуле 
– случайное число, распределенное по равномерному закону, 
– параметр кроссовера.
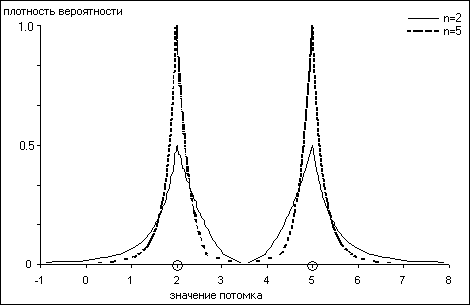
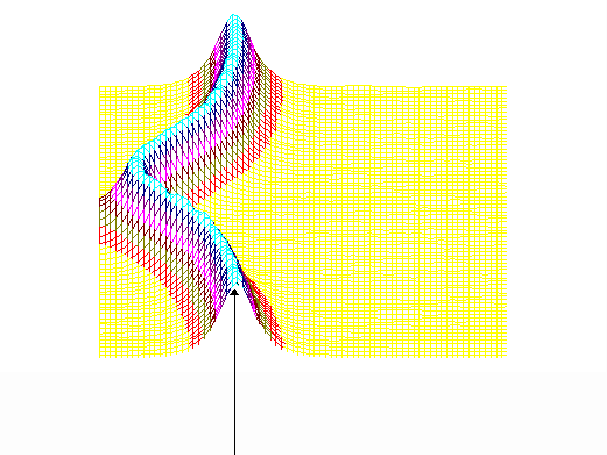
На рисунке приведена геометрическая интерпретация работы SBX кроссовера при скрещивании двух хромосом, соответствующих вещественным числам 2 и 5. Видно, как параметр n влияет на конечный результат: увеличение n влечет за собой увеличение вероятности появления потомка в окрестности родителя и наоборот.
Эксперименты автора SBX кроссовера показали, что он во многих случаях эффективнее BLX, хотя, очевидно, что не существует ни одного кроссовера, эффективного во всех случаях. Исследования показывают, что использование нескольких различных операторов кроссовера позволяет уменьшить вероятность преждевременной сходимости, т.е. улучшить эффективность алгоритма оптимизации в целом. Для этого могут использоваться специальные стратегии, изменяющие вероятность применения отдельного эволюционного оператора в зависимости от его «успешности», или использование гибридных кроссоверов, которых в настоящее время насчитывается несколько десятков. В любом случае, если перед Вами стоит задача оптимизации в непрерывных пространствах, и Вы планируете применить эволюционные техники, то следует сделать выбор в пользу непрерывного генетического алгоритма.
4. Заключение
За последние годы объёмы экономической информации возросли в несколько раз, и это является дополнительным стимулом для многих учёных, работающих в области анализа данных, теории информации и теории алгоритмов, заниматься генетическими алгоритмами.
Очевидно, этим объясняется появление статей по данной теме и на русском языке (на других языках уже опубликовано 9000 работ). Правда, стоит отметить, что пока многие публикации частично (в большей или меньшей степени) повторяют друг друга и может создаться ложное представление о том, что теория генетических алгоритмов и, в частности, такая её часть, как непрерывные генетические алгоритмы, – тема узкая и исчерпываемая двадцатью страницами данной работы. На самом же деле есть не только теория, но и практика генетических алгоритмов. В настоящее время известно о существовании более пятисот программных продуктов, в том или ином виде использующих генетические алгоритмы для решения оптимизационных и прогностических задача.
Также стоит отметить, что талантливые программисты создали популярную игру, базирующуюся на наработках теории генетических алгоритмов, которая называется «Амёбы: Борьба видов» (http://amebas.ru). Суть игры заключается в том, что каждый игрок «выращивает» на своём компьютере колонию амёб. Каждая амёба имеет свой генотип и ведёт борьбу за выживание. В каждом поколении в ходе сражений часть из них остаётся в проигрыше и не получает возможности размножаться. По ходу развития (с каждым следующим поколением) амёбы накапливают в себе всё больше и больше генетической информации. Раз в некоторое время проводятся Интернет-турниры, на которые каждый игрок выставляет свою лучшую амёбу. В игре учитываются разные возможности скрещивания, возможность направить отбор в том или ином направлении, регулировка количества и силы мутаций и прочие настройки.
В заключение можно сказать, что мои прогнозы развития генетических алгоритмов являются очень оптимистичными по двум причинам:
С повышением вычислительной мощности ЭВМ (не исключено, что после перехода на квантовые или молекулярные компьютеры) станет возможным моделировать при помощи генетических алгоритмов всё более и более сложные ситуации.
Не исключено, что учёные, работающие в области классической теории алгоритмов, найдут решение одной из NP-полных задач, и тогда окажутся решаемыми все алгоритмы, относящиеся к сложности NP.
Список литературы«АНАЛИТИЧЕСКИЕ ТЕХНОЛОГИИ для прогнозирования и анализа данных», 2005. «НейроПроект»
http://www.gotai.ru
http://basegroup.ru
http://ru.wikipedia
Похожие работы
... решения Скрещивание, рекомбинация, кроссинговер Оператор рекомбинации мутация Оператор модификации При разработке генетических алгоритмов преследуется две главные цели: · Абстрактное и формальное объяснение процессов адаптации в естественных системах; · Проектирование искусственных программных систем, воспроизводящих механизмы функционирования естественных систем. Основные отличия ГА от ...
... Таким образом, с помощью ГА удалось создать очень хорошую микрополосковую конструкцию. V. Прореженные подрешетки генетический алгоритм хромосомы Большие антенны с фазированными решетками строить весьма накладно. Если делить решетки на подрешетки, можно получить выигрыш в затратах на расчет, сооружение и обслуживание большой решетки. Если амплитудное и/или фазовое взвешивание выполнять не на ...
... что при такой ориентации теста знания у сильных и слабых испытуемых измерялись с меньшей точностью. 3) Автоматизированный контроль знаний с применением компьютера и обработка результатов тестирования на ЭВМ для определения параметров качества тестирования. 2.1.9.4 Блок адаптивного обучения 1) Модели обучения. Информационные технологии оказывают решающее влияние на все этапы процесса обучения: ...
... геномах растений, вызываемые с помощью ФПУ-трансформированной человеческой речи, которая резонансно взаимодействует с хромосомной ДНК in vivo [25,29]. Этот результат, осмысленный нами с позиций семиотико-волновой составляющей генетического кода, имеет существенное методологическое значение и для анализа таких суперзнаковых объектов, как тексты ДНК, и для генома в целом. Открываются принципиально ...
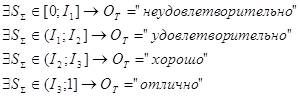
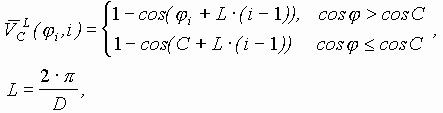
0 комментариев