Навигация
3. Дальше в лес
Оказывается, из (σ′1) можно вывести, что
| s0 < 55. | (3) |
В самом деле, предположим, что s0 ≥ 55. Тогда s0 не обладает свойством (σ′1): можно так разложить его в сумму двух слагаемых, удовлетворяющих неравенствам (1), что для их произведения не будет выполнено условие (π′1). Это разложение: s0 = (s0 – 53) + 53. Из s0 ≥ 55 вытекает s0 – 53 ≥ 2. Произведение (s0–53)·53 единственным образом разлагается на два множителя, сумма которых меньше ста: поскольку 53 – простое число, один из множителей обязательно имеет вид 53d; так как 53·2 > 100, d = 1. Но по условию s0 обладает свойством (σ′1). Противоречие!
После (3) для s0 остается уже 11 возможностей:
| 11, 17, 23, 27, 29, 35, 37, 41, 47, 51, 53. | (4) |
Попробуем теперь без перебора установить, какие из чисел (4) удовлетворяют условию (σ′1). Пусть s – произвольное из чисел (4). Поскольку s нечётно, всякое его разложение в сумму имеет вид s = 2а + m. Допустим, s не обладает свойством (σ′1). Тогда найдётся такое а, что произведение 2a·m «расшифровывается» однозначно.
Это a не может равняться единице, так как в этом случае s = 2 + m, а произведение 2m двояко разлагается в произведение. В самом деле, поскольку m = s–2 – составное нечётное число, m = pq, где р > 2 и q > 2. Оба разложения
2m = 2·pq = 2p·q
годятся: 2 + pq = 2 + m = s < 100 и 2p + q = 2 + pq – (p – 1)(q – 2) < 2 + pq < 100.
Значит, a ≥ 2.
Если a ≠ m, то 2a·m и 2m·a – два различных разложения. Поскольку 2a + m = s < 100 и s не обладает свойством (σ′1), должно быть 2m + a ≥ 100. Так как s = 2a + m ≤ 53, имеем m ≤ 53 – 2a, 2m + a ≤ 106 – 3a. Из 2m + a ≥ 100 и 2m + a ≤ 106 – 3a вытекает a ≤ 2. Следовательно, a = 2. Из 2m + a ≥ 100 и m ≤ 53 – 2a получаем теперь m = 49. Итак, в этом случае s = 53, причём «подозрительным» является разложение 53 = 4 + 49.
Если же a = m, то s = 3a делится на 3. В (4) таких чисел два: 27 и 51. «Подозрительными» являются разложения 27 = 9 + 18 и 51 = 17 + 34.
Число 51 действительно не обладает свойством (σ′1): 51 = 17 + 34, и произведение 17·34 при разложении на два множителя даёт только одну сумму, меньшую ста. Таким образом, его можно выбросить из списка «кандидатов в s0».
Числа 27 и 53 удовлетворяют условию (σ′1): 9·18 = 2·81 и 2 + 81 < 100; 4·49 = 7·28 и 7 + 28 < 100.
Итак, для дальнейшего исследования осталось 10 кандидатов: 11, 17, 23, 27, 29, 35, 37, 41, 47, 53, причём все они обладают свойством (σ′1).
4. «Тогда и я их знаю»
Используем, наконец, (π2) и (σ2).
Можно было бы истолковать (π2) и (σ2) подобно тому, как мы это сделали с (π1) и (σ1). Мы попробуем обойтись без этого.
Из (σ2) и (3) можно вывести
| s0 < 33. | (5) |
Допустим противное: s0 ≥ 33. Тогда математик S, разлагая всеми возможными способами s0 в сумму двух слагаемых, имел бы среди этих разложений s0 = (s0 – 31) + 31 = (s0 – 29) + 29.
Если бы P было сообщено произведение (s0–31)·31, то он мог бы, сообразив (3) и учтя, что 31 – простое число, понять, что (s0–31)·31 единственным образом разлагается в произведение двух множителей, сумма которых удовлетворяет (3). В этом случае P отгадал бы k0 и l0.
Аналогичная возможность была у P, если ему было сообщено произведение (s0–29)·29,.
Значит, в случае s0 ≥ 33, S и после (π2) не смог бы точно назвать k0, l0, т.е. не смог бы произнести (σ2).
После (5) остается 5 кандидатов: 11, 17, 23, 27, 29.
Если p0 имеет вид 2n·p, где p – нечётное простое число, то P однозначно определяет k0 и l0, потому что из всех сумм 2n–t + 2tp нечётна только одна: 2n + p. Поэтому, если s0 двумя способами представимо в виде 2n + p, то S опять-таки не может произнести (σ2).
Это соображение позволяет отсеять ещё 3 кандидата: 11 = 4 + 7 = 8 + 3, 23 и 27.
Остались 2 кандидата: 17 и 29.
5. Тогда и мы их знаем
29 тоже не годится, поскольку 29 = 4 + 25 = 16 + 13: если бы P имел p0 = 16·13, он бы отгадал k0 и l0, так как среди сумм 24–t + 2t·13 нечётна только одна; если бы P имел p0 = 4·25, он бы тоже отгадал k0 и l0: среди соответствующих сумм нечётна, кроме 29, ещё только 25 (4·25 = 5·20), но 25–2 – простое число.
Итак, либо s0 = 17, либо задача не имеет решений.
Какое же p0 могло быть у P при s0 = 17? Переберём все разложения числа 17 в сумму двух слагаемых:
17 = 2 + 15 = 3 + 14 = ... = 8 + 9.
При любом из произведений, кроме 4·13, P не смог бы произнести (π2). Например, если бы P имел p0 = 30, он среди разложений числа 30 в произведение двух множителей увидел бы и 30 = 2·15, и 30 = 5·6, но как 17, так и 11 обладают свойством (σ′1).
Остается единственный кандидат для p0: 52. Этот кандидат дает возможность P произнести (π2): среди всех разложений числа 52 в произведение двух множителей существует ровно одно: 52 = 4·13, дающее нечётную сумму.
Итак, s0 = 17, p0 = 52, k0 = 4, l0 =
Похожие работы
... новую песню?) Yes, I will (да, приду, да, буду, да сделаю). Не то чтобы will сдавал позиции. Просто come и gonna отвоевывают позиции под лучами англоязычного солнца. Конечно, об активном разговорном American English — языке общаг, кухонь, "Макдональдсов", спортивных площадок, колледжей и казарм — можно говорить еще и еще, но, как выражаются американцы: next time — как-нибудь в следующий раз. ...
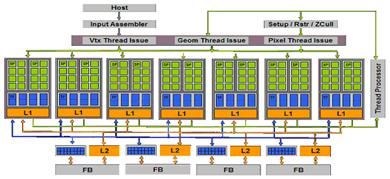
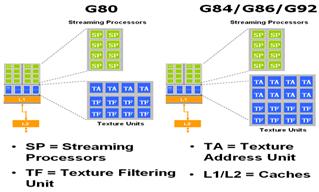
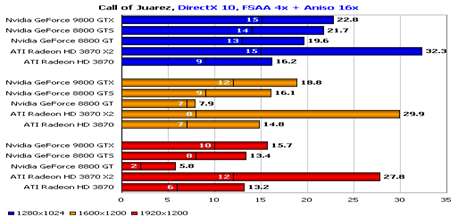
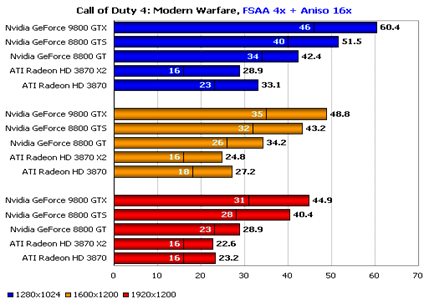
... решения Bliss 9800 GTX 512MB мы не имеем. 3. Экономический расчет стоимости анализа обьекта Целью экономического расчета дипломного проекта является выбор оптимальной видеокарты для дизайнерского моделирования ООО "Бест Вей корп.", качественная и количественная оценка экономической целесообразности создания, использования и развития этой видеокарты, а также определение организационно- ...
... не за один день построен. Ср. Не сразу Москва строилась. Не вдруг все делается. 719. Salt water and absence wash away love. Любовь пропадает во время долгого плавания. Ср. С глаз долой — из сердца вон. 720. Saying and doing are two things. Сказать и сделать — две разные вещи. Ср. Скоро только говорится, а не скоро дело делается. Сказано — не доказано, надо сделать. От слова до дела — бабушкина ...
... . Замена привлекает внимание созвучием исходного и заменяющего компонентов. Заголовок - это способ дать читателю возможность с первого взгляда сориентироваться, нужно ли читать остальной текст. Трансформация фразеологизма обусловлена стремлением авторов усилить экспрессивную окраску заголовка. Мы выяснили, что такое изменение фразеологизмов служит «противоядием» от речевых штампов. Преобразуя ...


0 комментариев