Предел.
Число А наз-ся пределом последоват-ти Xn если для любого числа Е>0, сколь угодно малого, $ N0, такое что при всех n>N0 будет выполн-ся нер-во |Xn-A|N2 |Xn-и|N0. |a-b|=|a-Xn+Xn-b|£|a-Xn|+|Xn-b| |a-b|=0 => a=b.
2.теорема о сжатой переменной. n>N1 Xn³Zn³Yn $ limXn = lim Yn = a (n®¥) => $ lim Zn=a (n®¥)
Док-во: 1. из того, что $ lim Xn=a (n®¥) => n>N2 |Xn-a|a-E => lim Zn=a (n®¥)
Функция y=f(x) наз-ся ограниченной в данной обл-ти изменения аргумента Х, если сущ-ет положит число М такое, что для всех значений Х, принадлежащих рассматриваемой обл-ти, будет выполн-ся нер-во |f(x)|£M. Если же такого числа М не сущ-ет, то f(x) наз-ся неограниченной в данной обл-ти.
Бесконечно малая величина.
Величина Xn наз-ся бесконечно малой при n®¥, если lim Xn = 0 (n®¥). "E>0, N0, n>N0, |Xn| " E/2 $N1, n>N1 |Xn|" E/2 $N2, n>N2 |Yn|N0, |Xn±Yn|£|Xn|+|Yn| lim(Xn±Yn)=0 (n®¥). Теорема справедлива для любого конечного числа б.м. слагаемых.
2.Произведение ограниченной величины на б.м. величину есть величина б.м.
Док-во:Xn – огр. величина => $ K, |Xn| £ K,
Yn – б.м. => " E/K $N0 n>N0 |Yn| "E $N0 n>N0 |Xn-a| Xn=a+Yn. Справедливо и обратное: если переменную величину можно представить в виде суммы Xn=a+Yn (Yn – б.м.), то lim Xn=a (n®¥).
Бесконечно большая величина
Xn – бесконечно большая n®¥, если "M>0 $N0, n>N0, |Xn|>M => MN2 |Yn|>M
N0=max(N1, N2) => |Xn*Yn|=|Xn||Yn|>MM=M2>M
Lim XnYn=¥ (n®¥).
2.Обратная величина б.м. есть б.б. Обратная величина б.б. есть б.м. lim Xn=¥ (n®¥) – б.б. Yn=1/Xn – б.м. Из lim Xn=¥ => M=1/E $N0, n>N0 |Xn|>M =>n>N0.
|Yn|=1/|Xn|Yn – б.м. => lim Yn=0 (n®¥).
3.Сумма б.б величины и ограниченной есть б.б. величина.
Основные теоремы о пределах:
lim Xn=a, lim Yn=b => lim (Xn±Yn)=a±b (n®¥)
Док-во: lim Xn=a => Xn=a+an; lim Yn=b => Yn=b+bn;
Xn ± Yn = (a + an) ± (b + bn) = (a ± b) + (a n± bn) => lim(Xn±Yn)=a±b (n®¥).
limXnYn = lim Xn * lim Yn (n®¥).
lim Xn=a, lim Yn=b (n®¥) => lim Xn/Yn =
(lim Xn)/(lim Yn) = a/b.
Док-во: Xn/Yn – a/b = (a+an)/(b+bn) – a/b = (ab+anb–ab–abn)/b(b+bn) =(ban-abn)/b(b+bn)=gn => Xn/Yn=a/b+gn => $ lim Xn/Yn = a/b = (lim Xn)/(lim Yn) (n®¥).
Пределы ф-ии непрерывного аргумента.
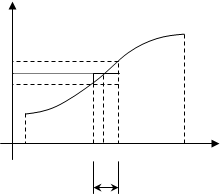
Число А наз-ся пределом ф-ии y=f(x) при х®x0, если для любого Е>0 сколь угодно малого сущ-ет такое число d>0, что при "x будет выпол |x-x0|0 сколь угодно большого $ d>0, что "x |x-x0|M, "x x0-dM.
Lim f(x)=¥ (x®x0).
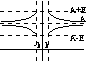 Число А наз-ся пределом y=f(x) x®¥, если для любого Е>0 можно найти число К, "x |x|>K |f(x)-A|
Число А наз-ся пределом y=f(x) x®¥, если для любого Е>0 можно найти число К, "x |x|>K |f(x)-A|
Похожие работы
... наибольших, наименьших значений функций. 4. Нахождения дифференциала для приближенных вычислений. 5. Для доказательства неравенств. Рассмотрю некоторые примеры применения производной в алгебре, геометрии и физике. Задача 1. Найти сумму 1+2*1/3+3(1/3)2+…+100(1/3)99; Решение. Найду сумму g(x)=1+2x+3x2+…+100x99 и подставлю в нее x=1/3. Для этого потребуется ...
ывают определением на «языке последовательностей». Второе определение носит название «на языке ». Кроме понятия предела функции в точке, существует также понятие предела функции при стремлении аргумента к бесконечности: число А называется пределом функции при , если для любого числа существует такое число d, что при всех справедливо неравенство : . Теоремы о пределах функций являются базой для ...
... предел функции Решение: Имеем неопределенность вида . Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель , который при не равен нулю. В результате неопределенность будет раскрыта. 2. Производная и дифференциал Пусть функция определена в некоторой окрестности точки . Производной функции в точке называется предел отношения , когда ( ...
... по алгебре и началам анализа, при подготовке к государственной итоговой аттестации, внешнему независимому оцениванию. Достаточно большое число задач раскрывают потенциальные возможности анализа бесконечно малых величин. 1. Производная и ее применение для решения прикладных задач 1.1 Исторические сведения Ряд задач дифференциального исчисления был решен еще в древности. Они встречались у ...

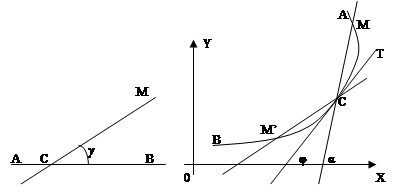





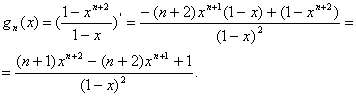
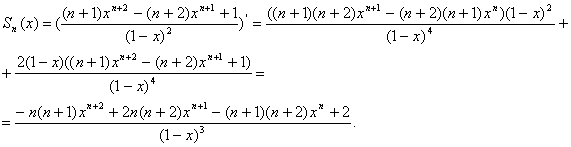

0 комментариев